2008年福建省宁德市中考数学真题及答案.doc-资料库

第1页 / 共11页

第2页 / 共11页

第3页 / 共11页

第4页 / 共11页

第5页 / 共11页

第6页 / 共11页

第7页 / 共11页

第8页 / 共11页

2008 年福建省宁德市中考数学真题及答案 [参考公式：抛物线 y  2 ax  bx   ac  0 的顶点坐标为     b 2 a 4 ， ac  4 a 2 b    ，对称轴 x  b 2 a ] 一、选择题（本大题有 10 小题，每小题 4 分，共 40 分） 1.下列各数中，最小的实数是（）． A.－3 B.－1 C.0 D. 3 2.宁德市位于福建省东北部，有漫长的海岸线.据测算，海岸线总长约为 878000 米，用科学记数法表示这个数为（）． A.0.878×106 米 B.8.78×106 米 C.878×103 米 D.8.78×105 米 3.如图，已知 AB∥CD，∠A＝70°，则∠1 度数是（）． A.70° B.100° C.110° D.130° 4.小明五次立定跳远的成绩（单位：米）是：2.3，2.2，2.1，2.3， 2.0．这组数据的众数是（）． A．2.2 米 B．2.3 米 C．2.18 米 D．0.3 米 C A 1 第 3 题图 D B 5.不等式 5 2 x＜ A. 25 0 x＞ 的解集是（）． 2 5 5 x＞ 2 x＜ B. C. D. x＜ 5 2 6.如图，国际奥委会会旗上的图案是由五个圆环组成，在这个图案中反映出的两圆位置关系有（）． A.内切、相交 B.外离、相交 C.外切、外离 D.外离、内切 7.向如图所示的盘中随机抛掷一枚骰子，落在阴影区域的概率（盘底被等分成 12 份，不考虑骰子落在线上情形）是（）． A. 1 6 B. 1 4 C. 1 3 D. 1 2 8.如图所示零件的左视图是（）．第 6 题图第 7 题图正面 A. B. C. D. 第 8 题图 9.如果 x＝4 是一元二次方程 2 x  3 x  2 a 的一个根，那么常数 a的值是（）． A.2 B.－2 C.±2 D.±4

10.如图，点 A 的坐标是（1，1），若点 B 在 x 轴上，且△ABO 是等腰三角形，则点 B 的坐标不可能．．．是（）． A.（2，0） B.（ 1 2 ，0） C.（ 2 ，0） D.（1，0）二、填空题（本大题有 8 小题，每小题 3 分，共 24 分） 11.计算： 12 ________________. 12.计算： 3 m6   m3 2 ＝________________. 13.因式分解: 2 x 9 ＝ ________________. A B y 1 O -1 A 1 2 x 第 10 题图 D E 第 14 题图 C 14.如图是一副三角尺拼成图案，则∠AEB＝_________°. 15.蓄电池电压为定值，使用此电源时，电流 I（安）与电阻 R（欧） I（安）之间关系图象如图所示，若点 P 在图象上，则 I 与 R（R＞0）的函数关 ·P（3，12）系式是______________． O 第 15 题图 R（欧） 16.如图，PA 切半圆 O 于 A 点，如果∠P＝35°，那么∠AOP＝_____°. 17.用卡片进行有理数加法训练，李明手中的三张卡片分别是 3、－1、 A －2，刘华手中的三张卡片分别是 2、0、－1．如果每人随机抽取一张卡片，则和为正数的概率是__________. O 第 16 题图 P 18.如图，将矩形纸 ABCD 的四个角向内折起，恰好拼成一个无缝隙无 A H 重叠的四边形 EFGH，若 EH＝3 厘米，EF＝4 厘米，则边 AD 的长是 ___________厘米. E B 三、解答题（本大题有 8 小题，共 86 分） 19．（本题满分 10 分）化简，求值： x（  )3 2  ( xx  )8 ，其中 x 42  ．解： D G F C 第 18 题图

20．（本题满分 10 分）如图，E 是□ABCD 的边 BA 延长线上一点，连接 EC，交 AD 于 F．在不添加辅助线的情况下，请找出图中的一对相似三角形，并说明理由．解： E A F D B C 21．（本题满分 10 分）“五一”期间，新华商场贴出促销海报，内容如图 1．在商场活动期间，王莉和同组同学随机调查了部分参与活动的顾客，统计了 200 人次的摸奖情况，绘制成如图 2 的频数分布直方图．人次 “五一”大派送为了回馈广大顾客，本商场在 4 月 30 日至 5 月 6 日期间举办有奖购物活动．每购买 100 元的商品，就有一次摸奖的机会，奖品为：一等奖：50 元购物券二等奖：20 元购物券三等奖：5 元购物券图 1 （1）补齐频数分布直方图；（2）求所调查的 200 人次摸奖的获奖率；（3）若商场每天约有 2000 人次摸奖，请估算商场一天送出的购物券总金额是多少元？图 2 购物券

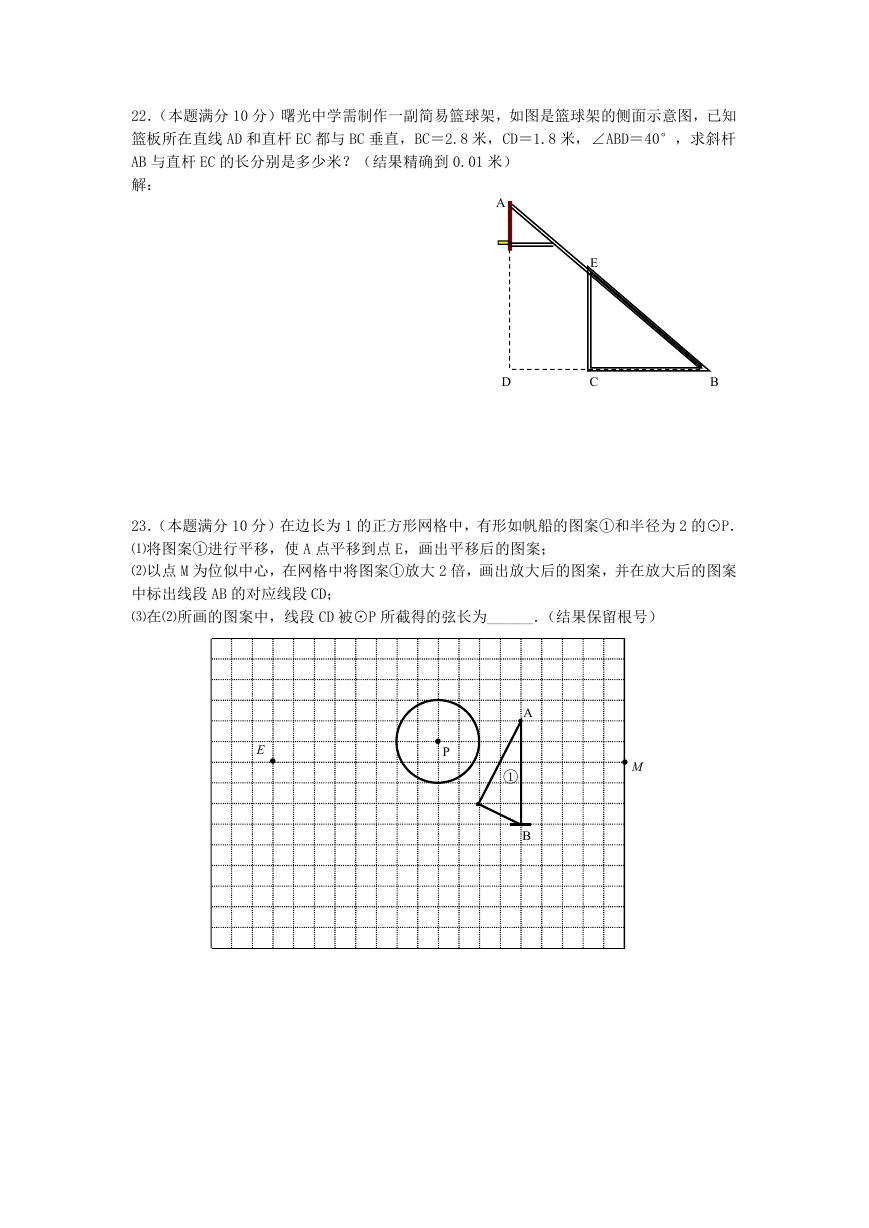
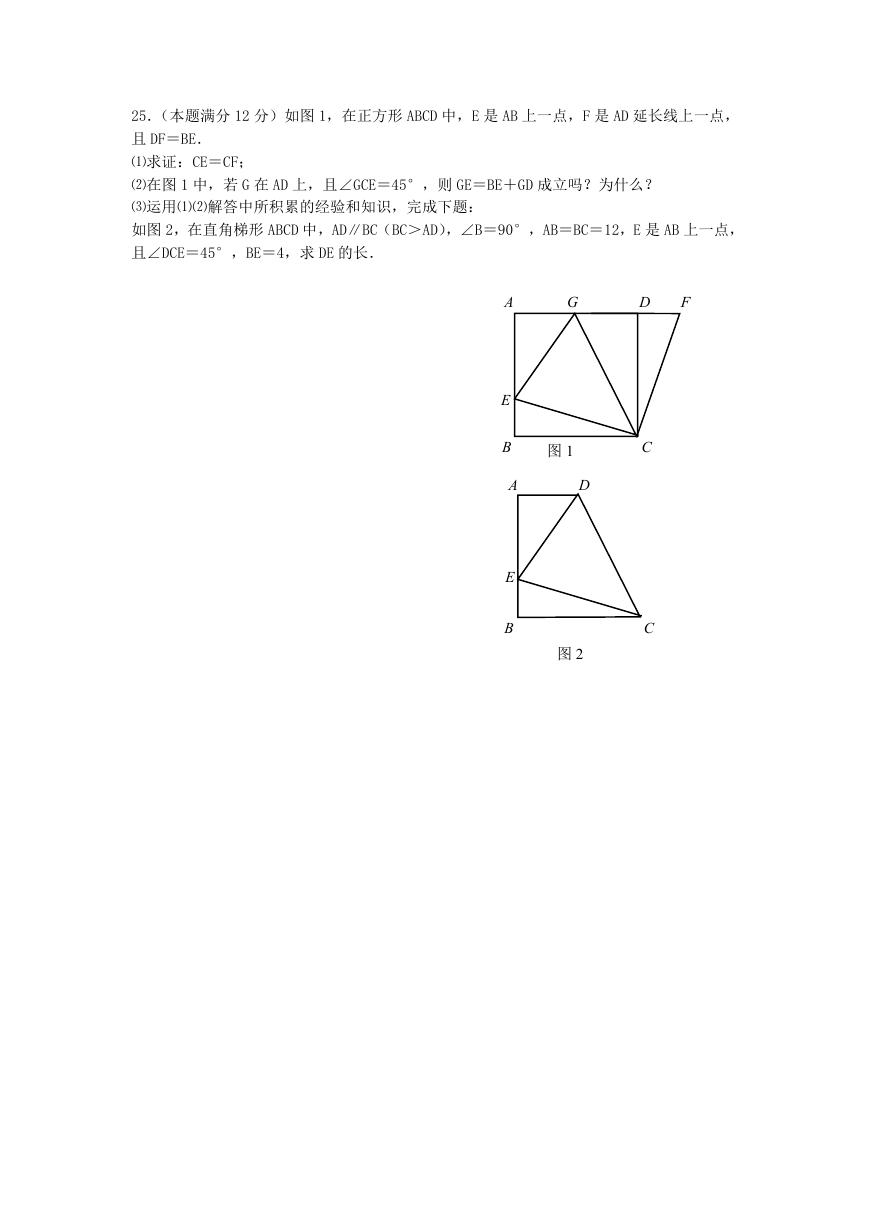
22．（本题满分 10 分）曙光中学需制作一副简易篮球架，如图是篮球架的侧面示意图，已知篮板所在直线 AD 和直杆 EC 都与 BC 垂直，BC＝2.8 米，CD＝1.8 米，∠ABD＝40°，求斜杆 AB 与直杆 EC 的长分别是多少米？（结果精确到 0.01 米）解： A D E C B 23．（本题满分 10 分）在边长为 1 的正方形网格中，有形如帆船的图案①和半径为 2 的⊙P． ⑴将图案①进行平移，使 A 点平移到点 E，画出平移后的图案； ⑵以点 M 为位似中心，在网格中将图案①放大 2 倍，画出放大后的图案，并在放大后的图案中标出线段 AB 的对应线段 CD； ⑶在⑵所画的图案中，线段 CD 被⊙P 所截得的弦长为______．（结果保留根号） E P ① A B M

24．（本题满分 10 分）5 月 12 日 14 时 28 分，四川汶川发生了 8.0 级大地震，震后两小时，武警某师参谋长王毅奉命率部队乘车火速向汶川县城开进．13 日凌晨 1 时 15 分，车行至古尔沟，巨大的山体塌方将道路完全堵塞，部队无法继续前进，王毅毅然决定带领先遣分队徒步向汶川挺进，到达理县时为救援当地受灾群众而耽误了 1 小时，随后，先遣分队将步行速度提高 1 9 ，于 13 日 23 时 15 分赶到汶川县城． ⑴设先遣分队从古尔沟到理县的步行平均速度为每小时 x 千米，请根据题意填写下表：时间（小时）速度（千米/小时） x 所走路程（千米）古尔沟到理县理县到汶川 30 60 ⑵根据题意及表中所得的信息列方程，并求出先遣分队徒步从理县到汶川的平均速度是每小时多少千米？

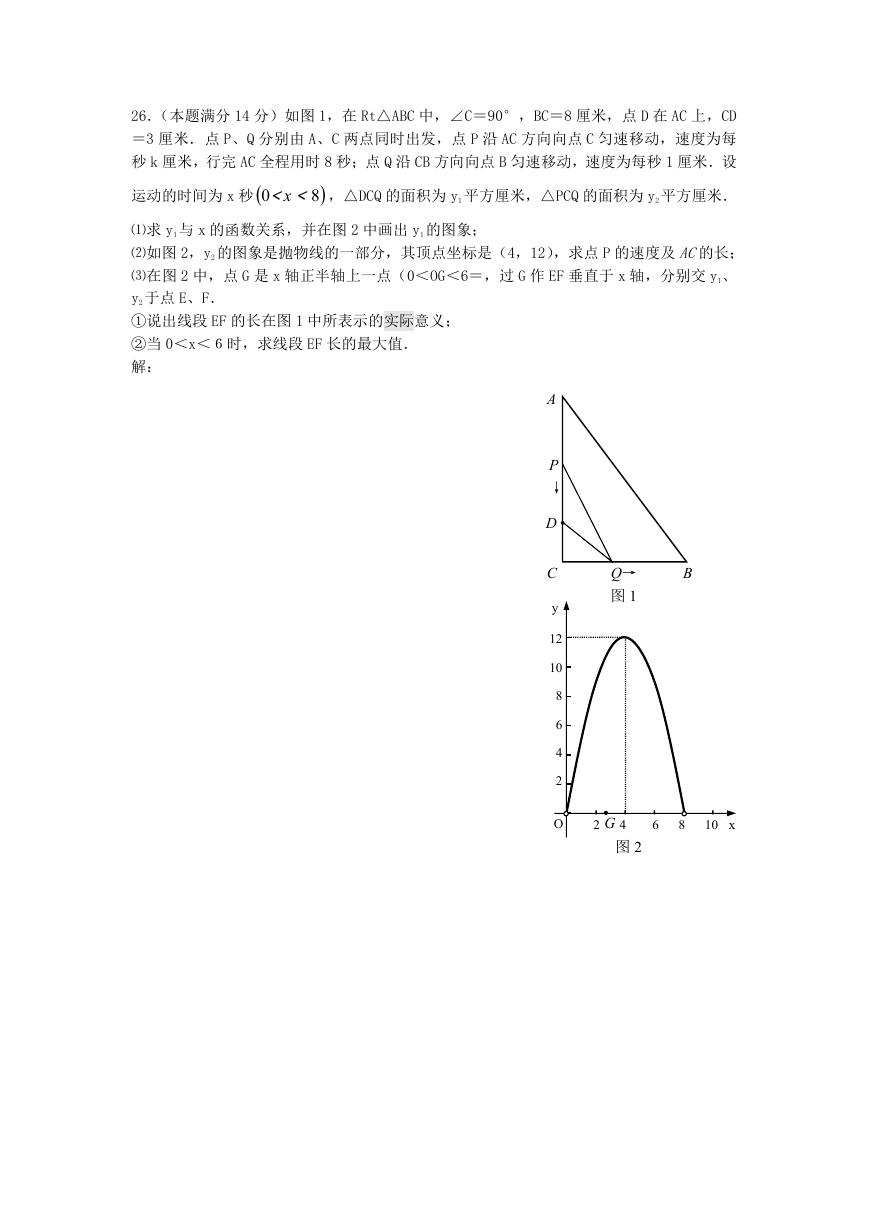
25．（本题满分 12 分）如图 1，在正方形 ABCD 中，E 是 AB 上一点，F 是 AD 延长线上一点，且 DF＝BE． ⑴求证：CE＝CF； ⑵在图 1 中，若 G 在 AD 上，且∠GCE＝45°，则 GE＝BE＋GD 成立吗？为什么？ ⑶运用⑴⑵解答中所积累的经验和知识，完成下题：如图 2，在直角梯形 ABCD 中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝12，E 是 AB 上一点，且∠DCE＝45°，BE＝4，求 DE 的长． A G D F E B A E B 图 1 D 图 2 C C

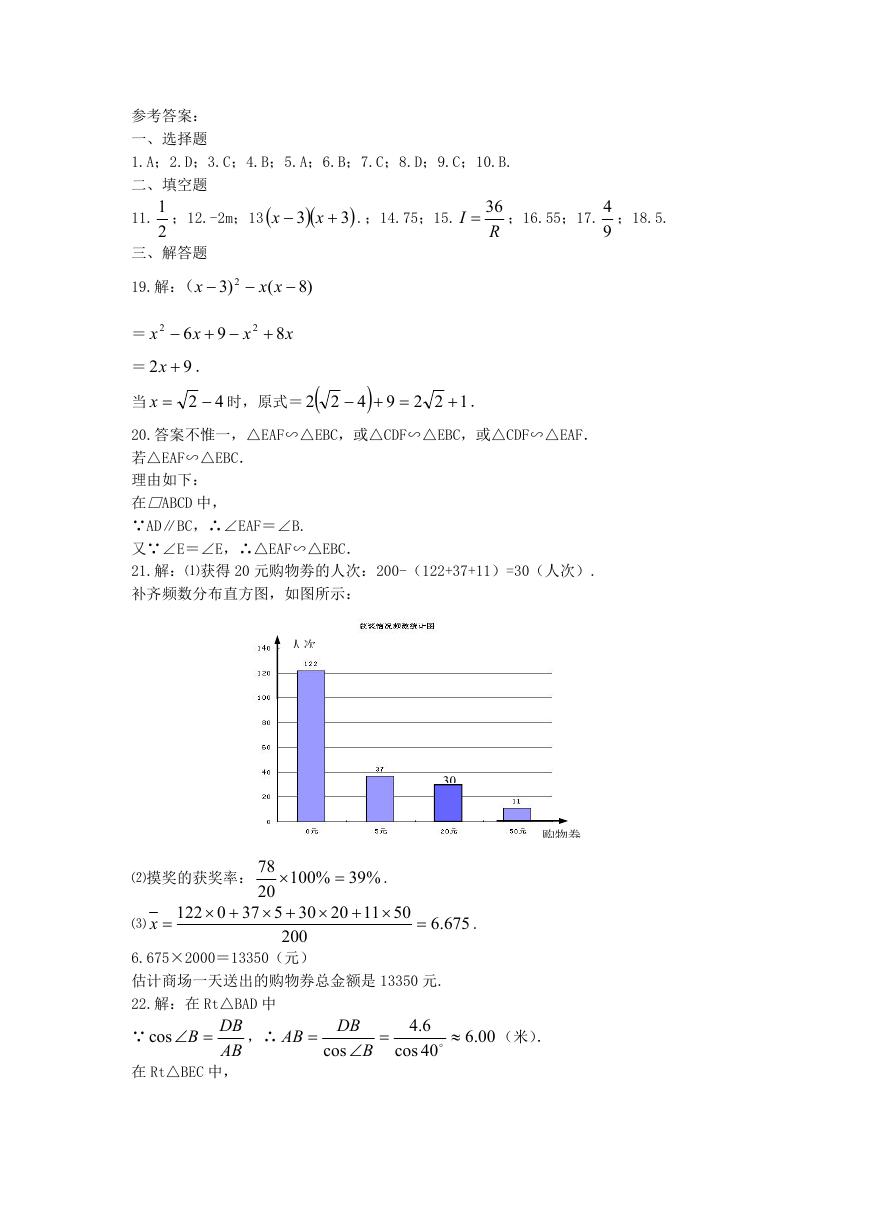
26．（本题满分 14 分）如图 1，在 Rt△ABC 中，∠C＝90°，BC＝8 厘米，点 D 在 AC 上，CD ＝3 厘米．点 P、Q 分别由 A、C 两点同时出发，点 P 沿 AC 方向向点 C 匀速移动，速度为每秒 k 厘米，行完 AC 全程用时 8 秒；点 Q 沿 CB 方向向点 B 匀速移动，速度为每秒 1 厘米．设运动的时间为 x 秒 0＜x＜，△DCQ 的面积为 y1 平方厘米，△PCQ 的面积为 y2 平方厘米． 8 ⑴求 y1 与 x 的函数关系，并在图 2 中画出 y1 的图象； ⑵如图 2，y2 的图象是抛物线的一部分，其顶点坐标是（4，12），求点 P 的速度及 AC的长； ⑶在图 2 中，点 G 是 x 轴正半轴上一点（0＜OG＜6＝，过 G 作 EF 垂直于 x 轴，分别交 y1、 y2 于点 E、F． ①说出线段 EF 的长在图 1 中所表示的实际意义； ②当 0＜x＜６时，求线段 EF 长的最大值．解： A P ↓ D C y 12 10 8 6 4 2 O Q→ 图 1 B 6 8 10 x G2 4 图 2

参考答案：一、选择题 1.A；2.D；3.C；4.B；5.A；6.B；7.C；8.D；9.C；10.B. 二、填空题 11. 1 2 ；12.-2m；13 x  3 x   3 .；14.75；15. I 36 ；16.55；17. R 4 9 ；18.5. 三、解答题 19.解： x（  )3 2  ( xx  )8  9 2 x  8 x ＝＝当 2  6 x x 9 2 x ． 2  x 时，原式＝  22 4   4  9 122  ． 20.答案不惟一，△EAF∽△EBC，或△CDF∽△EBC，或△CDF∽△EAF．若△EAF∽△EBC．理由如下：在□ABCD 中， ∵AD∥BC，∴∠EAF＝∠B. 又∵∠E＝∠E，∴△EAF∽△EBC． 21.解：⑴获得 20 元购物劵的人次：200-（122+37+11）=30（人次）. 补齐频数分布直方图，如图所示：人次 30 购物券   0 ⑶ 37 x 122  ⑵摸奖的获奖率： 78 %39%100 20 5 30 11  200 6.675×2000＝13350（元）估计商场一天送出的购物券总金额是 13350 元. 22.解：在 Rt△BAD 中 50 20 .   .6 675 .   ∵ B cos DB AB 在 Rt△BEC 中，，∴ AB  DB  cos B  6.4 40 cos   00.6 （米）．

资料库

2008年福建省宁德市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料