logo资料库

一级倒立摆系统.docx

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：0.21M 资料格式：docx 举报 版权申诉
第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
资料共14页，剩余部分请下载后查看
    《现代控制理论》三级项目报告 题目：一级倒立摆控制系统设计 姓 学 专 名： 刘会林 号： 150102020027 业： 15 级工自 4 班 指导教师： 张秀玲 分 数：
    一级倒立摆控制系统设计 一级倒立摆控制系统设计 刘会林 （燕山大学 电气工程学院） 摘要：本文通过对倒立摆进行建模分析，将倒立摆类比为小车和摆杆的简单模型， 首先运用牛顿运动定律建立倒立摆系统的运动方程，进而求出系统的状态空间表 达式，建立数学模型。再通过对系统进行稳定性分析，并运用 simulink 对系统 进行仿真，其次利用 matlab 对系统的能控性、能观性进行定性分析；通过运用 状态反馈极点配置法，以小车的位移、速度，摆杆与竖直向上的偏角、摆角变化 速度作为四个状态变量，由系统稳定性的要求求出状态反馈增益矩阵，将极点配 置在为系统稳定的范围内；另外考虑到系统的某些状态不容易直接测量，本文通 过建立全维观测器，对状态进行了重构并给出了仿真结果分析。 1
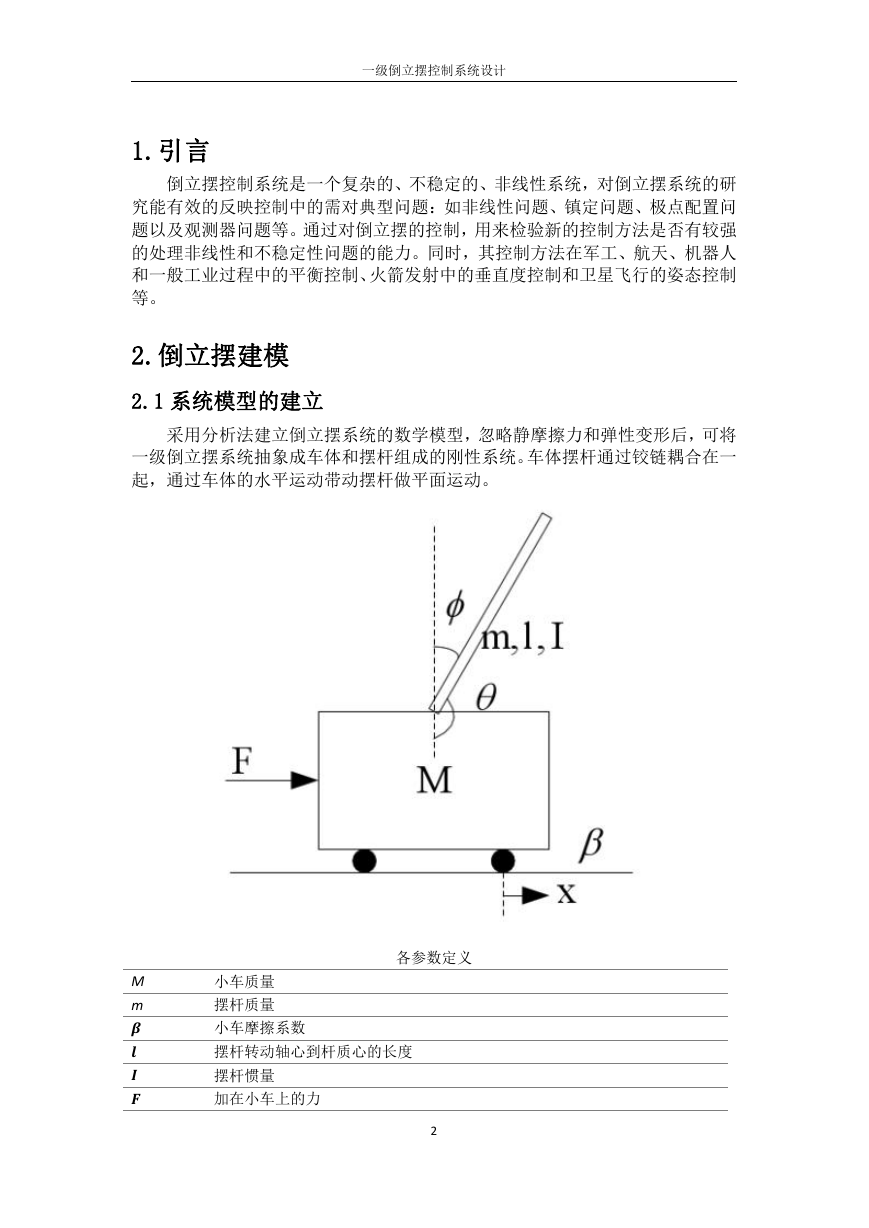
    一级倒立摆控制系统设计 1.引言 倒立摆控制系统是一个复杂的、不稳定的、非线性系统，对倒立摆系统的研 究能有效的反映控制中的需对典型问题：如非线性问题、镇定问题、极点配置问 题以及观测器问题等。通过对倒立摆的控制，用来检验新的控制方法是否有较强 的处理非线性和不稳定性问题的能力。同时，其控制方法在军工、航天、机器人 和一般工业过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行的姿态控制 等。 2.倒立摆建模 2.1 系统模型的建立 采用分析法建立倒立摆系统的数学模型，忽略静摩擦力和弹性变形后，可将 一级倒立摆系统抽象成车体和摆杆组成的刚性系统。车体摆杆通过铰链耦合在一 起，通过车体的水平运动带动摆杆做平面运动。 M m 各参数定义 小车质量 摆杆质量 小车摩擦系数 摆杆转动轴心到杆质心的长度 摆杆惯量 加在小车上的力 2
    一级倒立摆控制系统设计 小车位置 摆杆与垂直向上方向的夹角 摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下） X 摆杆受力分析： 竖直方向的方程为： 水平方向的方程为： （1）摆杆水平方向受力为11‘ （2）摆杆竖直方向受力为12‘ （3）摆杆与竖直方向夹角为1 （4）摆杆的中心位置坐标（1,1） 11‘ −12‘ =212 =22 +1 =+11 ' −12‘ +21=212 =22 1 =(−11)' =m+11−m11 =−11−11 +2+=− cosφ=−1,sinφ=0, 2=0 当摆杆与垂直向上方向之间的夹角相比，很小时，则进行以下处理： 将(2.1) 、(2.2)两个方程合并： (2.1) (2.2) (2.3) 3
    为了得到与现代控制理论下的表达式，即 u 为一般控制量，用 u 代表控制量 一级倒立摆控制系统设计 的输入力 F，将(2.3)线性化得到数学模型方程为： +2−= 同时系统整体受力为：++−= 将(2.4)、(2.5)求解得到： (2.4) (2.5) +2()2−()=()2 +()2+()−()2=() 将上式整理后得以 u 为输入量，以摆杆角为输出量的传递函数得： G   s  ( ) s  ( ) U s  4 s  (  2 ) I ml  p 3 s  2 ml s p ( M m mgl  ) p 2 s  bmgl p s 其中 p     M m I ml    2    ml 2   2.2 状态空间表达式得建立 设系统状态空间表达式：  X AX Bu y CX Du     对方程(2.4)、(2.5)求解得到： x  x   2 )  x  ( I ml            I M m Mml               I M m Mml ml       x   2 x   2 2 2 m gl     I M m Mml ( mgl M m )  I M m Mml       2   2 得到如下状态空间方程： 4 ( I ml      I M m Mml 2 ) ml   I M m Mml   u 2 u 2
    x      x               0 0 0 0           2 1 2 m gl    0 ml       I M m Mml  I M m Mml 一级倒立摆控制系统设计 2   I M m Mml ) 0 ( I ml      0 2 ( mgl M m  I M m M     ) m 2 l 2   2 0 0 1 0           x     x                       ( I M m Mml 2 2 0 I ml  )   0 ml ( ) I M m   Mml 2 u          x     x              0     0   u y  x         1   0    0   0   0   0   1   0     由： 且摆杆的转动惯量为 化简得： 以小车加速度作为输入的系统状态方程，设X=[x,,φ,]，u= ，则有： +2−= I  2 ml 1 3 =    3 g 4 l 3 4 l x  x      x                       0   1    0      0  0   0    0      0 0   0    0      1 0   0   3 g 4 l     0         x     x              u 0   1   0  3   4 l          y  x         1   0    0   0   0   0   1   0     x     x              0     0   u 2.2.1 倒立摆系统分析： 各参数具体数值 1.096Kg 0.109Kg 0 0.25m M m 5
    一级倒立摆控制系统设计 0.0034kg*m 加在小车上的力 小车位置 摆杆与垂直向上方向的夹角 X        0   1    0      0  0   0    0      0 0   0    0      1 0   0  29.4    0 得到状态空间表达式为： x x            x x                              x     x             1   0    0   0   0   0   1   0  x           y    0     1     0   3   u  0     0   u 2.3 系统能控性分析: 根据能控性判断方法：n=rank(BAB2B3B) 通过 matlab %**********************************************% % A=[0 1 0 0; 0 0 0 0;0 0 0 1;0 0 29.4 0;]; % B=[0;1;0;3]; % n=[B A*B A^2*B A^3*B]; % rank(n) 计算得 n=4 故系统能控 2.4 系统能观性分析： 根据能观性判断方法：n=rank(C,AC,2C,3C) %**********************************************% %判断能观性 %**********************************************% % A=[0 1 0 0; 0 0 0 0;0 0 0 1;0 0 29.4 0;]; % C=[1 0 0 0;0 0 1 0]; % m=[C ;C*A ;C*A^2 ;C*A^3]; % rank(m) 计算得 m=4 故系统能观 6
    一级倒立摆控制系统设计 得开环传递函数为： s 2.3 系统稳定性分析: 倒立摆以加速度为输入时 由   s G  ( ) s  ( ) U s  4 s  (  2 ) I ml  p 3 s  其特征根为： 2 ml s p ( M m mgl  ) p Gs = 2 s  bmgl p 3 2−29.4 2  1  5.1136 、 5.1136 此时具有一个在正半轴的极点，故开环系统不稳定。 simulink 仿真检验： 搭建如下模型： 得到如下输出仿真曲线： 7
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料