%"! RE=?8,D ES T=.,8 CEDG-/2.812 U81V/?;1-G 武 汉 工 业 学 院 学 报 ’""’ 年 文章编号：!""# $ %&&!（’""’）"% $ "!"% $ "( 拟合圆的几种方法 ! 徐国旺!，廖明潮’ （! ) 湖北工学院 基础科学部，湖北 武汉 %(""*&；’ ) 武汉工业学院 计算机与信息工程系，湖北 武汉 %(""’(） 摘 要：提出了几种拟合圆的方法，用这几种方法对一实例进行拟合，并用 +,-./0,-12, 显示用 这些方法拟合的效果。 关键词：拟合；+,-./0,-12,；加权平均；最小二乘法 中图分类号：3 ’# 文献标识码：4 平面内一些离散点从理论上构成一个圆，从这 些已知点坐标入手，求出该圆圆心位置坐标和圆的 半径大小，是某些领域中常会遇到的实际问题。如： 物理实验“用稳恒电流场模拟静电场”［!］中，把无限 长同轴圆柱体之间的等位线看作一个圆，实验测得 数据为等位点的坐标，要画出等位线就存在拟合圆 的问题。拟合圆的方法很多，下面探讨其中三种方 法。 ! 平均值法 对于均匀分布在圆上的 ! 个点（ "# ，$# ），% & !， ’，…，! ’ 从 理 论 上 讲，圆 心 坐 标 应 为（ ! ! # & ! "# ( !， ! $# ( !），圆心到圆上任一点的距离即为圆的半径。 ! # & ! 在实际问题中，实验测得的各点不可能正好均匀分 布在圆上，甚至有些点还不在圆上，但只要各离散点 分布较为均匀，仍可将（ $# ( ! ）作为圆 心坐标，圆心到各离散点的距离的平均值可作为圆 "# ( !， ! # & ! ! # & ! ! ! 半径的近似值。 下面以“用稳恒电流场模拟静电场”实验中一 组实测数据为例，运用上述方法拟合出圆，并将各数 据点和圆同时显示出来，以便直观地观察拟合效果。 实验测得一组等位点为｛& ’ ’，5 ’ 6｝，｛6 ’ %，6 ’ ’｝，｛* ’ "，& ’ "｝，｛% ’ (，& ’ !｝，｛( ’ "，6 ’ %｝，｛’ ’ !，* ’ !｝，｛’ ’ !，( ’ #｝，｛( ’ !，’ ’ %｝，｛% ’ 5，! ’ &｝，｛* ’ !，! ’ #｝，｛6 ’ (，’ ’ 6｝， ! 收稿日期：’""’ $ "’ $ ’* 作者简介：徐国旺（!#*6 $ ），男，湖北省潜江市人，讲师。 万方数据 ｛& ’ !，% ’ ’｝。以下过程用 +,-./0,-12, ［’］来完成。 78［!］： 9 - 9 :1;-［｛& ) ’，5 ) 6｝，｛6 ) %，6 ) ’｝，｛* ) "， & )"｝，｛% ) (，& ) !｝，｛( ) "，6 ) %｝，｛’ ) !，* ) !｝，｛’ ) !，( ) #｝，｛( ) !，’ ) %｝，｛% ) 5，! ) &｝，｛* ) !，! ) #｝，｛6 ) (，’ ) 6｝， ｛& ) !，% ) ’｝］； !’ 78［’］：9 , 9 ! 3=-［’］9 5 ) !&( (( 1 9 ! ［［1，!］］< !’ -［［1，!］］< !’ 8 1 9 ! 78［(］：9 > 9 ! 3=-［(］9 % ) #5 78［%］：9 ? 9 （, $ -［［1，!］］）’ @（> $ -［［1，’］］）’ ! " 3=-［%］9 ( ) !#! #% 78［ 5 ］：9 A?B- 9 :1;-CDE-［ -，F1;BD,GH=82-1E8 # < !’ 7I/8-1-G］； 78［*］：9 A?21? 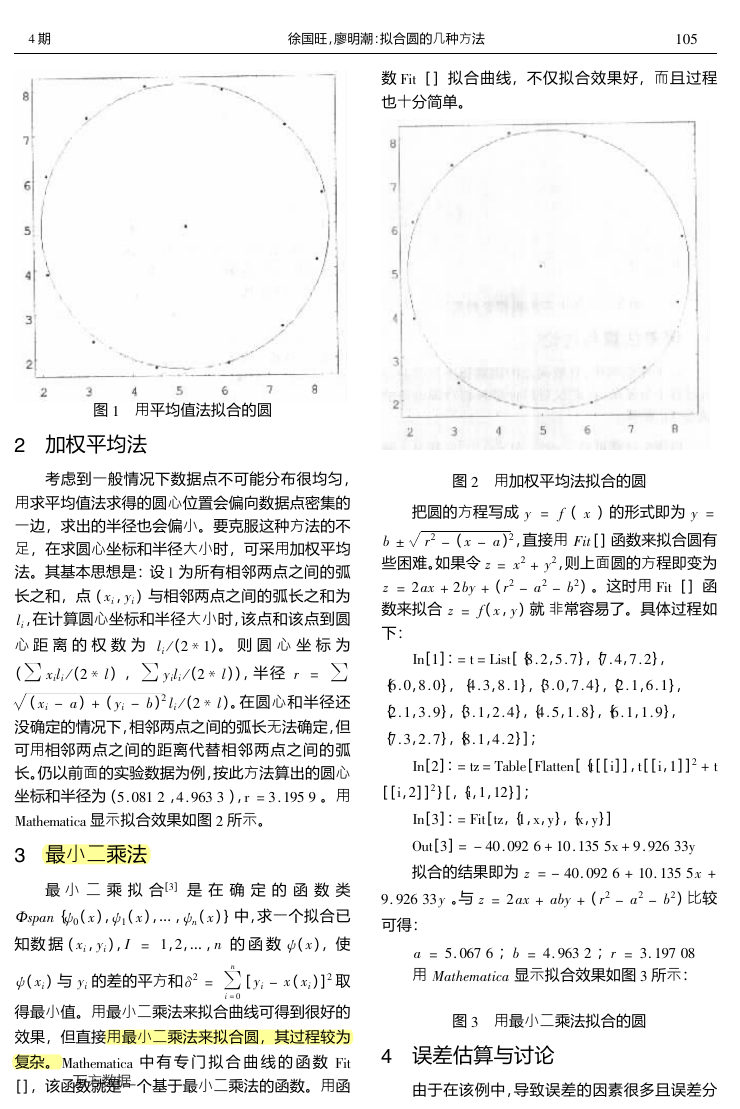9 J?,B.12;［K1?2D/［｛5 ) !&(( ， % ) #5""｝，( ) !#(#］］ 3=-［*］9 ) J?,B.12; ) 78［6］：9 L.EM［A?B-，A?21?，J?,B.12;［CE18- ［｛5 ) !&(( ，% ) #5&(｝］］，4;B/2-N,-1E#!，H?,0/#O?=/， F1;BD,GH=82-1E8# P F1;BD,GH=82-1E8 ，4Q/;#H,D;/］ 3=-［6］9 ) J?,B.12; ) 所得拟合效果如图 ! 所示。 

( 期 徐国旺，廖明潮：拟合圆的几种方法 $&! 数 640［］拟合曲线，不仅拟合效果好，而且过程 也十分简单。 图 ! 用平均值法拟合的圆 ! 加权平均法 考虑到一般情况下数据点不可能分布很均匀， 用求平均值法求得的圆心位置会偏向数据点密集的 一边，求出的半径也会偏小。要克服这种方法的不 ，#" 足，在求圆心坐标和半径大小时，可采用加权平均 法。其基本思想是：设 " 为所有相邻两点之间的弧 长之和，点（ !" ）与相邻两点之间的弧长之和为 ，在计算圆心坐标和半径大小时，该点和该点到圆 $" 心 距 离 的 权 数 为 $" %（#!!）。 则 圆 心 坐 标 为 （ " #"$" %（#! $）），半 径 & ’ " " !"$" %（#! $）， （ !" ( )） # $" %（#! $）。在圆心和半径还 （ #" ( +） # * 没确定的情况下，相邻两点之间的弧长无法确定，但 可用相邻两点之间的距离代替相邻两点之间的弧 长。仍以前面的实验数据为例，按此方法算出的圆心 坐标和半径为（$ % &’! # ，( % )*+ + ），, - + % !)$ ) 。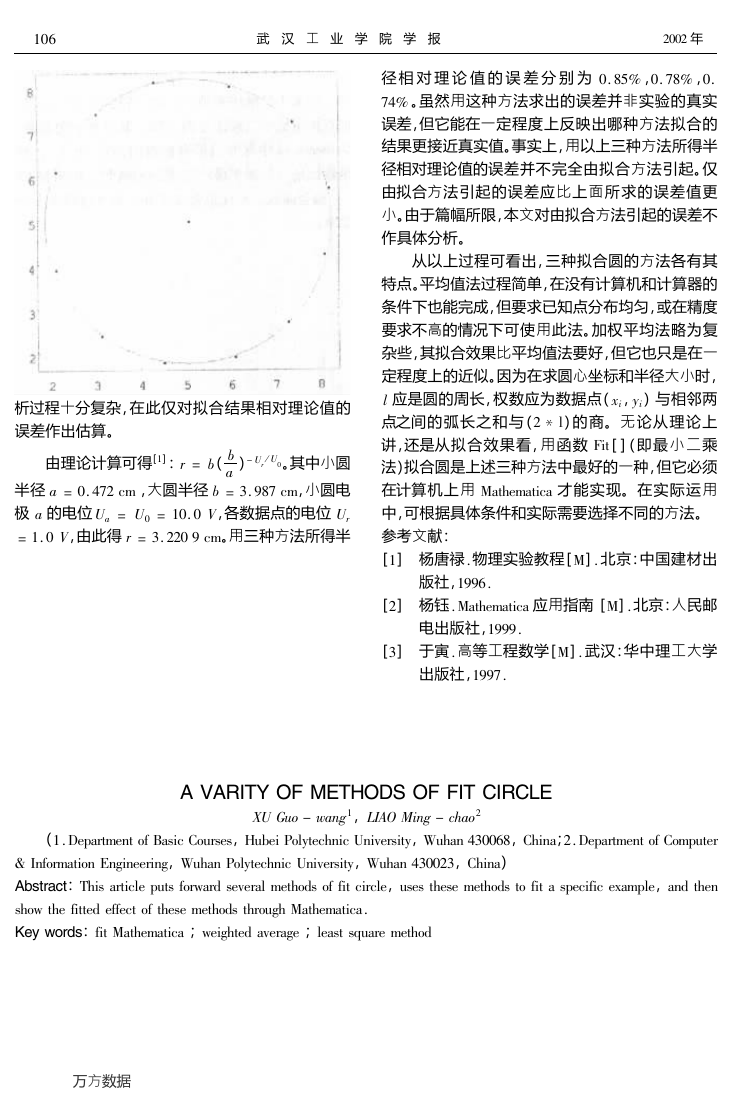用 ./0123/045/ 显示拟合效果如图 # 所示。 " 最小二乘法 （ !），…， ". !,-).｛ "& 知数 据（ !" （ !）， "! ），/ ’ !，#，…，. 的 函 数 最 小 二 乘 拟 合［+］ 是 在 确 定 的 函 数 类 （ !）｝中，求一个拟合已 （ !），使 " ［ #" ( !（ !" （ !" " 得最小值。用最小二乘法来拟合曲线可得到很好的 的差的平方和 . ## ’ " " ’ & ，#" ）与 #" ）］# 取 效果，但直接用最小二乘法来拟合圆，其过程较为 复杂。 ./0123/045/ 中 有 专 门 拟 合 曲 线 的 函 数 640 ［］，该函数就是一个基于最小二乘法的函数。用函 万方数据 图 # 用加权平均法拟合的圆 # &# ( （ ! ( )） 把圆的方程写成 # ’ 0（ ! ）的形式即为 # ’ #，直接用 2"3［］函数来拟合圆有 + 1 些困难。如果令 4 ’ !# * ##，则上面圆的方程即变为 （ &# ( )# ( +#）。这时用 640［］函 4 ’ # )! * # +# * 数来拟合 4 ’ 0（ !，#）就 非常容易了。具体过程如 下： 78［!］：- 0 - 94:0［｛’ % #，$ % ;｝，｛; % (，; % #｝， ｛* % &，’ % &｝，｛( % +，’ % !｝，｛+ % &，; % (｝，｛# % !，* % !｝， ｛# % !，+ % )｝，｛+ % !，# % (｝，｛( % $，! % ’｝，｛* % !，! % )｝， ｛; % +，# % ;｝，｛’ % !，( % #｝］； 78［#］：- 0< - =/>"2［6"/0028［｛0［［4］］，0［［4，!］］# ? 0 ［［4，#］］#｝［，｛4，!，!#｝］； 78［+］：- 640［0<，｛!，@，A｝，｛@，A｝］ BC0［+］- D (& % &)# * ? !& % !+$ $@ ? ) % )#* ++A 拟合的结果即为 4 ’ ( (& 5 &)# * * !& 5 !+$ $ ! * （ &# ( )# ( +#）比较 ) 5 )#* ++ # 。与 4 ’ # )! * )+# * 可得： ) ’ $ 5 &*; * ；+ ’ ( 5 )*+ # ；& ’ + 5 !); &’ 用 6)3789)3":) 显示拟合效果如图 + 所示： 图 + 用最小二乘法拟合的圆 # 误差估算与讨论 由于在该例中，导致误差的因素很多且误差分 

5"! 武 汉 工 业 学 院 学 报 %""% 年 径 相 对 理 论 值 的 误 差 分 别 为 " ( *+* ，" ( $** ，" ( $#* 。虽然用这种方法求出的误差并非实验的真实 误差，但它能在一定程度上反映出哪种方法拟合的 结果更接近真实值。事实上，用以上三种方法所得半 径相对理论值的误差并不完全由拟合方法引起。仅 由拟合方法引起的误差应比上面所求的误差值更 小。由于篇幅所限，本文对由拟合方法引起的误差不 作具体分析。 从以上过程可看出，三种拟合圆的方法各有其 特点。平均值法过程简单，在没有计算机和计算器的 条件下也能完成，但要求已知点分布均匀，或在精度 要求不高的情况下可使用此法。加权平均法略为复 杂些，其拟合效果比平均值法要好，但它也只是在一 ，.- 定程度上的近似。因为在求圆心坐标和半径大小时， + 应是圆的周长，权数应为数据点（ ,- ）与相邻两 点之间的弧长之和与（%! ,）的商。无论从理论上 讲，还是从拟合效果看，用函数 -./［］（即最小二乘 法）拟合圆是上述三种方法中最好的一种，但它必须 在计算机上用 01/23’1/.&1 才能实现。在实际运用 中，可根据具体条件和实际需要选择不同的方法。 参考文献： ［!］ 杨唐禄 4 物理实验教程［0］4 北京：中国建材出 版社，!))5 4 ［%］ 杨钰 4 01/23’1/.&1 应用指南［0］4 北京：人民邮 电出版社，!))) 4 ［(］ 于寅 4 高等工程数学［0］4 武汉：华中理工大学 出版社，!))$ 4 析过程十分复杂，在此仅对拟合结果相对理论值的 误差作出估算。 ）% & 由理论计算可得［!］：! " #（ # $ "。其中小圆 半径 $ " " ( #$% &’ ，大圆半径 # " ( ( )*$ &’，小圆电 极 $ 的电位 &$ " &" " !" ( " )，各数据点的电位 &! " ! ( " )，由此得 ! " ( ( %%" ) &’。用三种方法所得半 ’ & ! ! "!#$%& ’( )*%+’,- ’( ($% .$#./* /& 012 6 3$45!，6789 :-45 6 ;<$2% （! 4 73819/’3:/ ;< =1>.& ?;@9>3>，A@B3. C;,D/3&2:.& E:.F39>./D，G@21: #(""5*，?2.:1；% 4 73819/’3:/ ;< ?;’8@/39 H I:<;9’1/.;: J:K.:339.:K，G@21: C;,D/3&2:.& E:.F39>./D，G@21: #(""%(，?2.:1） !0123452：L2.> 19/.&,3 8@/> <;9M19N >3F391, ’3/2;N> ;< <./ &.9&,3，@>3> /23>3 ’3/2;N> /; <./ 1 >83&.<.& 3O1’8,3，1:N /23: >2;M /23 <.//3N 3<<3&/ ;< /23>3 ’3/2;N> /29;@K2 01/23’1/.&1 4 678 9:3;1：<./ 01/23’1/.&1 ；M3.K2/3N 1F391K3 ；,31>/ >P@193 ’3/2;N 万方数据 

拟合圆的几种方法 作者： 徐国旺， 廖明潮 作者单位： 徐国旺(湖北工学院,基础科学部,湖北,武汉,430068)， 廖明潮(武汉工业学院,计算机与信息 刊名： 英文刊名： 年，卷(期)： 工程系,湖北,武汉,430023) 武汉工业学院学报 JOURNAL OF WUHAN POLYTECHNIC UNIVERSITY 2002(4) 11次 被引用次数： 参考文献(3条) 1.杨唐禄 物理实验教程 1996 2.杨钰 Mathematica应用指南 1999 3.于寅 高等工程数学 1997 本文读者也读过(9条) 1. 张福民.曲兴华.吴宏岩.叶声华.ZHANG Fu-min.QU Xing-hua.WU Hong-yan.YE Sheng-hua 提高大型圆截面形状测 量精度的方法[期刊论文]-纳米技术与精密工程2009,7(4) 2. 刘志刚.鲍加贞.汤时虎.Liu Zhi-gang.Bao Jia-zhen.Tang Shi-hu 基于VC的最小二乘拟合圆在LAMOST中的应用 [期刊论文]-现代制造工程2008(1) 3. 李雄军.LI Xiong-jun 圆参数估计的相对代数距离法[期刊论文]-深圳大学学报（理工版）2006,23(2) 4. 戴丽.顾建刚 最小二乘圆法及其在原木定心中的应用[期刊论文]-木材加工机械2002,13(2) 5. 高鹏.杨军良.尚付鹏.Gao Peng.Yang Junliang.Shang Fupeng 凸轮轴测量中统一基准的方法[期刊论文]-计量技 术2009(7) 6. 朱方园.朱兴龙.周骥平.ZHU Fang-yuan.ZHU Xing-long.ZHOU Ji-ping 最小二乘圆法拟合激光斑点的一种方法 [期刊论文]-机械制造与自动化2006,35(4) 7. 李全信 圆曲线的拟合方法与精度分析[期刊论文]-北京测绘2001(3) 8. 樊俊屹.童小华.FAN Jun-yi.TONG Xiao-hua 基于不同拟合方法的圆曲线综合不确定性模型[期刊论文]-测绘与空 间地理信息2011,34(1) 9. 刘珂.周富强.张广军.LIU Ke.ZHOU Fu-qiang.ZHANG Guang-jun 半径约束最小二乘圆拟合方法及其误差分析[期 刊论文]-光电子·激光2006,17(5) 引证文献(11条) 1.赵瑾 喷管装配自动对准系统研究[期刊论文]-中北大学学报 2008(3) 2.王玉增.盖旭升.高常青.冯志全 轮辋逆向工程中设计参数的拟合算法[期刊论文]-机械强度 2008(2) 3.翟嘉.胡企千.吴金虎 地平式望远镜高度轴回转精度检测与计算方法[期刊论文]-机械制造 2008(3) 4.赵炯.侯晓梦.杨天琳.王军辉 基于图像传感器的圆心定位技术实用化研究[期刊论文]-传感器与微系统 2011(10) 5.李雄军 圆参数估计的相对代数距离法[期刊论文]-深圳大学学报（理工版） 2006(2) 6.佟林.王金涛.刘子勇.郭立功.暴雪松.张珑 基于光电内测法的立式罐容量计量中圈板半径拟合算法的研究[期刊论 文]-计量学报 2011(6) 7.王秀梅.曹秋霞 最小二乘圆法评定圆度误差的优化算法[期刊论文]-工具技术 2008(7) 8.李雄军 圆参数估计的相对代数距离法[期刊论文]-深圳大学学报（理工版） 2006(2) 9.郭磊民 银行验印系统中的印鉴自动识别[学位论文]硕士 2005 10.严子深 基于误差流理论（SOV）的机械加工误差诊断系统研究[学位论文]硕士 2005 11.陈基伟 工业测量数据拟合研究[学位论文]博士 2005 

本文链接：http://d.g.wanfangdata.com.cn/Periodical_whgyxyxb200204034.aspx