2014年山东济南稼轩中学小升初数学真题及答案.doc

发布时间：2022-09-02 发布人：admin 分类：说明书资料大小：0.25M 资料格式：doc 举报版权申诉

第1页 / 共6页

第2页 / 共6页

第3页 / 共6页

第4页 / 共6页

第5页 / 共6页

第6页 / 共6页

2014年山东济南稼轩中学小升初数学真题及答案

参考答案

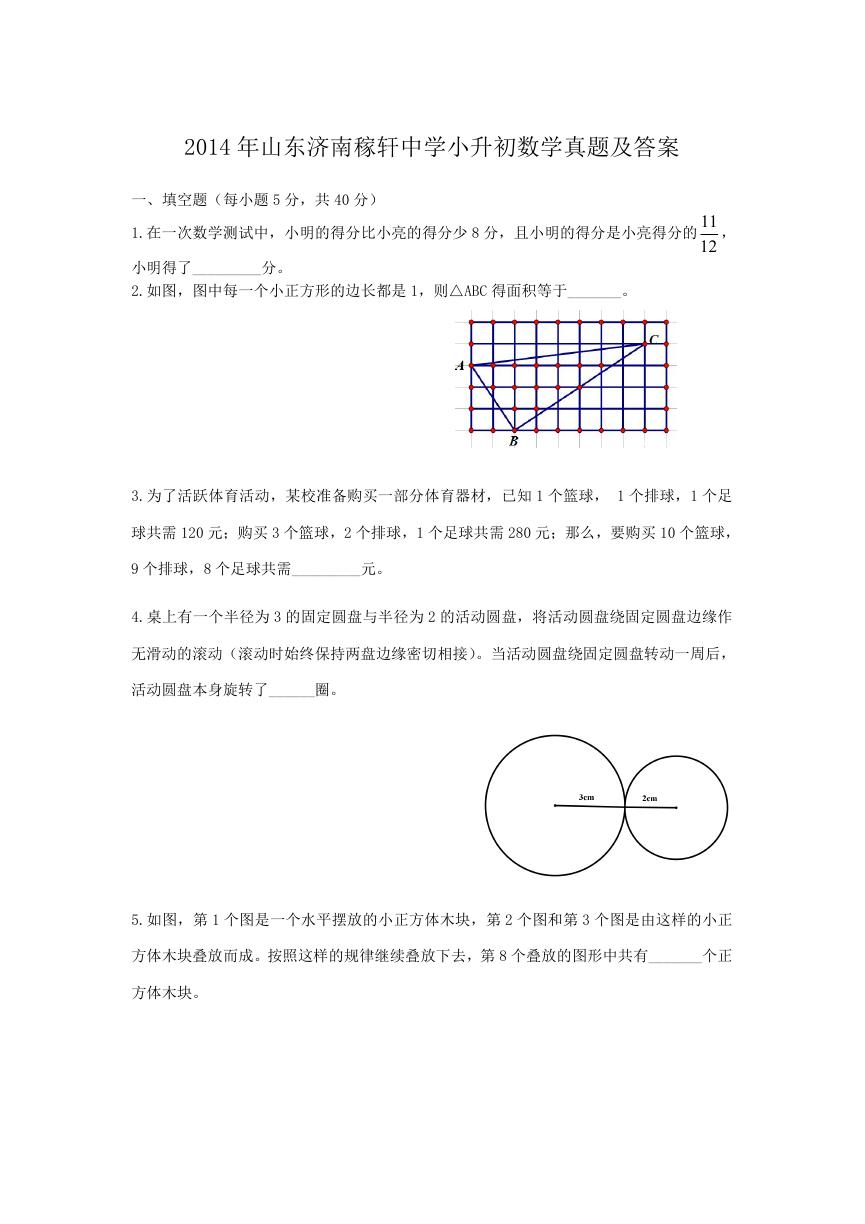
2014 年山东济南稼轩中学小升初数学真题及答案一、填空题（每小题 5 分，共 40 分） 1.在一次数学测试中，小明的得分比小亮的得分少 8 分，且小明的得分是小亮得分的小明得了_________分。 2.如图，图中每一个小正方形的边长都是 1，则△ABC 得面积等于_______。 11 12 ， 3.为了活跃体育活动，某校准备购买一部分体育器材，已知 1 个篮球， 1 个排球，1 个足球共需 120 元；购买 3 个篮球，2 个排球，1 个足球共需 280 元；那么，要购买 10 个篮球， 9 个排球，8 个足球共需_________元。 4.桌上有一个半径为 3 的固定圆盘与半径为 2 的活动圆盘，将活动圆盘绕固定圆盘边缘作无滑动的滚动（滚动时始终保持两盘边缘密切相接）。当活动圆盘绕固定圆盘转动一周后，活动圆盘本身旋转了______圈。 5.如图，第 1 个图是一个水平摆放的小正方体木块，第 2 个图和第 3 个图是由这样的小正方体木块叠放而成。按照这样的规律继续叠放下去，第 8 个叠放的图形中共有_______个正方体木块。

6.如下图是正方体的展开图，在顶点处标有 1~11 个自然数。当折叠正方体时，与数字 2 重合的数字为_________。 7.如图，甲、乙两动点分别从正方形 ABCD 的顶点 A、C 同时沿正方形的边开始移动，甲点顺时针方向环行，乙点逆时针方向环行，若乙的速度是甲的速度的 4 倍，则它们第 2014 次相遇在边____上。 8. 定义新运算 “  ”， 1= a  a ， a n  =2[ a  ( n  1)]  ( a n  ，已知 6=30 m  1) , 则 _______。 8=m  二、选择题（每小题 5 分，共 10 分） 9.观察下列等式 3 3 ， 3 3 9   ， 3 3 3 27    ， 3 3 3 3 81     ， 3 3 3 3 3 243      …… 则的末位数字是（）。 A.3 B．9 C．7 D．1 10. 商品甲的定价打九折后和商品乙的定价相等，下面说法中不正确的是（）。

A．乙的定价是甲的 90% B．甲比乙的定价多 10% C．乙的定价比甲少 10% D．甲的定价是乙的 10 9 倍   11   2 三. 计算题（本小题 10 分） 11.观察下列各式：， 1 2 3  1 3 4  1 5 7  1 1 2  （1） 1 1 2  （2） 1 1 3  1 2 3  1 3 5   ……        …… 2013 2014 1 2 1 3 1 3 4    1 3 1 4 ……根据以上规律计算： 1  1  2013 2015 四. 应用题（每小题 10 分，共 40 分） 12. 在一个底面积是 16 平方厘米的正方体铸铁中，以相对的两个面为底，挖出一个最大的圆柱体，求剩下的铸铁的表面积是多少平方厘米？（π取 3.14） 13.一个三位数，各个数位的数字之和为 18，其中个位上的数字比十位上的数字大 2，若把百位数字与个位数字对调，则得到的新三位数比原三位数大 99，求原三位数？ 14.某工厂加工一批零件，甲、乙、丙三人合作加工需要 15 天完成，由于机械故障，丙停止加工一天，乙就要多做三天，或者由甲、乙合作 1 天，问加工这批零件由甲单独完成需要多少天？ 15.一辆客车与一辆轿车都从 A 地驶往 B 地，其中客车的速度是轿车速度的 4 5 ，已知客车比轿车早出发 20 分钟，但在两地中点停了 5 分钟，才继续驶往 B 地；而轿车出发后中途没有停，直接驶往 B 地，最后轿车比客车早 5 分钟到 B 地。又知客车是上午 9 时从 A 地出发的，请问轿车是在上午什么时候追上客车的？

参考答案一、填空题 1.88 解析：小刚：8÷（1 ）=96 分小明：96-8=88 分 2.13 解析：根据毕克定律，内部点有 12 个，边界点有 4 个，所以面积等于： 12+4÷2-1=13 3.1120 解析：设篮球每个 x 元，足球每个 y 元，排球每个 z 元，则： x+y+z=120 3x+2y+z=280 两式相减的 2x+y=160 则 10x+9y+8z=8（x+y+z）+2x+y=8 120+160=1120 4.2.5 解析：（3+2）÷2=2.5 5.120 解析：第一图：1 个第二图：1+5=6 个第三图：1+5+9=15 个 ……….. 等差数列求和：第八图：1+5+9+13+……+29=120 6.5、7 7.BC 解析：设 AD=5，甲的速度为 1，则乙的速度为 4，第一次相遇：甲走的路程：（5+5）÷（4+1） 1=2 在 AD 边相遇第二次相遇：甲、乙合走 1 圈，甲走的路程：（5 4）÷（4+1） 1=4 在 CD 边相遇第三次相遇：甲走的路程：（5 4）÷（4+1） 1=4 在 C 点相遇第四次相遇：甲走的路程为 4 在 BC 边相遇第五次相遇：甲走的路程为 4 在 AB 边相遇第六次相遇与第一次相遇点重合，即说明周期是 5 2014÷5=402…….4 所以第 2014 次相遇与第四次相遇地点相同，即相遇在 BC 边上。 8.30 解析：a*1=a a*2=2 [a*(2-1)]-a=2 (a*1)-a=2a-a=a

a*3=2 [a*2]-a=2a-a=a ………… 则 a*n=a 由 m*6=30 得：m=30 所以 m*8=m=30 二、选择题 1.B 解析：3n 个位呈 3、9、7、1 的周期形式，所以 2014÷4=503…….2，所以个位数字是 9。 2.B 三、计算题 1.（1）原式=1- - + -…….+ - =1- （2）原式= + +……+ （） = （ + ） = （） = 四、应用题 1.解：正方体底面积为 16cm2，所以边长为 4 cm 底面：圆面积：π 22=4πcm2 圆柱侧面积：2 =16πcm2 表面积=4 个正方形面积+上下两个面挖掉圆后面积+圆柱侧面积 =4 42+（42-4π） +16π =96+8π =121.12 cm2 答：剩余部分表面积为 121.12 平方厘米。 2.解：设这个三位数百位、十位、个位分别是 a、b、c。 c-b=2 则：a+b+c=18 且：100（c-a）+（a-c）=99，即 99（c-a）=99 所以 c-a=1 联立可解得：a=6 b=5 c=7 所以原来三位数是 657。 3.解：设总工程量为 1，甲、乙、丙分别代表他们各自一天的工作量。

则：甲+乙+丙= 丙=乙丙=甲+乙联立解得：甲= 所以，甲单独完成需要：1÷ 答：甲单独完成需要。 4.解：轿车行驶全程比客车少用 20-5+5=20 分钟 V 客：V 轿=4:5 所以：t 客：t 轿=5:4 时间 20÷（5-4） 4=80 分钟即轿车全程 80 分钟，客车全程 100 分钟。 SAB=5 80=400 轿车到 B 的时间为 9:20+0:80=10:40 此时，客车还要 4 5=20 份距离从 10:40 倒算追及时间：20÷（5-4）=20 分钟所以：10:40-0:20=10:20 答：轿车在上午 10:20 追上客车。

分享到：

赞收藏

资料库

2014年山东济南稼轩中学小升初数学真题及答案.doc

相关推荐

小升初

热门标签

最新资料