GMM（高斯混合模型）详细推导.pdf-资料库

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第1页.png

第1页 / 共7页

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第2页.png

第2页 / 共7页

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第3页.png

第3页 / 共7页

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第4页.png

第4页 / 共7页

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第5页.png

第5页 / 共7页

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第6页.png

第6页 / 共7页

88ec8084-72e6-436f-8925-e38491ed6cf8.pdf-第7页.png

第7页 / 共7页

GMM：高斯混合模型高斯混合模型（Gaussian mixture model，簡稱 GMM）是單一高斯機率密度函數的延伸，由於 GMM 能夠平滑地近似任意形狀的密度分佈，因此近年來常被用在語音與語者辨識，得到不錯的效果。 1. 高斯混合密度函數的參數估測法在 d 維空間中的分佈不是橢球狀，那麼就不適合以一如果我們的資料個單一的高斯密度函數來描述這些資料點的機率密度函數。此時的變通方案，就是採用數個高斯函數的加權平均（Weighted Average）來表示。若以三個高斯函數來表示，則可表示成：此機率密度函數的參數為列條件：，而且要滿足下以此種方式表示的機率密度函數，稱為「高斯混合密度函數」或是「高斯混合模型」（Gaussian Mixture Model），簡稱 GMM。為簡化討論，我們通常假設各個高斯密度函數的共變異矩陣可以表示為：此時單一的高斯密度函數可表示如下：在上述方程式中，我們暫時省略了下標，以簡化方程式。若將上式對各個參數進行微分，可以得到下列等式： 1 nxxX,1333222111,;,;,;xgxgxgxp321321321,,,,,,,321,,13213,2,1,1000000122jIjjj22/22exp2,;xxxgTddj22222,;21,;,;xxgxxxgxgTdxxxgxxeedxgTTxxddxxddTT32322/212/2,;22,;22

上述這兩個等式，會在我們後面推導微分公式時，反覆被用到。當共變異矩陣可以表示成一個常數和一個單位方陣的乘積時，前述的可以簡化成：此的參數為，參數個數為。欲求得最佳的值，我們可依循最佳可能性估測法（MLE）原則，求出下列的最大值：為簡化討論，我們引進另一個數學符號：稱為事後機率（Post Probability），若用條件機率常用的表示方式，可寫成：因此可以看成是下列事件的機率：在觀測到亂數向量的值是時，此向量是由第個高斯密度函數所產生的。欲求的最大值，我們可以直接對及微分： 2 xp233322222111,,,;,;xgxgxgxpxp232221321321,,,,,,,,dddd36111111233322222111111,;,;,;lnlnln)(iiiniininiixgxgxgxpxpJ2333222221112,;,;,;,;xgxgxgxgxjjjjxj2333222221112,;,;,;,;332211xgxgxgxgxppxppxppjxpjpxpjxpjpxpxjpxjpxjjjjxjxj)(Jjj21212333222221112,;,;,;,;)(jjiniijjjiniiiijjjxxxxgxgxgxgJj

令上兩式為零，即可得到： (1) (2) 此外，我們人必須求對的微分，但因仍必須滿足總和為 1 的條件，因此我們引進 Lagrange Multiplier ，並定義新的目標函數為：將上三式相加： (3) 3 jjjiTjiniijjjjiTjiniiiijjjdxxxdxxxgxgxgxgJj31312333222221112,;,;,;,;)(niijniiijjxxx11niijnijiTjiijjxxxxd1121)(Jjj3211JJnew32123332222211111,,,,,,lniiinixgxgxg0,,,,,,,,12333222221112niiiijjijnewxgxgxgxgJ3,2,1,011jxniijjniiniiniixxx133122111niiiixxx1321321nni113,2,1,11jxnijnij

因此經由計算方程式事實上代表了是：仍是的導式並令其為零，我們得到方程式個純量方程式，共含及，這三個個未知數，但須特別注意的 , 是一組的函數，因此方程式個未知數的非線性聯立方程式，很難用一般的方法去解，通常我們是以方 , 為基礎來進行疊代法，流程如下：含程式 1. 設定一個起始參數值。（我們可令，並使用 K-means 的方式來計算群聚的中心點，以作為、和的起始參數值。） 2. 使用來計算 3. 計算新的值：、及， 4. 計算新的值： 5. 計算新的值： 6. 令若小於某一個極小的容忍值，則停並跳回步驟 2。止。否則令上述疊代方法一定會讓 Maximum），但我們無法證明此局部最大值是否就是全域最大值（Global Maximum）。有關這些方程式的另一種推導方法，以及這些方程式能夠讓遞增的證明，詳見下節說明。逐步遞增，並收斂至一個局部最大值（Local 逐步 2. 求取 GMM 參數的另一種方法 4 )(J2,13d36d36xj232221321321,,,,,,,,2,13d362,13232221321321,,,,,,,,31321123ix1ix2ix3ni~1jniijniiijjxxx11~jniijjiTjiniijjxxxxd1~~121~jniijjxn11~232221221321~,~,~,~,~,~,~,~,~~~~)(J)(J

在本節中，我們使用另一種來導出求取 GMM 參數的疊代公式。此方法所得到的疊代公式與前一節的公式完全相同，但本節之方法可證明此疊代公式可以逐次提高的值。首先我們說明一個重要的不等式。由於對數函數（Concave Function），滿足下列不等式：是一個凹函數推廣上式可得「簡森不等式」（Jensen’s Inequality）：其中必須滿足。假設我們現有的參數是，我們希望找出新的值，使得。以為例，可以表示成：因此在前面的推導中，的計算是根據，而且因為，因此我們可套用簡森不等式而得到。換句話就會大於，但通常我們希望是越大越好，因，那麼說，只要此最直覺的方法是直接求得使 1。由於是的函數，我們可以把和不相關的部分併入常數項，如下：為最大的值，那麼就會跟著變大，見圖 5 )(Jxxfln2121ln1ln1lnxxxxniiiniiixx11lnlninii11ˆˆJJ3mJ2333222221111,,,,,,lniiinixgxgxgJ)(ˆ,lnˆ,lnˆ,lnˆ,ˆ,ˆ,lnˆ,ˆ,ˆˆ,ˆ,ˆˆ,ˆ,ˆ,,,lnˆ1323,333222,222121,1113323,332222,221121,11123332222211123,3322,2221,111QxDxgxxDxgxxDxgxxxDxgxxDxgxxDxgxgxgxgxgxgxgJJniiiiiiiiiiiiiiiiiiiniiiiiiiniijxˆ233322222111ˆ,ˆ,ˆˆ,ˆ,ˆˆ,ˆ,ˆˆiiixgxgxgD131jijxQJJˆ0QJˆJJQJQ

欲求最佳之值，需引入 Lagrange multiplier：分別對微分，可得將上三式相加，可得：因此因此我們最後的結果可整理如下： 6 nijjiTjijjjijnijjjTjjdjjjijnijjijjijniiiiiiicxxdxcxxxcxgxcxgxxgxxgxQ122311122/2311123111233332222221,1112lnln2exp21lnln,,lnln,,ln,,ln,lnniijnijiTjiijjniijniiijjxxxxdQxxxQjj11211100jnijjiTjijjjijnewxxdxQQ132123132112lnln1jniinewniinewniinewxQxQxQ133122111000321niniiiinxxx113213211niijjjxn13,2,1,1

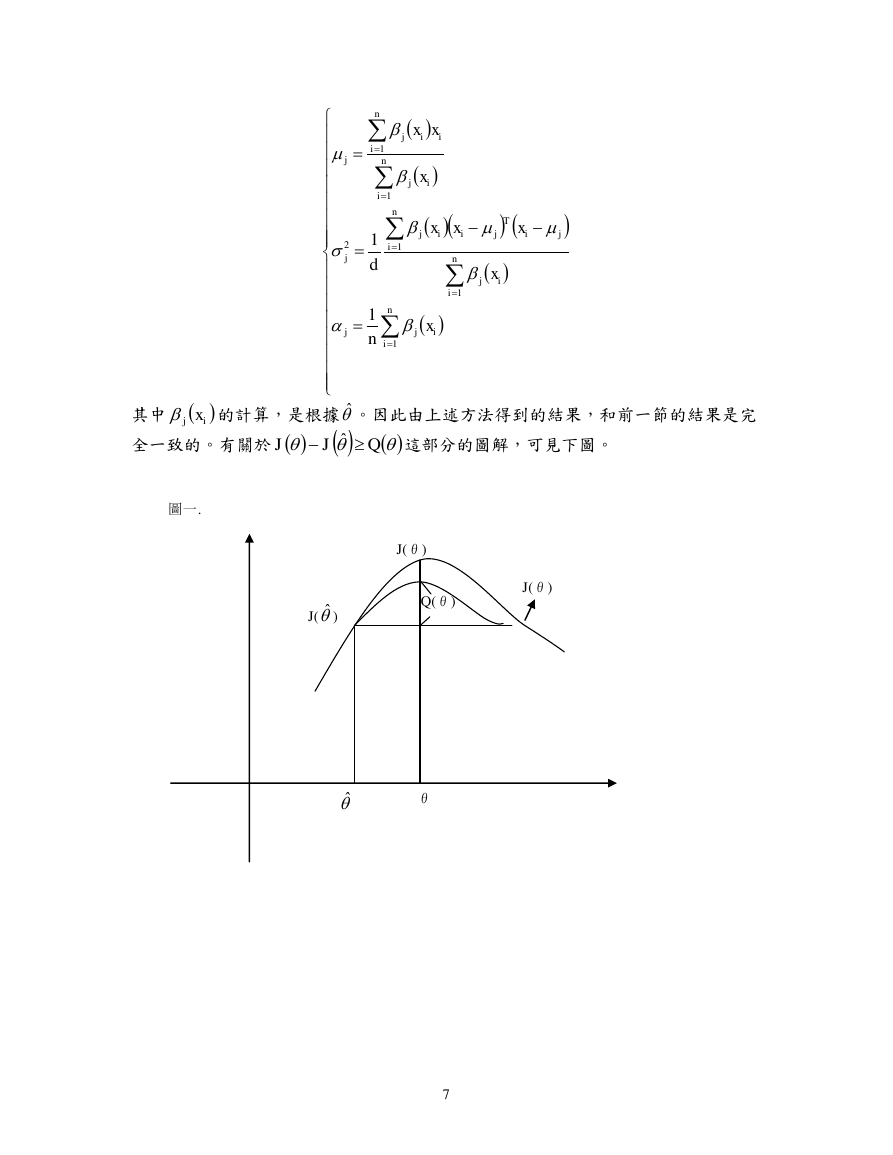
其中的計算，是根據。因此由上述方法得到的結果，和前一節的結果是完全一致的。有關於圖一. 這部分的圖解，可見下圖。 J(θ) Q(θ) J(θ) J( ) θ 7 inijjinijjiTjiinijjinijiinijjxnxxxxdxxx11121111ijxˆQJJˆˆˆ

资料库

GMM（高斯混合模型）详细推导.pdf

相关推荐

行业

热门标签

最新资料