ABAQUS-VUMAT初学者用户子程序小例子.pdf-资料库

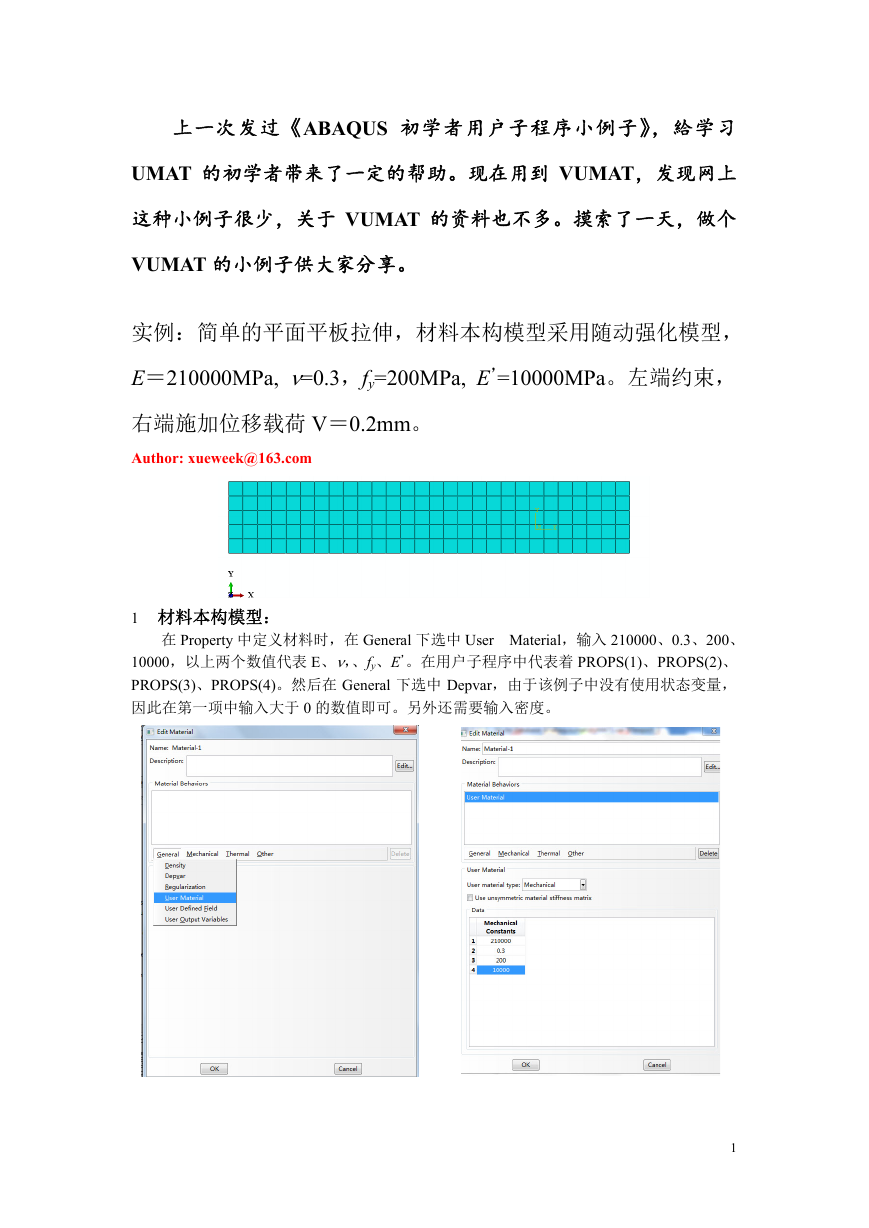
上一次发过《ABAQUS 初学者用户子程序小例子》，給学习 UMAT 的初学者带来了一定的帮助。现在用到 VUMAT，发现网上这种小例子很少，关于 VUMAT 的资料也不多。摸索了一天，做个 VUMAT 的小例子供大家分享。实例：简单的平面平板拉伸，材料本构模型采用随动强化模型， E＝210000MPa, ν=0.3，fy=200MPa, E’=10000MPa。左端约束，右端施加位移载荷 V＝0.2mm。 Author: xueweek@163.com 1 材料本构模型：在 Property 中定义材料时，在 General 下选中 User Material，输入 210000、0.3、200、 10000，以上两个数值代表 E、ν，、fy、E’。在用户子程序中代表着 PROPS(1)、PROPS(2)、 PROPS(3)、PROPS(4)。然后在 General 下选中 Depvar，由于该例子中没有使用状态变量，因此在第一项中输入大于 0 的数值即可。另外还需要输入密度。 1

建模大家都会，故省略 2 ABAQUS 中 STEP 的设置由于 VUMAT 需要用到 Explicit 求解，因此需要在 step 步骤中设置 explicit 选项，如下图，其设置可以用默认设置。 2

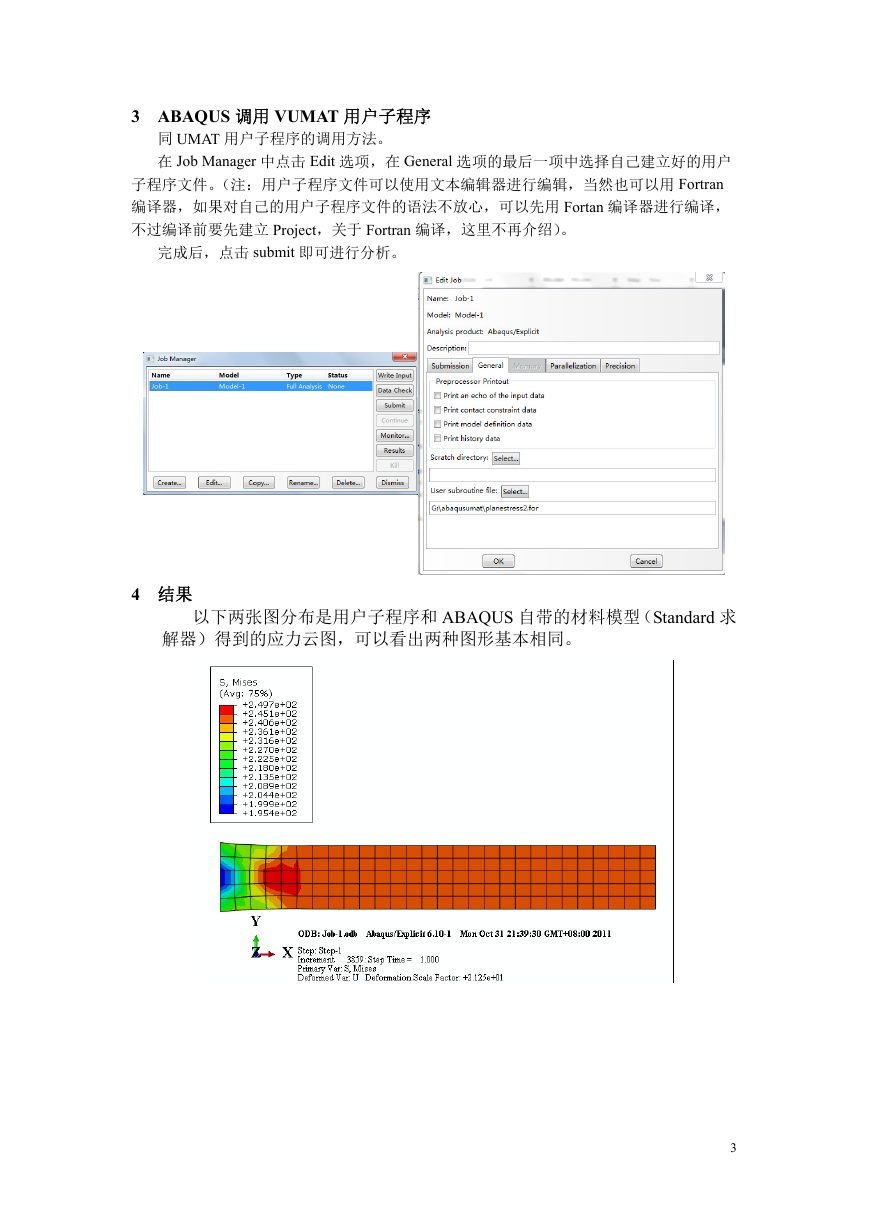
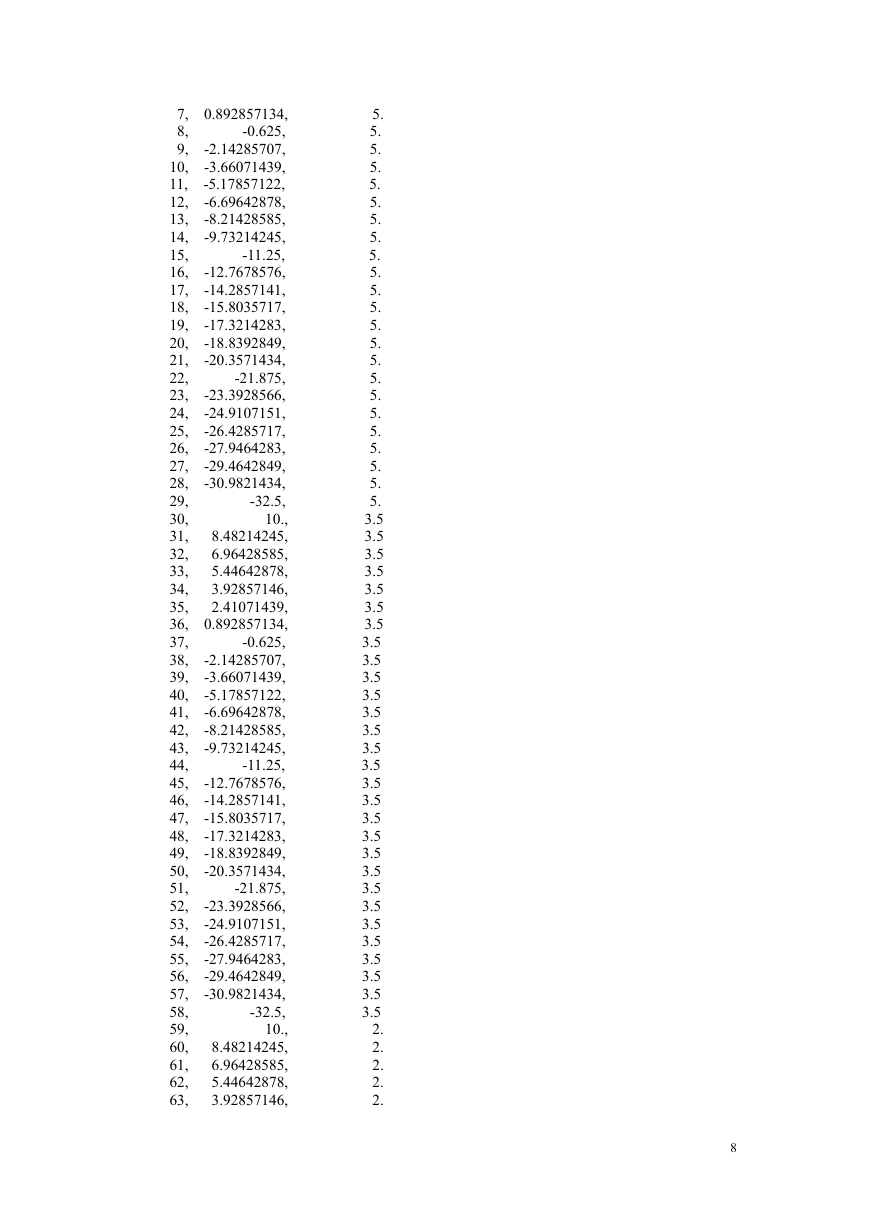
3 ABAQUS 调用 VUMAT 用户子程序同 UMAT 用户子程序的调用方法。在 Job Manager 中点击 Edit 选项，在 General 选项的最后一项中选择自己建立好的用户子程序文件。（注：用户子程序文件可以使用文本编辑器进行编辑，当然也可以用 Fortran 编译器，如果对自己的用户子程序文件的语法不放心，可以先用 Fortan 编译器进行编译，不过编译前要先建立 Project，关于 Fortran 编译，这里不再介绍）。完成后，点击 submit 即可进行分析。 4 结果以下两张图分布是用户子程序和 ABAQUS 自带的材料模型（Standard 求解器）得到的应力云图，可以看出两种图形基本相同。 3

5 VUMAT 子程序对于初学者来说，需要注意的是，FORTRAN 对于程序语言格式上的要求。例如，对于 FORTRAN 语言，前六个字符必须空出来，等等。检查语法最好的方法就是在 FORTRAN 编译器上进行编译。 SUBROUTINE VUMAT( C Read only - 1 nblock, ndir, nshr, nstatev, nfieldv, nprops, lanneal, 2 stepTime, totalTime, dt, cmname, coordMp, charLength, 3 props, density, strainInc, relSpinInc, 4 tempOld, stretchOld, defgradOld, fieldOld, 3 stressOld, stateOld, enerInternOld, enerInelasOld, 6 tempNew, stretchNew, defgradNew, fieldNew, C Write only - 5 stressNew, stateNew, enerInternNew, enerInelasNew ) C include 'vaba_param.inc' C C J2 Mises Plasticity with kinematic hardening for plane C strain case. C Elastic predictor, radial corrector algorithm. C C The state variables are stored as: C STATE(*,1) = back stress component 11 C STATE(*,2) = back stress component 22 C STATE(*,3) = back stress component 33 C STATE(*,4) = back stress component 12 4

C STATE(*,5) = equivalent plastic strain C C C All arrays dimensioned by (*) are not used in this algorithm dimension props(nprops), density(nblock), 1 coordMp(nblock,*), 2 charLength(*), strainInc(nblock,ndir+nshr), 3 relSpinInc(*), tempOld(*), 4 stretchOld(*), defgradOld(*), 5 fieldOld(*), stressOld(nblock,ndir+nshr), 6 stateOld(nblock,nstatev), enerInternOld(nblock), 7 enerInelasOld(nblock), tempNew(*), 8 stretchNew(*), defgradNew(*), fieldNew(*), 9 stressNew(nblock,ndir+nshr), stateNew(nblock,nstatev), 1 enerInternNew(nblock), enerInelasNew(nblock) C character*80 cmname C parameter( zero = 0., one = 1., two = 2., three = 3., 1 third = one/three, half = .5, twoThirds = two/three, 2 threeHalfs = 1.5 ) C e = props(1) xnu = props(2) yield = props(3) hard = props(4) C twomu = e / ( one + xnu ) thremu = threeHalfs * twomu sixmu = three * twomu alamda = twomu * ( e - twomu ) / ( sixmu - two * e ) term = one / ( twomu * ( one + hard/thremu ) ) con1 = sqrt( twoThirds ) C do 100 i = 1,nblock C C Trial stress trace = strainInc(i,1) + strainInc(i,2) + strainInc(i,3) sig1 = stressOld(i,1) + alamda*trace + twomu*strainInc(i,1) sig2 = stressOld(i,2) + alamda*trace + twomu*strainInc(i,2) sig3 = stressOld(i,3) + alamda*trace + twomu*strainInc(i,3) sig4 = stressOld(i,4) + twomu*strainInc(i,4) C C Trial stress measured from the back stress 5

s1 = sig1 - stateOld(i,1) s2 = sig2 - stateOld(i,2) s3 = sig3 - stateOld(i,3) s4 = sig4 - stateOld(i,4) C C Deviatoric part of trial stress measured from the back stress smean = third * ( s1 + s2 + s3 ) ds1 = s1 - smean ds2 = s2 - smean ds3 = s3 - smean C C Magnitude of the deviatoric trial stress difference dsmag = sqrt( ds1**2 + ds2**2 + ds3**2 + 2.*s4**2 ) C C Check for yield by determining the factor for plasticity, C zero for elastic, one for yield radius = con1 * yield facyld = zero if( dsmag - radius .ge. zero ) facyld = one C C Add a protective addition factor to prevent a divide by zero C when dsmag is zero. If dsmag is zero, we will not have exceeded C the yield stress and facyld will be zero. dsmag = dsmag + ( one - facyld ) C C Calculated increment in gamma (this explicitly includes the C time step) diff = dsmag - radius dgamma = facyld * term * diff C C Update equivalent plastic strain deqps = con1 * dgamma stateNew(i,5) = stateOld(i,5) + deqps C C Divide dgamma by dsmag so that the deviatoric stresses are C explicitly converted to tensors of unit magnitude in the C following calculations dgamma = dgamma / dsmag C C Update back stress factor = hard * dgamma * twoThirds stateNew(i,1) = stateOld(i,1) + factor * ds1 stateNew(i,2) = stateOld(i,2) + factor * ds2 stateNew(i,3) = stateOld(i,3) + factor * ds3 6

stateNew(i,4) = stateOld(i,4) + factor * s4 C C Update the stress factor = twomu * dgamma stressNew(i,1) = sig1 - factor * ds1 stressNew(i,2) = sig2 - factor * ds2 stressNew(i,3) = sig3 - factor * ds3 stressNew(i,4) = sig4 - factor * s4 C C Update the specific internal energy - stressPower = half * ( 1 ( stressOld(i,1)+stressNew(i,1) )*strainInc(i,1) 1 + ( stressOld(i,2)+stressNew(i,2) )*strainInc(i,2) 1 + ( stressOld(i,3)+stressNew(i,3) )*strainInc(i,3) 1 + two*( stressOld(i,4)+stressNew(i,4) )*strainInc(i,4) ) C C enerInternNew(i) = enerInternOld(i) C 1 + stressPower / density(i) C C Update the dissipated inelastic specific energy - plasticWorkInc = dgamma * half * ( 1 ( stressOld(i,1)+stressNew(i,1) )*ds1 1 + ( stressOld(i,2)+stressNew(i,2) )*ds2 1 + ( stressOld(i,3)+stressNew(i,3) )*ds3 1 + two*( stressOld(i,4)+stressNew(i,4) )*s4 ) C enerInelasNew(i) = enerInelasOld(i) C 1 + plasticWorkInc / density(i) 100 continue C return end 6 INP 输入文件 *Heading ** Job name: Job-1 Model name: Model-1 ** Generated by: Abaqus/CAE 6.10-1 *Preprint, echo=NO, model=NO, history=NO, contact=NO ** ** PARTS ** *Part, name=Part-1 *Node 1, 10., 5. 2, 8.48214245, 5. 3, 6.96428585, 5. 4, 5.44642878, 5. 5, 3.92857146, 5. 6, 2.41071439, 5. 7

7, 0.892857134, 5. 8, -0.625, 5. 9, -2.14285707, 5. 10, -3.66071439, 5. 11, -5.17857122, 5. 12, -6.69642878, 5. 13, -8.21428585, 5. 14, -9.73214245, 5. 15, -11.25, 5. 16, -12.7678576, 5. 17, -14.2857141, 5. 18, -15.8035717, 5. 19, -17.3214283, 5. 20, -18.8392849, 5. 21, -20.3571434, 5. 22, -21.875, 5. 23, -23.3928566, 5. 24, -24.9107151, 5. 25, -26.4285717, 5. 26, -27.9464283, 5. 27, -29.4642849, 5. 28, -30.9821434, 5. 29, -32.5, 5. 30, 10., 3.5 31, 8.48214245, 3.5 32, 6.96428585, 3.5 33, 5.44642878, 3.5 34, 3.92857146, 3.5 35, 2.41071439, 3.5 36, 0.892857134, 3.5 37, -0.625, 3.5 38, -2.14285707, 3.5 39, -3.66071439, 3.5 40, -5.17857122, 3.5 41, -6.69642878, 3.5 42, -8.21428585, 3.5 43, -9.73214245, 3.5 44, -11.25, 3.5 45, -12.7678576, 3.5 46, -14.2857141, 3.5 47, -15.8035717, 3.5 48, -17.3214283, 3.5 49, -18.8392849, 3.5 50, -20.3571434, 3.5 51, -21.875, 3.5 52, -23.3928566, 3.5 53, -24.9107151, 3.5 54, -26.4285717, 3.5 55, -27.9464283, 3.5 56, -29.4642849, 3.5 57, -30.9821434, 3.5 58, -32.5, 3.5 59, 10., 2. 60, 8.48214245, 2. 61, 6.96428585, 2. 62, 5.44642878, 2. 63, 3.92857146, 2. 8

资料库

ABAQUS-VUMAT初学者用户子程序小例子.pdf

相关推荐

开发技术

热门标签

最新资料