分布式电源并网的多目标规划与决策研究.pdf-资料库

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 分布式电源并网的多目标规划与决策研究熊兰，吴雄，杨子康，范禹邑，曾泽宇* （重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400030）摘要：针对 DG 选址定容问题，建立了综合网损、电压偏差和电压稳定性的多目标模型，并提出了一种改进多目标差分进化算法。在传统多目标差分进化算法中引入多目标排名变异算子增加优秀个体参与变异操作的概率，以加强算法的收敛速度以及搜索成功率；采用控制参数自适应调整策略，提高了算法的鲁棒性。首先通过改进多目标差分进化算法求取多目标选址定容模型，然后利用三角模糊法层次分析法和熵权法确定主、客观权重，通过博弈论求取主客观组合权重，最后根据灰色关联决策模型对各方案进行决策。以 IEEE-33 节点系统为算例验证了所提方法的有效性。关键词：分布式电源；选址定容；多目标进化算法；灰色关联决策中图分类号：TM7 Research on multi objective programming and decision making of distributed power grid XIONG Lan, WU Xiong, YANG Zi-kang, FAN Yuyi, ZENG Zeyu (State Key Laboratory of Power Transmission Equipment & System Security and New Technology(Chongqing University),Chongqing 400044) Abstract: The paper proposes a multi-objective decision-making approach for distributed generation(DG) locating and sizing，comprehensively considering three indices of network power losses，voltage deviation and static voltage stability. Moreover, it presents an improved differential evolution algorithm for multi-objective optimization. Ranking-based mutation operator is introduced to enhance the convergence speed and search success rate by increasing the probability of excellent individuals involved in mutation operations. The adaptive adjustment strategy for control parameters improves the robustness of the algoritResearch on multi objective programming and decision making of distributed power gridhm. Firstly, the improved multi-objective differential evolution algorithm is applied to obtain multi-objective location model, Secondly it uses the triangular fuzzy AHP and entropy method to determine the subjective and objective weight, through the game theory to obtain the combination weight. Finally, the grey incidence decision-making model is employed to finally obtain the best solution. The example of IEEE-33 system verifies the effectiveness of the proposed method.) Key words: distributed generation(DG); locating and sizing; multi-objective optimization evolutionary algorithm; grey relational decision 0 引言分布式电源（DG）因其占地少、投资少、见效快、调峰方便、灵活性高、清洁环保等优点，已成为新世纪电力产业的重要发展方向之一。分布式电源接入配电网会改变配电网的结构和运行，合理的安装位置和容量可有效改善配电网电压分布、减少系统有功网损、提高线路负载能力等[1,2]。但如果 DG 配置不合理，将得不到相应的效果，甚至可能威胁电网安全稳定的运行。为了更好地利用分布式能源，应先解决规划阶段分布式电源的配置问题，即选择合适的安装位置及容量。 DG 选址定容问题是综合考虑经济性，安全性和稳定性等多方面的多目标优化问题。二次规划法[3]、粒子群算法[4]等方法被应用于求解多目标选址定容问题，但它们在将多目标问作者简介：熊兰(1972—)，女，博士，教授主要从事脉冲功率技术的水处理应用、电气设备在线智能化监测技术方面的研究. E-mail: 2570050627@qq.com - 1 -

45 50 55 中国科技论文在线题通过权重相加处理成单目标问题存在权重选择合理性及子目标之间关系处理=不恰当的问题。近年来，多目标进化算法(MOEA)的不断发展，为解决多目标优化问题提供了新的途径。 MOEA 算法不需要提前设置权重，而是得到一组均匀分布的 pareto 最优解集。决策者可以根据需求，利用多属性决策方法从中选取一个或多个最优解。 http://www.paper.edu.cn 微分进化(differential evolution，DE)算法是一种基于新型进化算法，因其易使用、鲁棒性强和收敛性好，已被广泛应用到实际工程中[5,6]。为使其适用于多目标优化问题的求解，文献[7]将 NSGA-II 中 pareto 等级和拥挤距离排序操作引入 DE 算法中，提出了多目标差分进化算法(differential evolution of multiobjective optimization，DEMO)。然而，DEMO 算法中参与变异操作的个体完全来自于随机选择，存在选择压力小，收敛慢的不足，并且交叉、变异操作对参数依赖性强，其固定的参数设置不具备普适性。针对 DEMO 存在的问题，本文引入差分排名变异算子和控制参数自适应调整策略操作，并用其求解以降低配电网网损、提高配电网电压质量和电压稳定性为目标，的多目标优化配置模型。对求得的 pareto 最优解集，使用灰色关联决策模型对其进行决策从而得到最终方案。以 IEEE-33 节点系统为算例验证所提方法的有效性。 1 分布式电源选址定容的数学模型 60 1.1 目标函数 65 70 75 电力系统运行的基本要求是能够保证可靠的持续供电、具备良好的电能质量和运行的经济性。依据以上要求，本文以降低配电网网损、提高配电网电压质量和电压稳定性为目标，建立了多目标优化配置模型。 1）配电网网络损耗网损是衡量配电网运行经济性的一项重要指标,系统有功损耗的数学表达式可以表示为 P loss = B  = k 1 2 G V V j 2 [ k i + − θθ ( 2 VVcos − i j i j )] (1) 式中， B 是系统支路总数； kG 是连接节点 i 和 j 的支路 k 的电导； V 和 θ 分别是节点电压幅值和相位。 2）节点电压偏差 DG 能有效改善配电网中节点电压的分布情况，各节点与系统正常电压值偏差的均值可用来表征系统的电压偏差，其数学表达式为 Δ U = N ( 1 − 1 N −  1) = i 1 − | U U i iref (2) | 式中， UΔ 是节点电压偏移值;N 是配电系统的节点总数; iU 表示 DG 接入后节点 i 的电压幅值; irefU 表示配电系统节点 i 额定电压幅值，其值为 1.0 p.u 。 3）静态电压稳定性指标 DG 的接入对配电网电压稳定水平有很大的影响，合理地规划 DG 可以有效地改善电压稳定水平，保证系统更加稳定的运行。通常用静态电压稳定指[8]（ Voltage Stability Index, VSI）来表征系统电压稳定性。对于支路 k，有 VSI k = 4[( X P R Q ij j ij j − + 2 ) 2 ( X Q R P V ij j i ij j ) ] / ( ) 4 V i (3) + - 2 -

中国科技论文在线 http://www.paper.edu.cn 80 式中， ijR 和 ijX 分别是支路 k 的电阻和电抗； jP 和 jQ 分别是支路 k 的接收端点 j 的有功功率和无功功率。全系统的静态电压稳定指标 VSI 取所有支路中的最大静态电压稳定指标，即 (4) ,..., max{ VSI VSI = VSI VSI 2 , 1 }k 综述所述，在综合考虑配电网系统的经济性、安全性和稳定性后，分布式电源的多目标 85 函数为： 1.2 约束条件 1）功率平衡约束： min( , , ) f f f 1 3 2 = min( , P loss Δ ) U VSI , (5) +  ( P P  i    ( Q Q  + i − − − − N  = j 1 N  j = 1 DGi P V V G cos ( j ij Li i DGi Q V V G sin ( j ij Li i θ ij θ ij + + B sin ij ij B cos ij ij = ) 0 = ) 0 (6) 90 式中， iP 、 DGiP 、和 LiP 分别是在节点 i 处发电机有功出力、 DG 有功出力和有功负荷； iQ 、 DGiQ 和 LiQ 分别是在节点 i 处发电机无功出力、 DG 无功出力和无功负荷。 2）节点电压约束: i V min ≤ ≤ V V i i (7) max 式中， miniV 和 maxiV 分别是 i 节点电压幅值上下限。 95 3）安装点 DG 安装容量约束： P DGi P≤ DGi max (8) 式中， max DGiP 为 i 节点 DG 最大允许安装容量。 4)DG 接入总容量约束：  ∈ i DG 安装候选节点 ≤ P DGi P D G max (9) 100 式中： maxDGP 是配电网 DG 最大允许安装总容量。 5)DG 最大安装节点个数约束；  ∈ i DG 安装候选节点 ≤ m M (10) 式中，m 代表 DG 安装候选节点节点是否安装 DG，1 代表安装，0 代表未安装，M 是安装 DG 最大节点数。 105 2 改进多目标微分进化算法 1)多目标排名变异算子在自然界的进化法则中，优秀的个体往往拥有更多有价值的成分，因而有更大的可能性引导子代向更优秀的方向进化。在该规律的启发下,Gong 和 Cai 针对单目标优化问题设计了差分排名变异算子。该算子对整个 DE 种群按目标函数值从优到劣进行排序,优秀的个体以较大的选择概率参与变异,而低劣的个体以较小的选择概率参与变异。[9] 110 - 3 -

中国科技论文在线 http://www.paper.edu.cn 考虑到 DEMO 算法采用的是 DE/rand/l 变异算子，参与变异操作的个体完全来自于随机选择，存在选择压力小，收敛慢的不足，本文将差分排名变异算子引入到多目标差分进化算法中。然而，不同于单目标优化问题，多目标优化的个体间很多无法直接比较，因此将 NSGA-II 中 Pareto 非劣等级和拥挤距离排序操作引入到排名变异算子中对个体进行排名。个体排名规则为：1）优劣等级越低的个体越优秀；2）优劣等级相同时，拥挤距离越大的个体越优秀。对整个种群进行优劣排序后,分配每个个体的排名值，优劣顺序为第 i 的排名值为： 115 R NP − i= i+1，i=1,2,  (11) ,NP 由式 11 可知，越优秀的个体被赋予越大的排名值。排在第 i 位的个体的被选择的概率 120 为：，i=1,2, ,NP (12) iR +  i= p 2 + (1  ) NP + 式 12 表明，越优秀的个体被选中的概率越大。 2）控制参数自适应调整 DEMO 算法的变异因子 F 和交叉因子 CR 的取值对算法的收敛速度及稳定性有很大影响。F 取值较大时,可增大变异个体与当前个体的差异,有利于保持种群的多样性和全局收敛;F 取值较小时,对当前个体的变异不大，能起到局部精细化搜索的作用,有利于局部搜索。CR 越大，变异矢量对试验矢量的贡献越多，对目标个体矢量的破坏也越大，不利于优秀个体保留到下一代，但有利于淘汰掉劣势个体；反之，CR 越小，越不易生成新个体，有利于保留优秀个体，但会使搜索缓慢。因此，理想的情况是，F 和 CR 的值随着个体的优劣度的变化而自适应改变。对于较优秀的个体，取较小的 F 和 CR，增大其保留到下一代的机会；对于较劣势的个体，取较大的 F 和 CR，加快其结构的改变，以生成更优的个体。基于以上分析，本文提出了变异因子 F 和交叉因子 CR 自适应取值策略： 125 130 = F F i min + ( F max − − NP R ) i  − min 1 NP F (13) = CR CR i min + ( CR max − CR − NP R ) i  − min 1 NP (14) 135 式中， iR 为个体排名值，NP 为种群个数， maxF 和 minF 分别为 F 上下限， maxCR 和 minCR 分别为 CR 的上下限。 3 多属性决策方法 140 通过基于改进多目标差分进化算法可以得到当前时步的 pareto 最优解集，作为 DG 安装的可行方案。由于 pareto 最优解集包含多个 DG 安装方案，故需要结合实际情况和决策者偏好进行多属性决策。本文针对有功网损、节点电压偏差和静态电压稳定性 3 个属性，首先根据熵权法确定各属性的客观权重，然后利用三角模糊法层次分析法确定主观权重，通过博弈论求取主客观组合权重，最后根据灰色关联决策模型对各方案进行决策。 3.1 基于灰色关联分析法的多属性决策灰色关联分析法对样本量的多少和样本有无规律无特别要求，而且计算量小，实现方便， 145 更不会出现量化结果与定性结果不符的情况[10]。 - 4 -

中国科技论文在线 http://www.paper.edu.cn 灰色关联分析综合评价[11]的基本步骤如下：（1）确定比较序列和参考序列：有 m 个待评估方案，每个方案有 n 项指标， ijx 代表第 i 个方案的第 j 个指标值，则 m 个方案的全部指标构成评估矩阵 X = ( )ij m n x × 。为消除各变量的量纲效应，采用标准 0-1 变换对待评估矩阵进行标准化处理。设第 i 个评估点的第 j 个指标值规范化后为 ijr , max,jx 和 min,jx 分别为所有样本中第 j 个指标的最大和最小值。当指标为正指标时，即指标值越大越好，指标的标准化公式为： 150 = r ij x ij x max, j − x − j min, x min, j (15) 当指标为逆指标时，即指标值越小越好，指标的标准化公式为： 155 = r ij 待评估矩阵 x 经标准化处理后得到矩阵 R x = (16) ，即比较序列。本文取其矩阵 R − − x max, j x ij max, j x min, j r × ( )ij m n = r 中每个指标的最优值 * i （2）计算关联系数 r= max, i 组成理想方案 * R r r ( *2 , *1 ,  r , * )i ，即为参考序列。关联系数 ij ε 是待评估方案序列曲线 i 与理想方案序列曲线在指标 j 的相对差值，其计 160 算公式为 ε ij = − min min ∈ i m j n r r * i ij + − ∈ r r * i ij + ρ ρ max max ∈ i m j n ∈ − r r * i ij − max max ∈ i m j n ∈ r r * i ij (17) 式中： ρ为分辨系数， ρ∈[0，1] ，由式()计算可得到各方案与理想方案在全部指标上的关联系数矩阵 = ε ε × )ij m n ( 。（3）计算灰色关联度：第 i 个评价方案与理想方案的关联度为： 165 γ i 式中， j ω 为第 j 个指标的权重。 3.2 基于博弈论的组合赋权法 n =  = j 1 ωε j ij (18) 采用基于组合权重的灰色关联分析法评估 DG 安装备选方案的关键在于指标的权重的选取，其取值直接关乎到评估结果的科学合理性。客观权重体现了属性的信息量，主观权重体现了属性的价值量，主客观权重的组合实现了信息量和价值量的统一。本文采用基于博弈论的组合赋权法来确定各指标的权重。 3.2.1 主观权重求取在进行主观赋权时，考虑到决策者评判信息具有模糊性和不确定性，采用三角数模糊层次分析法[12]来确定评估体系各个指标的主观权重。为了避免单一专家的评判可能会由于个人的知识层面,习惯等存在一定的偏差，采用多个专家的综合评判意见,取其平均值作为三角 170 175 - 5 -

中国科技论文在线模糊数。其具体应用步骤如下。 http://www.paper.edu.cn 1）构造模糊判断矩阵，由专家对评价指标两两进行比较，并用三角模糊数构造模糊判断矩阵，记为 = a ij ( l m u ij ij ij , , ),且 a j i = a − ij 1 (19) 180 式中： ija 表示表示模糊判断矩阵中第 i 个评价指标相对第 j 个评价指标的重要程度值；本文采用五个标度[13]如表 1 所示。优先度 ija ija 表 1 比较刻度表取值 (1,1,1) (1,1.5,2) (1.25,1.5,2) (1.25,1.5,2.5) (1.5,2,2.5) 上述值取倒数代表含义 i 和 j 同等重要 i 比 j 稍微重要 i 比 j 比较重要 i 比 j 重要得多 i 比 j 极其重要 j 比 i 的优先度 n 位专家利用模糊数来表达他们对各指标的偏好通过对同一层次的各个要素进行两两 185 190 比较得到一组模糊数，经过 n 位专家评判后得到平均三角模糊数为分别为 + + + + + + = l l ( 1 2 M l n m m 2 1 ,  + n m u u 2 n 1 , u n ) (20)  + n  + n 2）对于模糊判断矩阵，计算各个指标综合重要程度值： = S i m ⊗ a ij = i 1 n m   [ = i i = 1 1 a − ] ij 1 (21) 其中， iS 表示模糊判断矩阵中第 i 个评价指标相对其他所有指标的综合重要程度值。 3）计算 iS 重要于 jS 的可能性程度： ( ≥ V S S j  1  −  l u i i  − ( ) ( ) m u m l  i i  4）计算出个指标权重： − = − 0 ) i i i ≥ i m m j ≤ ≥ m m u l j i , j i 其他 (22) = MinV S S j ( ( )) ≥ i 其中 D Ai , W = D D ( A 2 , A 1 ,  D , An ) (23) 然后再将其归一化，即得到权重向量。 3.2.2 客观权重求取 195 本文采用熵权法[14]求取各指标客观权重，对归一化后的决策矩阵 R，依据标准化决策矩阵，可求得第 i 个评价样本第 j 个指标的特征比重， = p ij r ij m  = i 1 r ij - 6 - (24)

中国科技论文在线第 j 个指标的熵值为： = − e j 1 ln 200 当 ijp =0 时，取 ln ijp =0, 则第 j 个指标的熵权为 ω j = http://www.paper.edu.cn p ij ln p ij (25) m  m = i 1 − 1 e j − (1 m = j 1 e j (26) ) 3.2.3 基于博弈论的组合赋权法基于博弈论[15]的权重集化模型的思想是在不同权重之间寻找一致或妥协，极小化可能 205 的权重与各基本权重之间的偏差获取最优权重。用 L 种方法对指标分别赋权，得到权重集由 L 种权重向量组成的权重向量集为合为： = ω ω ω , W ω ω ω )n ( , ,  = ( , 1 k k 1 2 ,  ω , ) kn ，其中 k=1,2，…,L。 2 k ,则 L 个权重向量的任意线性组 210 L ∂ = ω 为第 k 种赋权法求出的权重向量， k ∂ 为线性组合系数。 ω ω k k = K * 1 式中， k 根据博弈论组合赋权思想，要寻找最优权重向量，即求取式(27 )中使 *ω 与权重向量集 (27) 中各权重向量离差极小化的线性组合系数，可表示为 min ∂ L  = 1 K ω ω − T i k k 由矩阵的微分性质可得式 28 的最优化一阶导数条件： 215 ∂ L  = 1 K ωω ωω = T T i i k i k (28) (29) 求解式 29 方程，即可得到线性组合系数 1 ∂ ∂ ( , , 2 ∂ , )L , 归一化处理后得 ∂ * k = k ∂ ∂ L K= 1 ,进而得到最终的组合权重为 k ω = 4 算例分析 L ∂ = 1 K * ω k k (30) 220 为了验证本文模型和算法的合理性与正确性，选用 IEEE-33 节点配电系统，为其进行分布式电源位置和容量的规划。IEEE33 节点配电测试系统如图 1 所示，该配电系统有 37 条普通支路，14 条运算支路，33 个节点，首节点(0)为平衡节点，首端基准电压为 12.66kV，三相功率准值取 10MVA，总负荷为 3.715MW+2.300Mvar。假设节点电压取值范围为 0.9-1.05 pu， DG 待选安装节点编号为 1-32，共 32 个，最大 DG 安装节点数为 3 个，最大 - 7 -

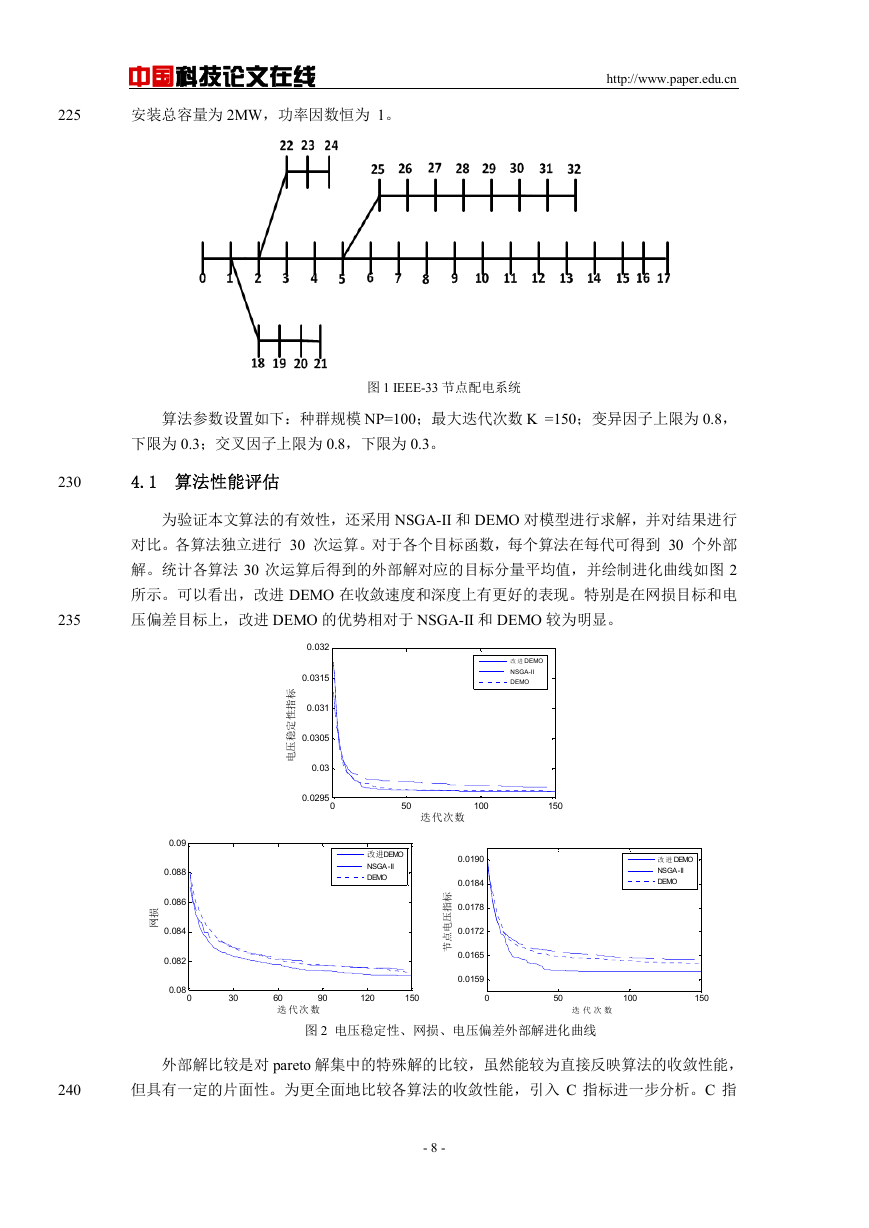
中国科技论文在线安装总容量为 2MW，功率因数恒为 1。 225 http://www.paper.edu.cn 图 1 IEEE-33 节点配电系统算法参数设置如下：种群规模 NP=100；最大迭代次数 K =150；变异因子上限为 0.8，下限为 0.3；交叉因子上限为 0.8，下限为 0.3。 230 4.1 算法性能评估为验证本文算法的有效性，还采用 NSGA-II 和 DEMO 对模型进行求解，并对结果进行对比。各算法独立进行 30 次运算。对于各个目标函数，每个算法在每代可得到 30 个外部解。统计各算法 30 次运算后得到的外部解对应的目标分量平均值，并绘制进化曲线如图 2 所示。可以看出，改进 DEMO 在收敛速度和深度上有更好的表现。特别是在网损目标和电压偏差目标上，改进 DEMO 的优势相对于 NSGA-II 和 DEMO 较为明显。 235 标指性定稳压电 0.032 0.0315 0.031 0.0305 0.03 0.0295 0 50 改进DEMO NSGA-II DEMO 0.09 0.088 0.086 0.084 0.082 损网 0.08 0 30 60 迭代次数 90 120 150 改进 DEMO NSGA-II DEMO 100 150 迭代次数标指压电点节 0.0190 0.0184 0.0178 0.0172 0.0165 0.0159 0 改进 DEMO NSGA-II DEMO 50 100 150 迭代次数图 2 电压稳定性、网损、电压偏差外部解进化曲线外部解比较是对 pareto 解集中的特殊解的比较，虽然能较为直接反映算法的收敛性能，但具有一定的片面性。为更全面地比较各算法的收敛性能，引入 C 指标进一步分析。C 指 240 - 8 -

资料库

分布式电源并网的多目标规划与决策研究.pdf

相关推荐

开发技术

热门标签

最新资料