logo资料库

基于二阶锥规划的有源配电网SNOP电压无功时序控制方法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.52M 资料格式：pdf 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    中国科技论文在线 http://www.paper.edu.cn 基于二阶锥规划的有源配电网 SNOP 电压 无功时序控制方法# 赵金利1，李雨薇1，李鹏1，冀浩然1，于浩2，王成山1，吴建中3** （1. 天津大学智能电网教育部重点实验室，天津市 300072； 2. 国网天津市电力公司检修公司，天津市 300230； 3. 卡迪夫大学工程学院，英国卡迪夫市 CF24 3AA） 摘要：分布式电源的广泛接入加剧了配电网的电压波动，与传统的负荷变化相比，由其引起 的电压变化在时间尺度上更为迅速，但传统的电压无功控制因其调节手段的限制不能实现快 速的实时调节。智能软开关（soft normally open point, SNOP）是一种代替传统联络开关可进 行实时调节的电力电子装置，在正常运行时主要提供有功功率的传递，当存在电压越限的情 况时，SNOP 可进行电压无功调节。首先建立了 SNOP 电压无功控制问题的时序模型，该模 型数学上属于大规模非线性规划问题，对问题的求解具有较大的挑战；进而提出了一种将 SNOP 电压无功时序控制模型转化为二阶锥可解形式的方法，使其能够实现该类大规模非线 性规划问题的快速、准确求解；最后，利用 IEEE 33 节点算例，对本文所提出的电压无功控 制模型与求解方法进行了分析与验证。 关键词：有源配电网；分布式电源；智能软开关（SNOP）；电压无功时序控制；二阶锥规 划 中图分类号：TM732 5 10 15 20 Sequential Voltage Regulation of Soft Normally Open Point in Active Distribution Network Based on Second-order Cone Programming 25 ZHAO Jinli1, LI Yuwei1, LI Peng1, JI Haoran1, YU Hao2, WANG Chengshan1, WU Jianzhong3 (1. Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin 300072; 2. Tianjin Electric Power Maintenance Company, Tianjin 300230; 3. School of Engineering, Cardiff University, Cardiff CF24 3AA) 30 35 40 Abstract: The integration of distributed generation (DG) exacerbates the voltage fluctuations of distribution network. Compared with the traditional load, voltage variation caused by DG is faster. However, the traditional voltage regulation means limited by the equipment constrains cannot realize fast real-time adjustment. Soft normally open point (SNOP) refers to a novel power electronic device with real-time adjustment capability installed in place of a tie switch, responsible for active power transfer in normal conditions and for voltage regulation in the case of voltage violation. Firstly, sequential voltage regulation model of SNOP is established, and its mathematical essence is a nonlinear optimization problem, bringing a challenge for solving the problem. Secondly, a method is proposed for changing the model into a solvable form by second-order cone programming (SOCP), quickly solving this kind of large-scale nonlinear optimization problems. Finally, case studies on IEEE 33-node test feeder analyse and verify the voltage regulation model and solving method proposed. Key words: active distribution network; distributed generator; soft normally open point (SNOP); sequential voltage regulation; second-order cone programming 基金项目：国家自然科学基金（51307116）；教育部博士点基金（20120032130008） 作者简介：赵金利（1979-），女，博士，副教授，主要研究方向：电力系统安全性与稳定性 通信联系人：李鹏（1981-），男，博士，副教授，主要研究方向：电力系统电磁暂态仿真与分布式发电技 术. E-mail: lip@tju.edu.cn - 1 -
    中国科技论文在线 http://www.paper.edu.cn 45 0 引言 配电网作为电力系统直接面向用户的一环，与用户的联系最为紧密，对用户的影响最为 直接。在我国电力体制改革的大背景下国家与社会的多方资本都将参与到配用电系统的升级 与改造中来，旨在提高绿色可再生能源发电的比重、电力交易的市场化水平、提升系统运行 的灵活性与开放性、保证供电质量与客户服务体验。从一次系统看，大量分布式能源接入配 50 电系统后将显著改变中低压层面电力系统的结构与运行方式[1][2]，使配电系统从传统的辐射 型网络发展为有源配电网[3][4]。 分布式能源渗透率的不断提高使有源配电网的潮流、无功与电压控制[5]等问题更加突 出，而用户侧多样化的发电、用电需求以及与网侧的灵活互动机制则使有源配电网的能量流 动进一步复杂。尤其是风机、光伏等间歇式能源和电动汽车等新型负荷无论在时间还是空间 55 上都具有很强的不确定性，在运行中往往导致馈线功率大幅波动、馈线间功率不平衡、以及 电压波动越限等诸多问题，进而使得系统运行损耗增加、运行经济性下降、分布式能源消纳 水平降低、系统运行风险提升，在一些情况下甚至可能因过载而引发设备故障导致停运，造 成巨大的经济损失。文献[6-8]以网络重构作为有源配电网的调节手段，使其能在正常情况下 提供稳定、可靠的控制策略，并能在故障情况下提供自愈策略支持。文献[9]以电容器组为 60 调节手段进行电压无功控制，从而加强电网的稳定运行。文献[10]以有载调压变压器（on-load tap changer, OLTC）为调节手段，使其实现有源配电网运行成本最低的目的，并使电压水平 整体有所提高。然而，传统的变压器分接头调整、补偿电容器投切等控制方式的调整能力有 限、精度不足，而基于分段、联络开关的网络重构则更多的受到开关动作时间、动作寿命、 以及冲击电流等问题的限制，难以满足分布式能源频繁波动时有源配电网的高精度实时运行 65 优化需求。 智能软开关装置（soft normally open point，SNOP）是安装于传统联络开关（tie switch, TS） 处的一种新型智能配电装置[11]，它能够通过控制所连接两侧馈线的有功与无功功率来实现 改善电压水平和提高 DG 消纳能力的作用[12][13]。在正常运行时 SNOP 主要负责有功功率的 传递，而当配电网存在电压越限时，SNOP 可进行电压无功控制。当分布式电源(distributed 70 generator, DG)接入电网后，配电网的电压波动加剧，SNOP 的实时调节能力可以减少分布式 电源对配电网的冲击，及时消除电压越限，保证系统安全运行。因此，SNOP 在未来将作为 配电系统一个重要的电压无功控制手段。 由于 SNOP 的功率调节是连续变化的，其运行优化问题从单一的时间断面扩展为连续的 时间序列，必须要以有效的时序运行优化模型作为优化问题的求解基础，为计算求解带来较 75 大的负担。与其它常见算法相比，二阶锥规划（second-order cone programming, SOCP）因其 求解速度快、寻优能力强而被广泛应用。该方法构建于支路潮流模型[14]的基础上，通过将 其中的二次等式作凸化松弛处理，并将非线性约束转化为 SOCP 可解的形式，将非凸非线性 问题转化为可高效求解的 SOCP 问题，从而可获得原问题的全局最优解。 本文以配电系统总损耗和电压越限加权之和最小为目标函数，以 SNOP 为控制手段，主 80 要进行电压无功控制，以保证配电网电压运行在期望水平，在此基础之上再尽可能降低系统 总损耗；然后提出一种将 SNOP 电压无功控制时序模型转化为 SOCP 可解形式的方法，使其 可以利用 SOCP 高效快速地求解此类大规模非线性优化问题；最后基于 IEEE 33 节点算例对 二阶锥模型转化方法的正确性与快速性进行测试，并在时序优化框架下，通过与优化前和网 络重构方案的对比，验证了 SNOP 在消除电压越限、减小电压偏差和降低系统损耗的作用。 - 2 -
    中国科技论文在线 http://www.paper.edu.cn 85 1 SNOP 电压无功控制问题的建模 1.1 SNOP 的结构和模型 SNOP 是基于全控型电力电子器件实现的，具体装置主要有 3 种：背靠背电压源型变流 器（back-to-back voltage source converter, B2B VSC）、统一潮流控制器（unified power flow controller, UPFC）和静止同步串联补偿器（static synchronous series compensator, SSSC）[11]。 本文以 B2B VSC 为例进行阐述，B2B VSC 可以精确控制馈线间传输的有功功率，并提供一 90 定的电压无功支撑。 图 1 SNOP 拓扑结构 Fig. 1 SNOP topological structure based on B2B VSC 95 对于一个 SNOP，其可控变量包括：两个变流器各自输出的有功功率 P1 和 P2，以及各 自输出的无功功率 Q1 和 Q2。由于变流器为电力电子器件，本身存在一定的有功损耗，因此 本文考虑 SNOP 的有功损耗。两个变流器的无功输出因直流环节的隔离而互不影响，仅需要 满足各自变流器的容量约束即可。本文选取 PQ-VdcQ 控制作为 SNOP 的控制模式。因此， SNOP 的运行控制需满足以下约束： 100 1）SNOP 传输的有功功率约束 2）SNOP 发出的无功功率约束 3）SNOP 容量限制 (1) (2) (3) 105 SNOP、Pt,j SNOP、Qt,i SNOP、Qt,j SNOP 分别为 t 时段 SNOP 在节点 i 与节点 j 的变流器输 式中，Pt,i 出的有功功率和无功功率，规定由大节点编号指向小节点编号的方向为 SNOP 有功传输与无 SNOP 分别为 SNOP 在节点 i 与节点 j 的变流器的有功损耗系数； 功补偿的正方向；Ai SNOP,max 分别为 t 时刻 SNOP 在节点 i 与节点 j 的变流器的 SNOP、Aj SNOP,max、Sj Si 接入容量和所能输出的无功功率上限。 SNOP,max、Qj SNOP,max、Qi 1.2 基于 SNOP 的电压无功控制时序模型 SNOP 电压无功时序控制方法通过控制有源配电网中 SNOP 的运行策略，实现兼顾配电 110 系统电压水平和网损的目的。本节提出基于 SNOP 的有源配电网电压无功控制时序模型。 1）目标函数 在正常运行时，SNOP 主要负责有功功率的传递，减小系统网络损耗；当存在电压越限 的情况时，SNOP 可进行电压无功控制。本文同时考虑配电系统网损与电压水平两个因素， 力求电压保持在期望水平的同时使网损最小。可表示为以下形式： - 3 - 变流器2bacbac变流器1交流系统1交流系统2SNOPSNOPSNOPSNOPSNOPSNOP,,,,0titjitijtjPPAPAPSNOP,maxSNOPSNOP,max,,,SNOP,maxSNOPSNOP,max,,,titititjtjtjQQQQQQSNOP2SNOP2SNOP,max,,SNOP2SNOP2SNOP,max,,()()()()titiitjtjjPQSPQS
    中国科技论文在线 http://www.paper.edu.cn (4) 115 式中，NN 为系统节点数；i 为节点 i 的相邻节点的集合；Rij 为支路 ij 的电阻；It,ij 为 t 时段 节点 i 流向节点 j 的电流有效值；Ut,i 为 t 时段节点 i 的电压有效值；和分别为配电系统 网络损耗和电压越限的权重系数；Uthr,max、Uthr,min 分别为节点电压幅值的优化区间上下限， 当 Ut,i Uthr,max 或 Ut,i Uthr,min 时，发生电压越限的情况，此时会通过电压无功控制使电压偏 差最小化。 120 在此基础上，考虑如下的系统运行约束： 1）系统潮流约束 (5) (6) (7) (8) 式中，i 以节点 i 为末端节点的支路首端节点集合，i 以节点 i 为首端节点的支路末端节点 集合；xij 为支路 ij 的电抗；Pt,ij、Qt,ij 分别为 t 时段节点 i 流向节点 j 的有功功率和无功功率； SNOP、 Pt,i、Qt,i 分别为 t 时段节点 i 上注入的有功功率和无功功率之和，Pt,i LOAD 分别为 t 时段节点 i 上分布式电源注入的有功功率和无功功率、SNOP 传输 SNOP、Qt,i LOAD、Qt,i DG、Qt,i DG、Pt,i 125 Pt,i 的有功功率和无功功率、负荷消耗的有功功率和无功功率。 2）运行电压水平约束 式中，Ui min和Ui max 分别为节点 i 的最小允许电压值和最大允许电压值。 3）支路容量约束 130 式中，Iij max 为节点 i 流向节点 j 的电流幅值上限。 4）辐射型拓扑运行结构 系统运行拓扑应满足无环、无孤岛的辐射状要求。 2 二阶锥模型转化 (9) (10) 含 SNOP 的电压无功控制时序模型为大规模非线性优化问题，为计算求解增加了较大的 135 难度。锥规划算法是线性空间中凸锥上的数学规划，其所具备的锥结构有助于算法的设计 [15]。因其具有求解速度快、寻优能力强的特点，被广泛应用于求解大规模非线性问题[16]。 本文依据锥规划算法的基本原理，对规划模型的目标函数与约束条件进行了锥模型转化，将 原问题转化为 SOCP 问题，使其不仅能快速实现问题的求解，还能保证所求解的最优性[17]。 SOCP 的标准形式如下[18]： (11) - 4 - NN22thr,maxthr,min,,,,11 min()|()1|:(||)iNNijtijtititiijifRIUUUUU2,,,,ΨΦ2,,,,ΨΦ()()iiiitiktjijitjitikjtiktjijitjitikjPPRIPQQXIQDGSNOPLOAD,,,DGSNOPLOAD,,,,,tititititittiitiPPPPQQQQ22,,2,2,(((())))tijtijtijtiQIUP22222,,,,,((((()=)2)))tjtiijtijijtijijijtijUUPRRXQIX,min22max2)((())itiiUUU2max2,0()()iijjtIITmin|,0KcxAxbx
    中国科技论文在线 http://www.paper.edu.cn 140 式中，K 为有限个非空尖凸锥的笛卡尔乘积，x 为 n 维决策变量。cTx 是决策变量 x 的线性 函数，Ax=b 表示线性约束，x K0 表示非线性约束。 2.1 目标函数的二阶锥模型转化 目标函数（4）中含有二次项(Ut,i)2 和(It,ij)2，采用 U2,t,i 和 I2,t,ij 替换二次项(Ut,i)2 和(It,ij)2， 将其线性化，如式（12）所示。 (12) 145 由于式（12）中含有绝对值项 ，引入辅助变量 ，并增加约束[19] (13) 2.2 约束条件的二阶锥模型转化 约束条件（5）~（10）中含有二次项(Ut,i)2 和(It,ij)2，采用 U2,t,i 和 I2,t,ij 替换二次项(Ut,i)2 和(It,ij)2，将其线性化，如式（14）~（17）所示[18]。 (14) (15) (16) (17) 约束条件（15）经上述变形后，根据文献[20,21]做一步松弛，如式（18）所示，再等价 150 变形成式（19）所示的标准二阶锥的形式。 约 束 条 件 （ 1 ） 中 含 有 绝 对 值 项 和 ， 引 入 辅 助 变 量 ，并增加约束： SNOP 运行约束条件（3）均为非线性约束，将其转换为旋转锥约束： - 5 - (18) (19) 和 (20) (21) (22) NNthr,max2thr,min22,,2,,2,,2,,11min1:(()||())NNijtijtititiijiifRIUUUUU2,,1tiU,2,,1titiAU,thr,max2,2,,thr,min2,2,,0()()tititititiAAUUAUU2,,,ΨΦ,,,ΨΦ,,2,, iiiitiktjijitikjtjittiktjijitijikjPPRPQQQIIX22,,2,,2,,()()tijtijtijtijPQIU222,,2,,,,2,,=2tjtjijtijijtijijijtijUURPXQRXI22,min,max22,2,,,,max0iititijijUUIIU22,,2,,2,,()()tijtijtijtijPQIUT,,2,,2,,2,,2,,222tijtijtijtitijtiPQIUIUSNOP,tiPSNOP,tjPSNOP,,titjMPSNOP,,tjtjMP,SNOP,,SNOP,,0tititititiMMPMP,SNOP,,SNOP,,0tjtjtjtjtjMMPMPSNOPSNOPSNOP,SNOP,,,0tijtjtitijPMPAMA
    中国科技论文在线 http://www.paper.edu.cn (23) 经过上述步骤的转化，分别将目标函数线性化，非线性约束转化为线性约束、二阶锥约 155 束或旋转锥约束。 3 算例分析 3.1 测试平台与算例系统 为了充分验证本文提出方法的正确性与有效性，在 Matlab 环境下通过 YALMIP[22]编程 并利用 CPLEX 算法包进行测试。执行优化计算的计算机硬件环境为 Intel(R) Xeon(R) CPU 160 E5-1620，主频为 3.70GHz，内存为 32GB；软件环境为 Windows 7 操作系统。 本文基于扩展的 IEEE 33 节点系统对算法进行测试，结构如图 2 所示[23]。IEEE 33 节点 系统包含 37 条支路，电压等级为 12.66kV，基准功率为 1MVA。设定 5 台风电机组的接入 位置为节点 10、16、17、30、33，接入容量分别为 300kVA、200kVA、200kVA、200kVA、 300kVA，功率因数均为 0.9；3 台光伏系统的接入位置为节点 7、13、27，接入容量分别为 165 500kVA、300kVA、400kVA，功率因数均为 0.9；5 个 SNOP 的两个变流器有功功率区间均 为-500~500kW，无功功率区间均为 0~850kVar，损耗系数为 0.005。节点电压幅值的优化区 间上下限为 0.98~1.02，所有超出这个范围的电压幅值，其对应的节点将进行电压优化。 170 图 2 IEEE 33 节点算例 Fig. 2 IEEE 33-node test feeder 在式（4）所示的目标函数中，有配电系统网络损耗的权重系数和电压越限的权重系 数。将成对比较矩阵应用到层次分析法（Analytic Hierarchy Process，AHP）中，得到=0.83， =0.17[17]。 3.2 算法准确性验证 175 分别采用基于内点法求解原始非线性规划（nonlinear programming, NLP）模型的方法和 基于二阶锥规划的 SNOP 电压无功时序控制的方法对 IEEE 33 节点系统的节点 18 和 33 之间 接入 1 个 SNOP 的情况进行计算，前者使用 IPOPT 工具进行计算，后者使用 CPLEX 算法包 进行计算。采用上述两种方法获得的结果如表 1 所示。可以看出，两种方法得到的结果基本 一致，说明 SOCP 模型转化是精确的，而在求解时间上，基于 CPLEX 软件的二阶锥规划算 180 法比基于 IPOPT 工具的内点法要明显快速。 表 1 NLP 模型和 SOCP 模型的计算结果 Tab. 1 Results of NLP model and SOCP model - 6 - SNOP,maxSNOPSNOP,maxSNOP,2SNOmaxSNOP,maxP2,,SNOP2SNOP2,,()()22(2(222))iijtititjtjjSSPPQSQS187654329101112131415161718192021222324252627282930313233TS2TS5TS3TS1PVWTWTPVPVWTWTWTTS4
    中国科技论文在线 http://www.paper.edu.cn 算法 内点法 锥规划 网损/kW 22.2808 22.6471 电压偏差/p.u, 0.2063 0.0001 目标函数值/p.u. 0.0536 0.0188 求解时间/s 389.18 0.01 按照前文所述的二阶锥规划算法，可得到其准确性验证公式，如式（24）所示，由此可 185 验证 SNOP 优化前与优化后两种方案用本文所述锥规划算法松弛后是否可得到正确的结果。 每个节点的松弛偏差量 Δd 值都很小，为 10-9 量级左右，从而再一次验证了本文所提出算法 是严格而准确的。 (24) 3.3 多种方案下算例测试结果 由于在实际运行中需要对配电网进行快速调节，因此对上述 IEEE 33 节点算例进行时序 优化。如果考虑时序情况，则负荷日运行曲线可以利用负荷预测方法获得并取 1 小时为一个 190 点，风电、光伏发电处理方式相同，无功功率由功率因数获得。整个系统的分布式电源出力 和负荷的功率变化情况如图 3 所示。 图 3 分布式电源与负荷日功率曲线 Fig. 3 Power curves of the DG and loads 195 为了更好地体现 SNOP 在电压无功控制方面较联络开关的优势，以及不同数量的 SNOP 的接入所带来的不同优化效果，本文将在 24 断面下对优化前的情况和所选取的 4 种优化方 案仿真，并进行对比分析。仿真结果如图 4 所示。 方案 1：不采用 SNOP，基于网络重构进行运行优化和电压控制[24]，其中 5 个 TS 的接 入位置、编号如图 2 所示。 200 方案 2：1 个 SNOP 接入算例系统，取代图 2 中的 TS2，进行运行优化和电压控制。 方案 3：2 个 SNOP 同时接入算例系统，取代图 2 中的 TS1 和 TS2，进行运行优化和电 压控制。 方案 4：5 个 SNOP 同时接入算例系统，取代图 2 中全部的 TS，进行运行优化和电压控 制。 205 在实际运行中，TS 由于其动作涉及到开关的使用寿命、合环电流冲击等因素，故而很 难做到实时调节，因此本文假定网络重构每天执行一次。 - 7 - T,,2,,2,,2,,2,,222()tijtijtijtitijtidPQIUIU012345678910111213141516171819202122232405001000150020002500300035004000时间/h有功功率/kW 光伏发电风力发电负荷
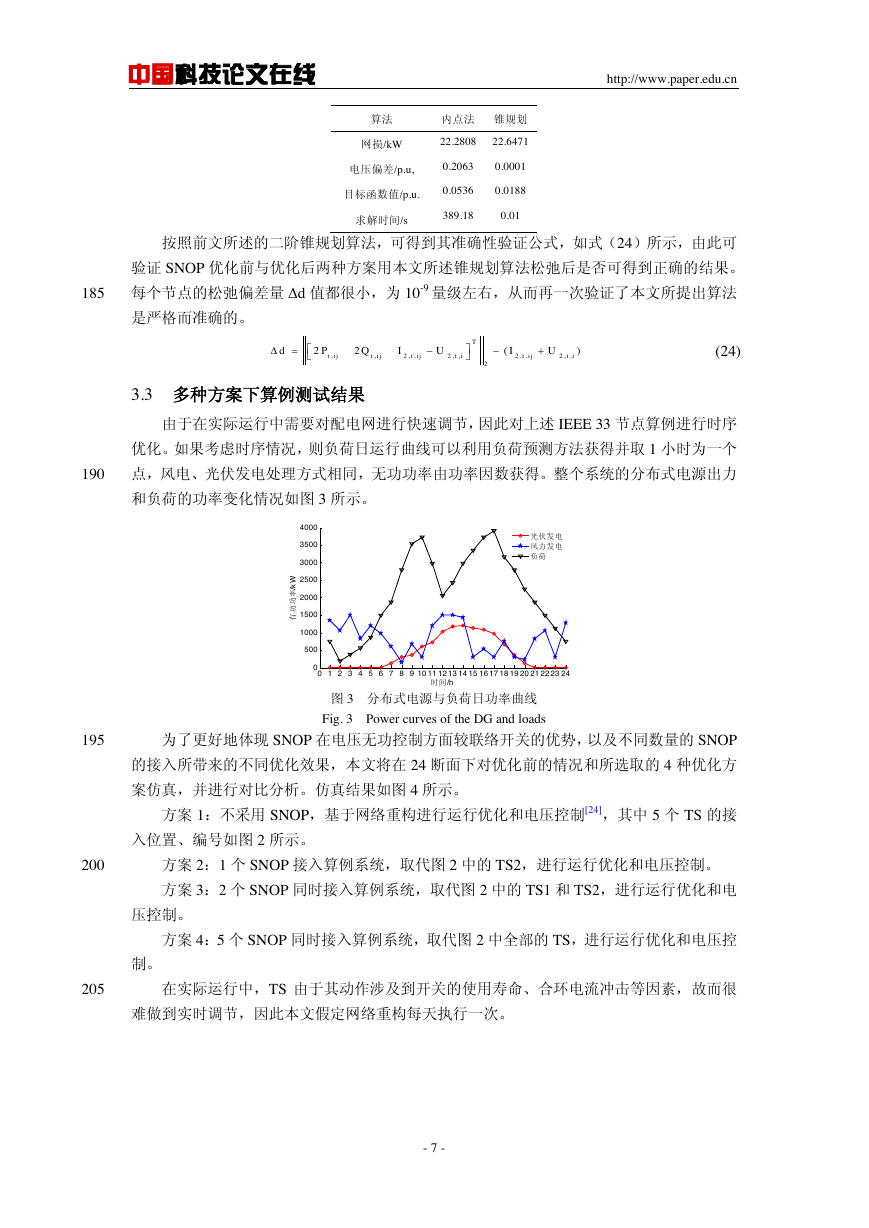
    中国科技论文在线 http://www.paper.edu.cn (a)节点 18 电压幅值 210 (b)节点 33 电压幅值 (c)不同方案下的系统有功损耗情况 图 4 时序条件下不同方案的优化结果 Fig. 4 Sequential optimization results of different scenarios 215 由于优化方案的不同，各节点电压呈现出不同的优化水平，如图 4(a)、图 4(b)所示。可 以看出，由于分布式电源的接入，优化前电压幅值波动剧烈，且电压偏移情况较为剧烈。方 案 1 所采用的网络重构方法缩小了电压波动的剧烈程度，但却不能总是很好地将节点电压控 制在目标水平 0.98~1.02 之间或附近。而采用 SNOP 进行电压无功控制则可更为有效地缩小 电压波动的剧烈程度，减小电压偏移，并且能够更好地将节点电压幅值控制在目标水平 220 0.98~1.02 附近。以图 5 为例，算例系统中接入的风电和光伏使得该系统电压发生较大波动， 当负荷较大、DG 出力较小时，SNOP 向系统提供一定的无功功率，并由节点 33 向节点 18 传输一定的有功功率，以平衡整个系统有功功率与无功功率的分配情况，进而改善系统的电 压水平，降低网损；当负荷较小、DG 出力较大时，SNOP 停止向系统提供无功支撑，节点 18 向节点 33 传输一定的有功功率，同样改善系统运行状态。比较方案 2、3、4 可知，随着 225 SNOP 接入个数的增多，电压改善情况越来越明显，当系统同时接入 5 个 SNOP 时，电压改 善情况最好，节点电压幅值基本控制在电压目标值 0.98~1.02 之间。因此，SNOP 改善电压 水平的能力很强，并且这个能力会随着 SNOP 接入个数的增多而变得更强，但新接入的 SNOP 改善电压的效果却在下降，因此考虑到经济问题，还需对 SNOP 接入个数及位置进行进一步 研究。 - 8 - 01234567891011121314151617181920212223240.940.960.9811.021.041.06时间/h电压/p.u. 不优化方案1方案2方案3方案401234567891011121314151617181920212223240.920.940.960.9811.021.04时间/h电压/p.u. 不优化方案1方案2方案3方案4不优化方案1方案2方案3方案402004006008001000有功损耗/(kW)
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料