随机信号生成.doc

发布时间：2022-06-15 发布人：admin 分类：说明书资料大小：0.12M 资料格式：doc 举报版权申诉

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第1页.png

第1页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第2页.png

第2页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第3页.png

第3页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第4页.png

第4页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第5页.png

第5页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第6页.png

第6页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第7页.png

第7页 / 共13页

5d76c19d-fa45-44fb-94b0-fefc914351be.doc.pdf-第8页.png

第8页 / 共13页

文本预览

通信原理仿真姓名：郭耀川学号：12041077 班级：信息 3 班

1.Gaussian distributed random variates, draw the corresponding，PDFs(histograms) for N( , obtained. 2) be N(0,1), N(0,4.26), and N(-2.5,1) by using the random variates 相关代码 #include double uniform(double a,double b,long int *seed) {double t; *seed=2045*(*seed)+1; *seed=*seed-(*seed/1048576)*1048576; t=(*seed)/1048576.0; t=a+(b-a)*t; return(t); } double gauss(double mean,double std,long *s) {int i; double x=0.0,y=0.0; for(i=0;i<12;i++) {x=x+uniform(0.0,1.0,s);} x=x-6.0; y=mean+std*x; return y; } void main() {double mean=0.0,std=1.0,y; int i,j; long s=13579; scanf("%lf %lf",&mean,&std); FILE *fp=fopen("c:\\data.txt","w"); for(j=0;j<5000;j++) {y=gauss(mean,std,&s); printf("%13.7f",y); fprintf(fp,"%13.7f",y); }

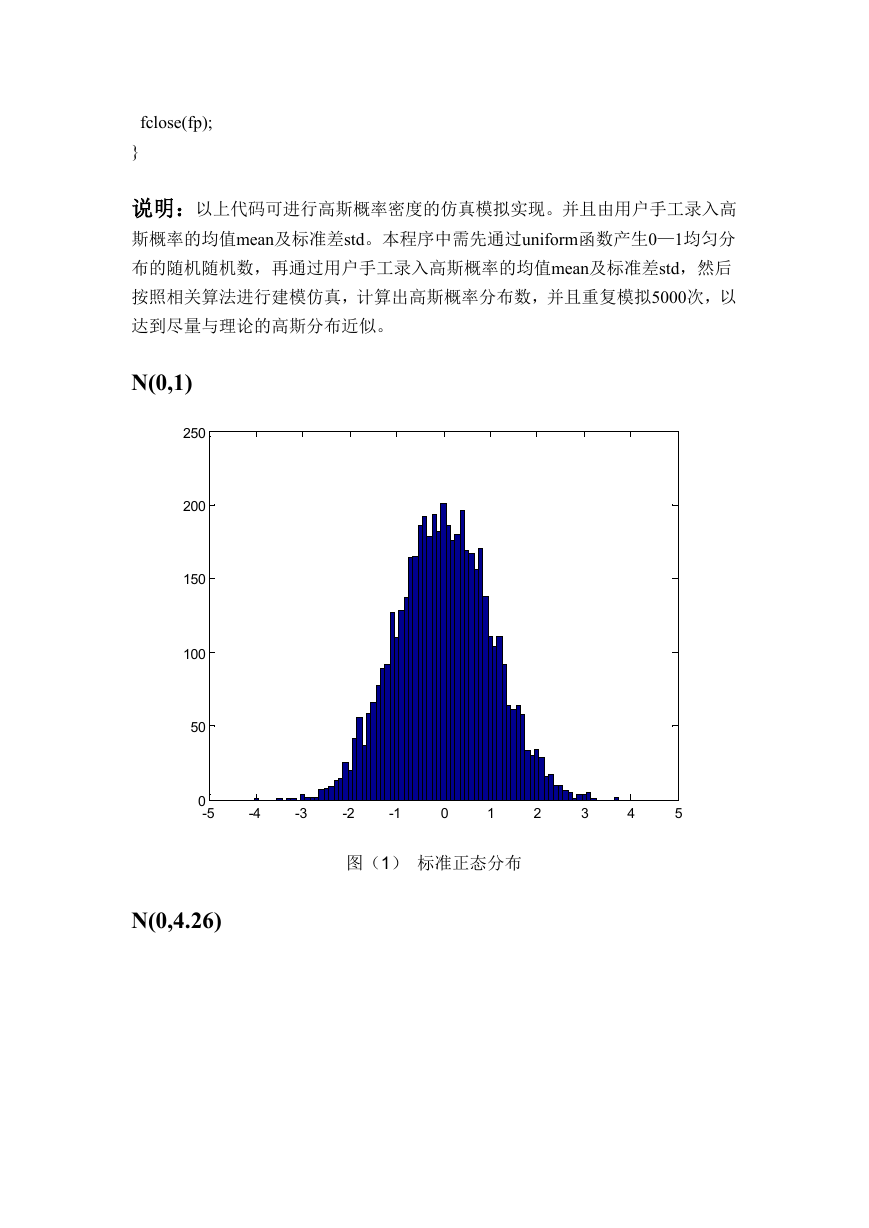
fclose(fp); } 说明：以上代码可进行高斯概率密度的仿真模拟实现。并且由用户手工录入高斯概率的均值mean及标准差std。本程序中需先通过uniform函数产生0—1均匀分布的随机随机数，再通过用户手工录入高斯概率的均值mean及标准差std，然后按照相关算法进行建模仿真，计算出高斯概率分布数，并且重复模拟5000次，以达到尽量与理论的高斯分布近似。 N(0,1) 250 200 150 100 50 0 -5 N(0,4.26) -4 -3 -2 -1 0 1 2 3 4 5 图（1）标准正态分布

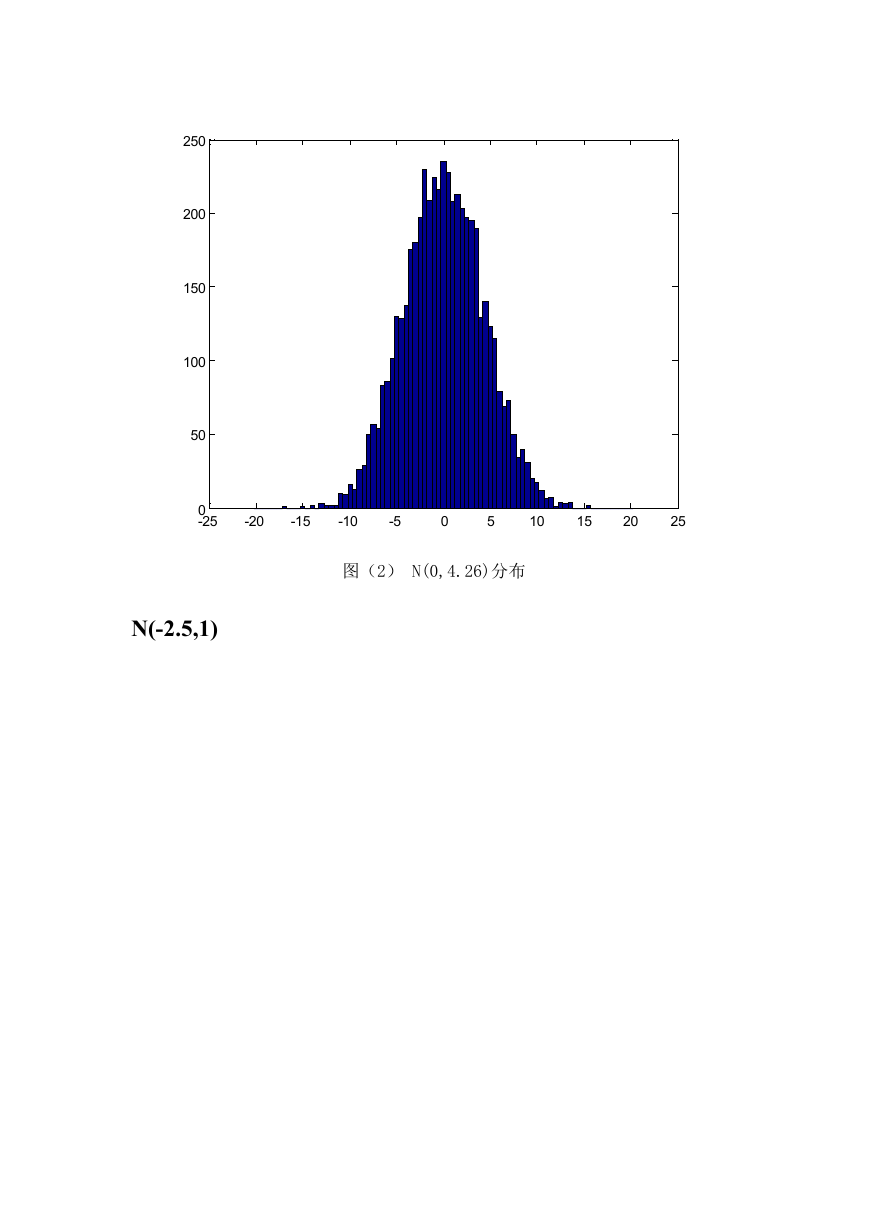
250 200 150 100 50 0 -25 -20 -15 -10 -5 0 5 10 15 20 25 图（2） N(0,4.26)分布 N(-2.5,1)

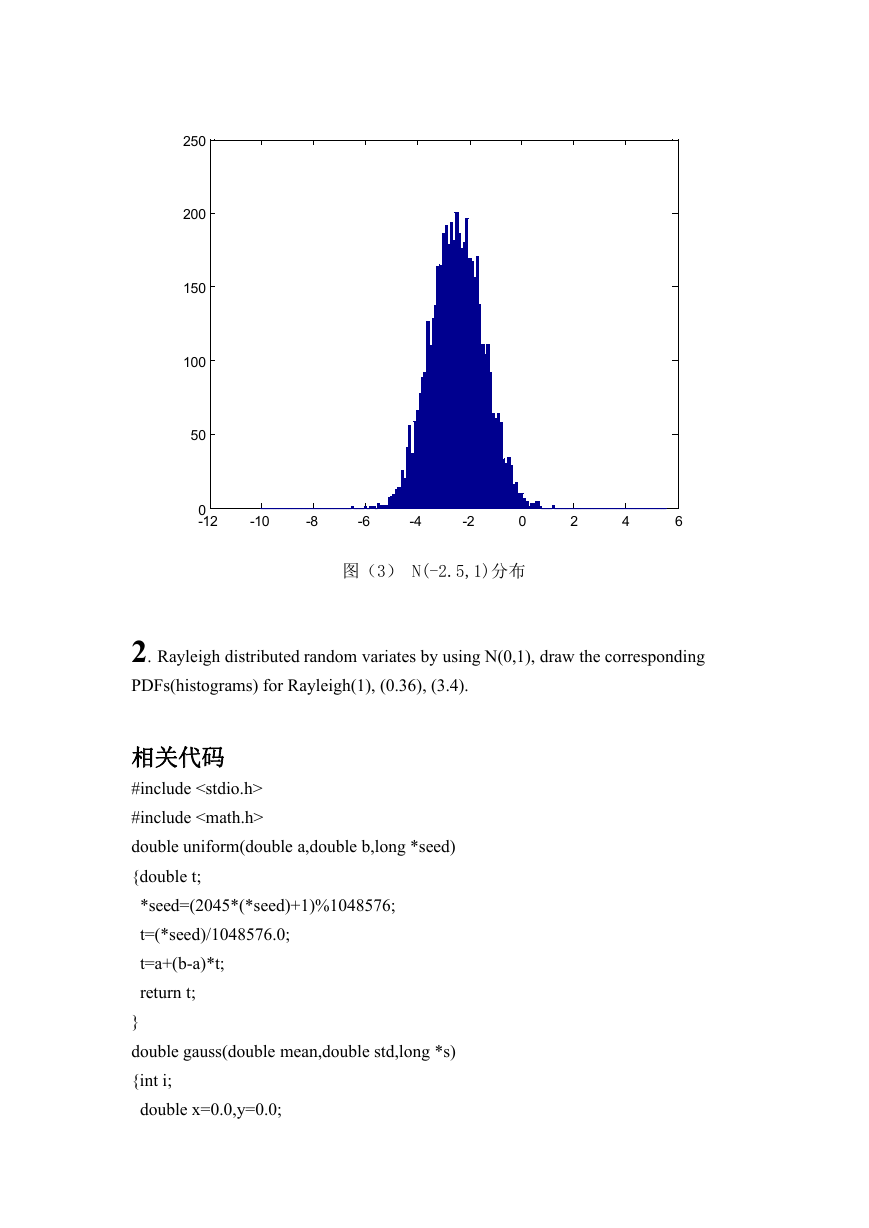
250 200 150 100 50 0 -12 -10 -8 -6 -4 -2 0 2 4 6 图（3） N(-2.5,1)分布 2. Rayleigh distributed random variates by using N(0,1), draw the corresponding PDFs(histograms) for Rayleigh(1), (0.36), (3.4). 相关代码 #include #include double uniform(double a,double b,long *seed) {double t; *seed=(2045*(*seed)+1)%1048576; t=(*seed)/1048576.0; t=a+(b-a)*t; return t; } double gauss(double mean,double std,long *s) {int i; double x=0.0,y=0.0;

for(i=0;i<12;i++) {x=uniform(0.0,1.0,s)+x;} x=x-6.0; y=mean+std*x; return y; } void main() {double mean=0.0,std=1.0,y1,y2,y; int i,j; long s1=56789,s2=12345; scanf("%lf",&std); FILE *fp=fopen("c:\\data1.txt","w"); for(j=0;j<5000;j++) {y1=gauss(mean,std,&s1); y2=gauss(mean,std,&s2); y=sqrt(y1*y1+y2*y2); printf("%13.7f",y); fprintf(fp,"%13.7f",y); } fclose(fp); } 说明：以上代码可进行瑞利概率密度的仿真模拟实现。本程序中需先通过 uniform函数产生0—1均匀分布的随机随机数，再通过guass函数模拟出符合高斯概率分布的高斯数，最后利用上一步得出的高斯数计算得出瑞利分布数，并且重复模拟5000次，以达到尽量与理论的瑞利分布近似。 Rayleigh(1)

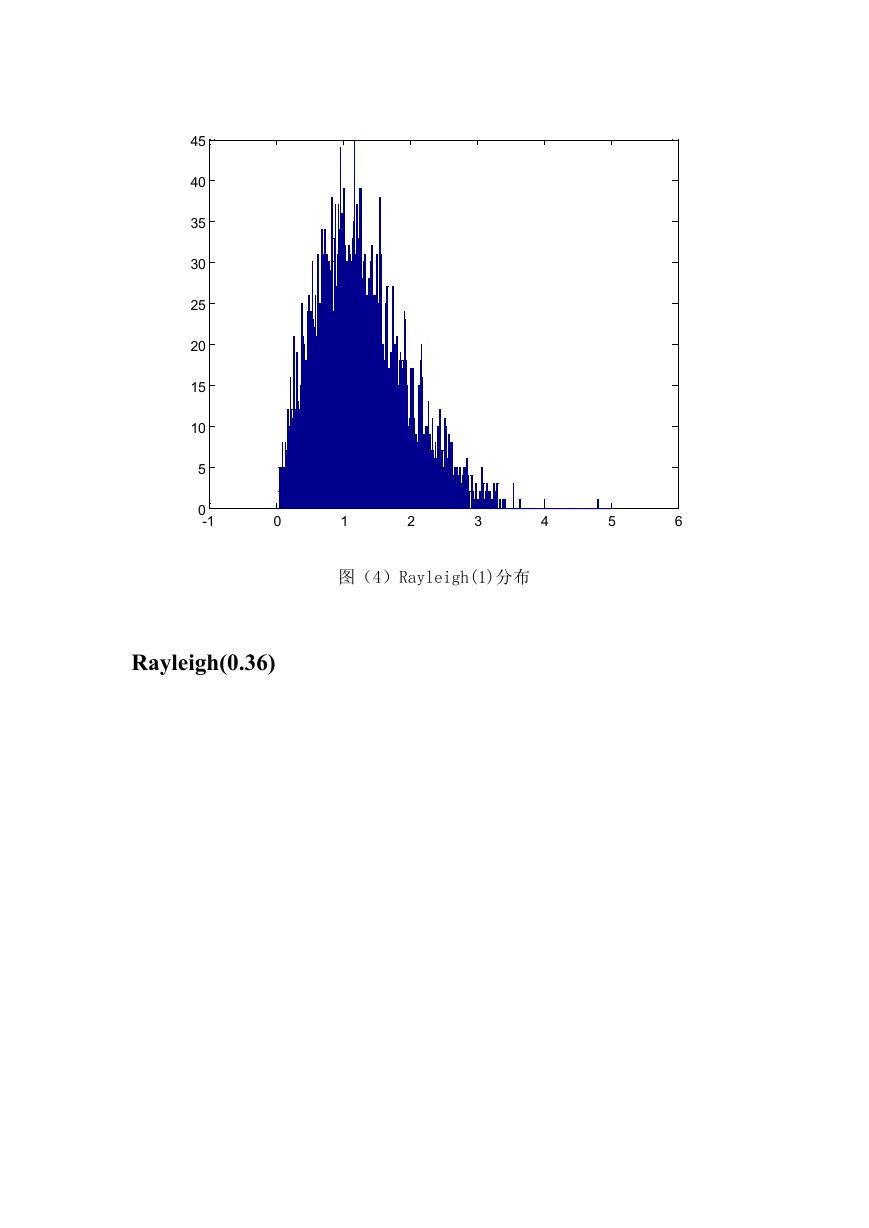
45 40 35 30 25 20 15 10 5 0 -1 0 1 2 3 4 5 6 图（4）Rayleigh(1)分布 Rayleigh(0.36)

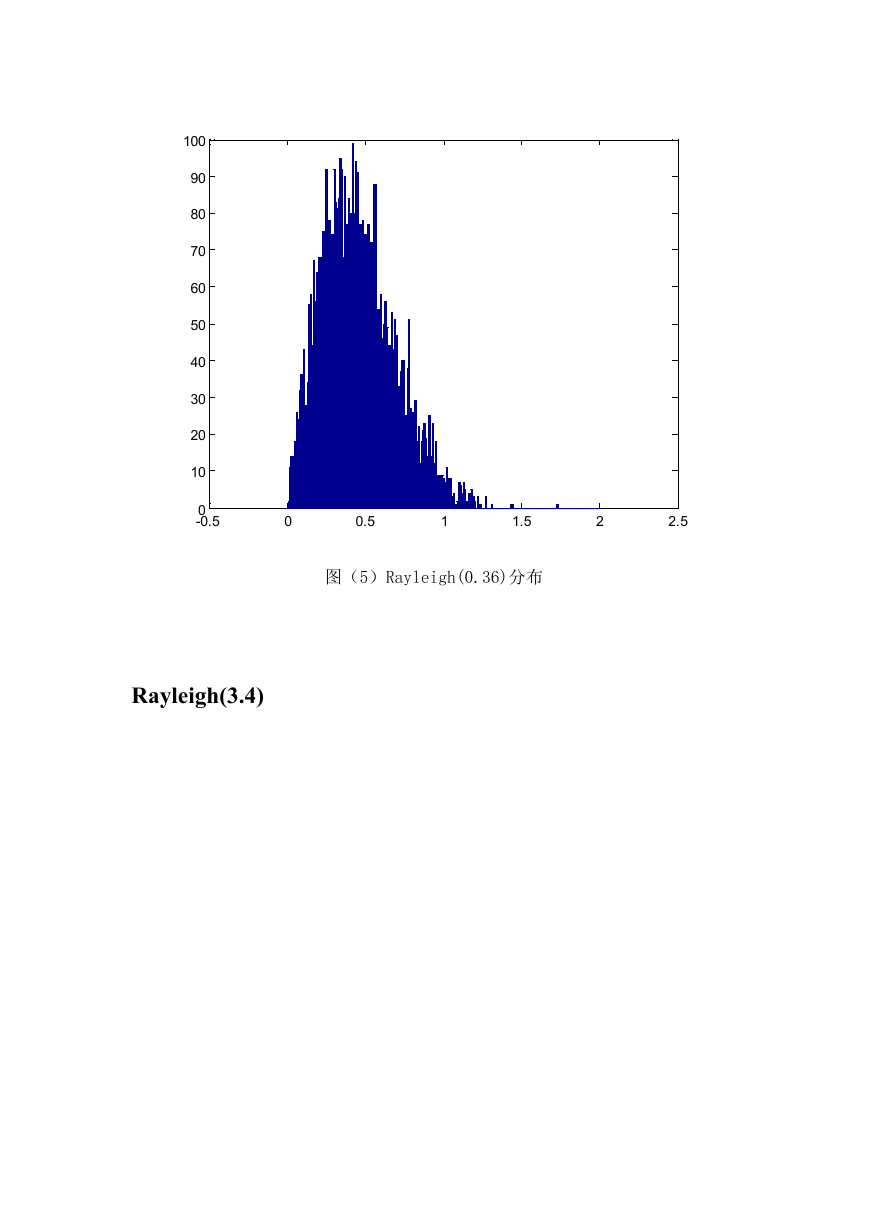
100 90 80 70 60 50 40 30 20 10 0 -0.5 Rayleigh(3.4) 0 0.5 1 1.5 2 2.5 图（5）Rayleigh(0.36)分布

分享到：

赞收藏

资料库

随机信号生成.doc

相关推荐

后端

热门标签

最新资料