5GFBMC调制模式介绍文档.pdf-资料库

PHYDYAS 06/2010 1 M.Bellanger on behalf of the participants: CNAM: M.Bellanger, D.LeRuyet, D.Roviras, M.Terré TUM: J.Nossek, L.Baltar, Q.Bai, D.Waldhauser TUT: M.Renfors, T.Ihalainen, A.Viholainen, T.H.Stitz UCL: J.Louveaux, A.Ikhlef SINTEF: V.Ringset, H.Rustad CTTC: M.Najar, C.Bader, M.Payaro RA-CTI: D. Katselis, E. Kofidis, L. Merakos, A. Merentitis, N. Passas, A. Rontogiannis, S. Theodoridis, D. Triantafyllopoulou, D. Tsolkas, D. Xenakis UNINA: M.Tanda, T.Fusco CEA-LETI: M.Huchard AGILENT : J.Vandermot ALCATEL-LUCENT/UK : A.Kuzminskiy ALCATEL-LUCENT/DE : F.Schaich COMSIS : P.Leclair, A.Zhao FBMC physical layer : a primer Summary: The filter bank multicarrier (FBMC) transmission technique leads to an enhanced physical layer for conventional communication networks and it is an enabling technology for the new concepts and, particularly, cognitive radio. The objective of this document is to provide an overview of FBMC, with emphasis on the features which impact communication networks. The only prerequisite for reading the document is basic knowledge in digital signal processing, in particular sampling theory, fast Fourier transform (FFT) and finite impulse response (FIR) filtering. More thorough developments on the techniques described, as well as alternative and more sophisticated methods, are available on the website http://www.ict-phydyas.org . The presentation begins with to multicarrier communications, pointing out the limitations of this simplistic approach, and, particularly, the spectrum leakage. Then, it is shown that the FFT approach can evolve to a filter bank approach which is straightforward to design and implement. For each block of data, the time window is extended beyond the multicarrier symbol period and the symbols overlap in the time domain. This time overlapping is at the basis of conventional efficient single carrier modems where interference between the symbols is avoided if the channel filter satisfies the Nyquist criterion. This fundamental principle to multicarrier transmission. Regarding implementation, the filter bank approach is just an extension of the direct FFT approach and it can be realized with an extended FFT. An alternative scheme, the direct application of the FFT is readily applicable 1

PHYDYAS 06/2010 2 requiring less computations, is the so-called polyphase network (PPN)-FFT technique, which keeps the size of the FFT but adds a set of digital filters. Contrary to OFDM (orthogonal frequency division multiplexing) where orthogonality must be ensured for all the carriers, FBMC requires orthogonality for the neighbouring sub-channels only. In fact, OFDM exploits a given frequency bandwidth with a number of carriers, while FBMC divides the transmission channel associated with this given bandwidth into a number of sub-channels. In order to fully exploit the channel bandwidth, the modulation in the sub- channels must adapt to the neighbour orthogonality constraint and offset quadrature amplitude modulation (OQAM) is used to that purpose. The combination of filter banks with OQAM modulation leads to the maximum bit rate, without the need for a guard time or cyclic prefix as in OFDM. The effects of the transmission channel are compensated at the sub-channel level. The sub- channel equalizer can cope with carrier frequency offset, timing offset and phase and amplitude distortions, so that asynchronous users can be accomodated. When FBMC is employed in burst transmission, the length of the burst is extended to allow for initial and final transitions due to the filter impulse response. These transitions may be shortened if some temporary frequency leakage is allowed, for example whenever a frequency gap is present between neighbouring users. As a multicarrier scheme, FBMC can benefit from multiantenna systems and MIMO techniques can be applied. Due to OQAM modulation, adaptations are necessary for some MIMO approaches, in the diversity context. FBMC systems are likely to coexist with OFDM systems. Since FBMC is an evolution of OFDM, some compatibility can be expected. In fact, the initialization phase can be common to both and efficient dual mode implementation can be realized. In the multiuser context, the sub-channels or groups of sub-channels allocated to the users are spectrally separated as soon as an empty sub-channel is present in-between. Therefore, users do not need to be synchronized before they gain access to the transmission system. This is a crucial facility for uplink in base station ruled networks or for future opportunistic communications. In cognitive radio, the FBMC technique offers the possibility to carry out the functions of spectrum sensing and transmission with the same device, jointly and simultaneously. Moreover, the users enjoy a guaranteed level of spectral protection. 2

PHYDYAS 06/2010 3 Contents: Summary 1) The FFT as a multicarrier modulator 2) Filtering effect of the FFT 3) Prototype filter design - Nyquist criterion 4) Extending the FFT to implement the filter bank 5) PPN-FFT to reduce computational complexity 6) OQAM modulation 7) Effects of the transmission channel 8) Sub-channel equalization 9) Burst transmission with FBMC 10) MIMO-FBMC 11) Compatibility with OFDM 12) FBMC in networks Phydyas website 3

PHYDYAS 06/2010 4 P / S di(mM) iFFT 1. The FFT as a multicarrier modulator The inverse fast Fourier transform (iFFT) can serve as a multicarrier modulator and the fast Fourier transform (FFT) can serve as a multicarrier demodulator. A multicarrier transmission system is obtained and the transmitter and the receiver are shown in Fig.1. Fig.1. Multicarrier modulation with the FFT It is obvious from the figure that the block of data at the input of the iFFT in the transmitter is recovered at the output of the FFT in the receiver, since the FFT and the iFFT are cascaded. The detailed description of the operations is as follows. The size of the iFFT and the FFT is M and a set of M data samples, 0 by with the iFFT output is expressed , is fed to the iFFT input. For FFT di((m-1)M) transmitter Mmn ( + receiver (mMdi ≤≤ Mi x(n) S / P <≤ mM )1 − 1 ) x n ( ) d mM e π ( ) 2 j i i n mM ( − M ) M 1 − = ∑ i = 0 The set of M samples so obtained is called a multicarrier symbol and m is the symbol index. For transmission in the channel, a parallel-to-serial (P/S) converter is introduced at the output x n appear in serial form. The sampling frequency of the of the iFFT and the samples ( ) transmitted signal is unity, there are M carriers and the carrier frequency spacing is 1/M. The duration of a multicarrier symbol T is the inverse of the carrier spacing, T=M. Note that T is also the multicarrier symbol period, which reflects the fact that successive multicarrier symbols do not overlap in the time domain. x n is a ( ) An illustration is given in Fig.2 for 2 is transmitted by i i = periods. Similarly, sine wave and the duration T contains periods of a sine wave in the duration T . Overall, the transmitted signal is a collection of sine waves such that the symbol duration contains an integer number of periods. In fact, it is the condition for data recovery, the so-called orthogonality condition. At the receive side, a serial-to-parallel (S/P) converter is introduced at the input of the FFT. The data samples are recovered by . The transmitted signal i = and 2 mMd (2 (mMdi ±= 1 ) ) mMd i ( ) = 1 M mM 1 + M ∑ − mMn = − j enx )( 2 π mMni ( − M ) Note also in Fig.1 that, due to the cascade of P/S and S/P converters, there is a delay of one multicarrier symbol at the FFT output with respect to the iFFT input. 4

PHYDYAS 06/2010 5 T A +1 -1 d2(mM) Real(x(n)) Fig.2. Data and transmitted signals For the proper functioning of the system, the receiver (FFT) must be perfectly aligned in time with the transmitter (iFFT). Now, in the presence of a channel with multipath propagation, due to the channel impulse response, the multicarrier symbols overlap at the receiver input and it is no more possible to demodulate with just the FFT, because intersymbol interference has been introduced and the orthogonality property of the carriers has been lost. Then, there are 2 options: d2((m-1)M) time 1) extend the symbol duration by a guard time exceeding the length of the channel impulse response and still demodulate with the same FFT. The scheme is called OFDM. 2) keep the timing and the symbol duration as they are, but add some processing to the FFT. The scheme is called FBMC, because this additional processing and the FFT together constitute a bank of filters. The present document is concerned with this second approach and, as an introduction, it will first be shown that the FFT itself is a filter bank. 2. Filtering effect of the FFT Let us assume that the FFT is running at the rate of the serially transmitted samples. Considering Fig.1, the relationship between the input of the FFT and the output with index 0=k is the following x n M [ ( x n ( 1)] .... = − + + − = ) ) y n ( ) 0 1 M M = i 1 −∑ x n i ( 1 M This is the equation of a low-pass linear phase FIR filter with the M coefficients equal to M/1 . 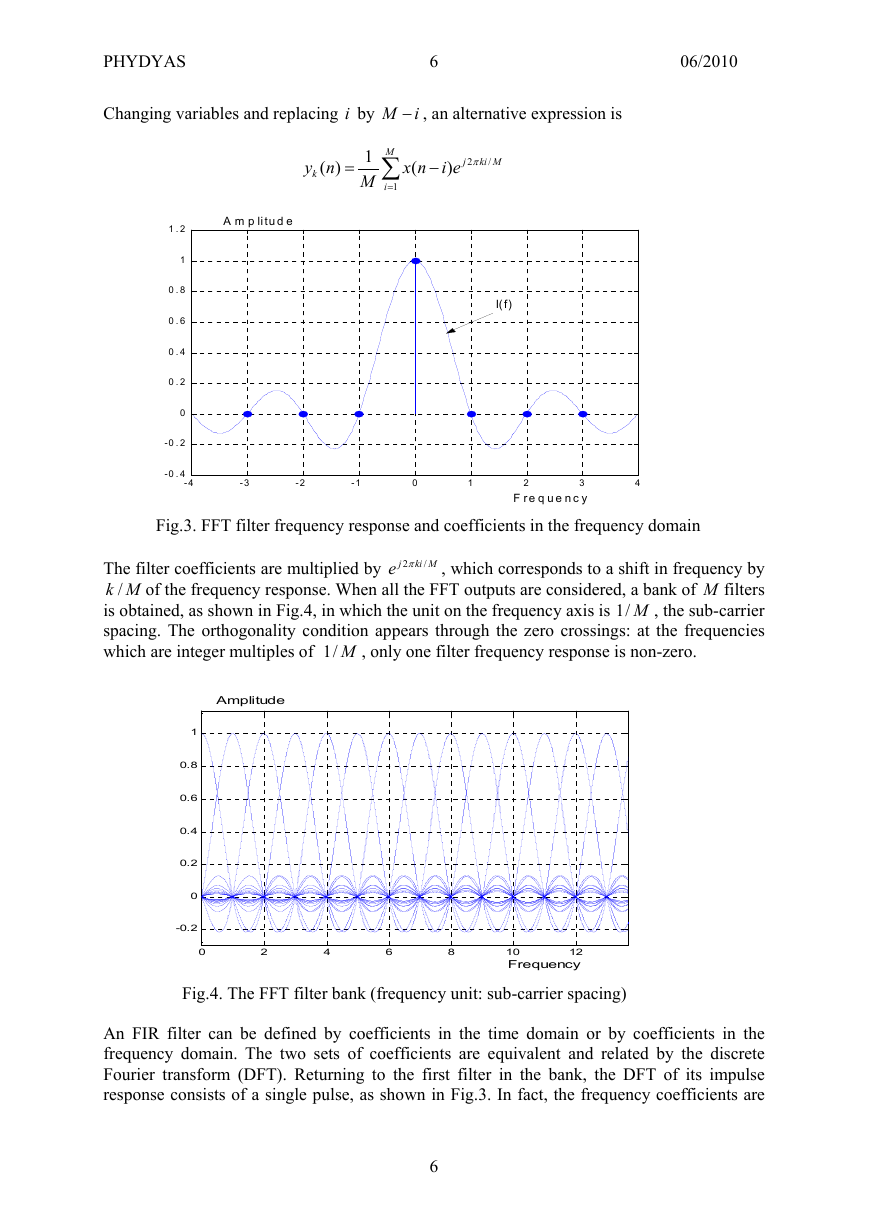Disregarding the constant delay, the frequency response is = I ( ) f sin M π sin fM f π It is shown in Fig.3, where the unit on the frequency axis is 1/M. In the same conditions, the FFT output with index k is expressed by x n M i e ( ) ki M 2 π = − + 1 − M − j / y n ( ) k 1 M ∑ i = 0 5

PHYDYAS 06/2010 6 4 / Changing variables and replacing i by M i− , an alternative expression is x n i e ( ) ki M 2 π = M j / y n ( ) k 1 M −∑ i 1 = 1 0 0 1 2 -3 -2 -1 -4 1 . 2 0 . 8 0 . 6 0 . 4 0 . 2 -0 . 2 -0 . 4 ki M I(f) e π j 2 A m p li tu d e 3 F re q u e n c y Fig.3. FFT filter frequency response and coefficients in the frequency domain The filter coefficients are multiplied by , which corresponds to a shift in frequency by of the frequency response. When all the FFT outputs are considered, a bank of M filters Mk / is obtained, as shown in Fig.4, in which the unit on the frequency axis is M/1 , the sub-carrier spacing. The orthogonality condition appears through the zero crossings: at the frequencies which are integer multiples of M/1 Fig.4. The FFT filter bank (frequency unit: sub-carrier spacing) An FIR filter can be defined by coefficients in the time domain or by coefficients in the frequency domain. The two sets of coefficients are equivalent and related by the discrete Fourier transform (DFT). Returning to the first filter in the bank, the DFT of its impulse response consists of a single pulse, as shown in Fig.3. In fact, the frequency coefficients are , only one filter frequency response is non-zero. 10 12 Frequency Amplitude -0.2 0.2 0.4 1 0.8 0.6 0 2 4 6 8 0 6

PHYDYAS 06/2010 7 f I f ) ( ) ( I , which, according to the sampling theory, is the samples of the frequency response derived from them through the interpolation formula. In the terminology of filter banks, the first filter in the bank, the filter associated with the zero frequency carrier, is called the prototype filter, because the other filters are deduced from it through frequency shifts. It is clearly apparent in Fig.4 that is the frequency response of a prototype filter with limited performance, particularly out-of-band attenuation. In order to reduce the out-of-band ripples, it is necessary to increase the number of coefficients in the time domain and, equivalently, in the frequency domain. Then, in the time domain, the filter impulse response length exceeds the multicarrier symbol period T . In the frequency domain, additional coefficients are inserted between the existing coefficients, allowing for a better control of the filter frequency response. Prototype filters are characterised by the overlapping factor K, which is the ratio of the filter impulse response duration Θ to the multicarrier symbol period T . The factor K is also the number of multicarrier symbols which overlap in the time domain. Generally, K is an integer number and, in the frequency domain, it is the number of frequency coefficients which are introduced between the FFT filter coefficients. Now, the question is how to design the prototype filter and transmit data in such a manner that no intersymbol interference occurs, in spite of the overlapping. 3. Prototype filter design – Nyquist criterion Digital transmission is based on the Nyquist theory: the impulse response of the transmission filter must cross the zero axis at all the integer multiples of the symbol period. The condition translates in the frequency domain by the symmetry condition about the cut-off frequency, which is half the symbol rate. Then, a straightforward method to design a Nyquist filter is to consider the frequency coefficients and impose the symmetry condition. In transmission systems, the global Nyquist filter is generally split into two parts, a half- Nyquist filter in the transmitter and a half-Nyquist filter in the receiver. Then, the symmetry condition is satisfied by the squares of the frequency coefficients. The frequency coefficients of the half-Nyquist filter obtained for K=2,3 and 4 are given in Table1. K 2 3 4 H0 1 1 1 H1 2/2 0.911438 0.971960 H2 - 0.411438 2/2 H3 - - 0.235147 σ2 (dB) -35 -44 -65 Table 1. 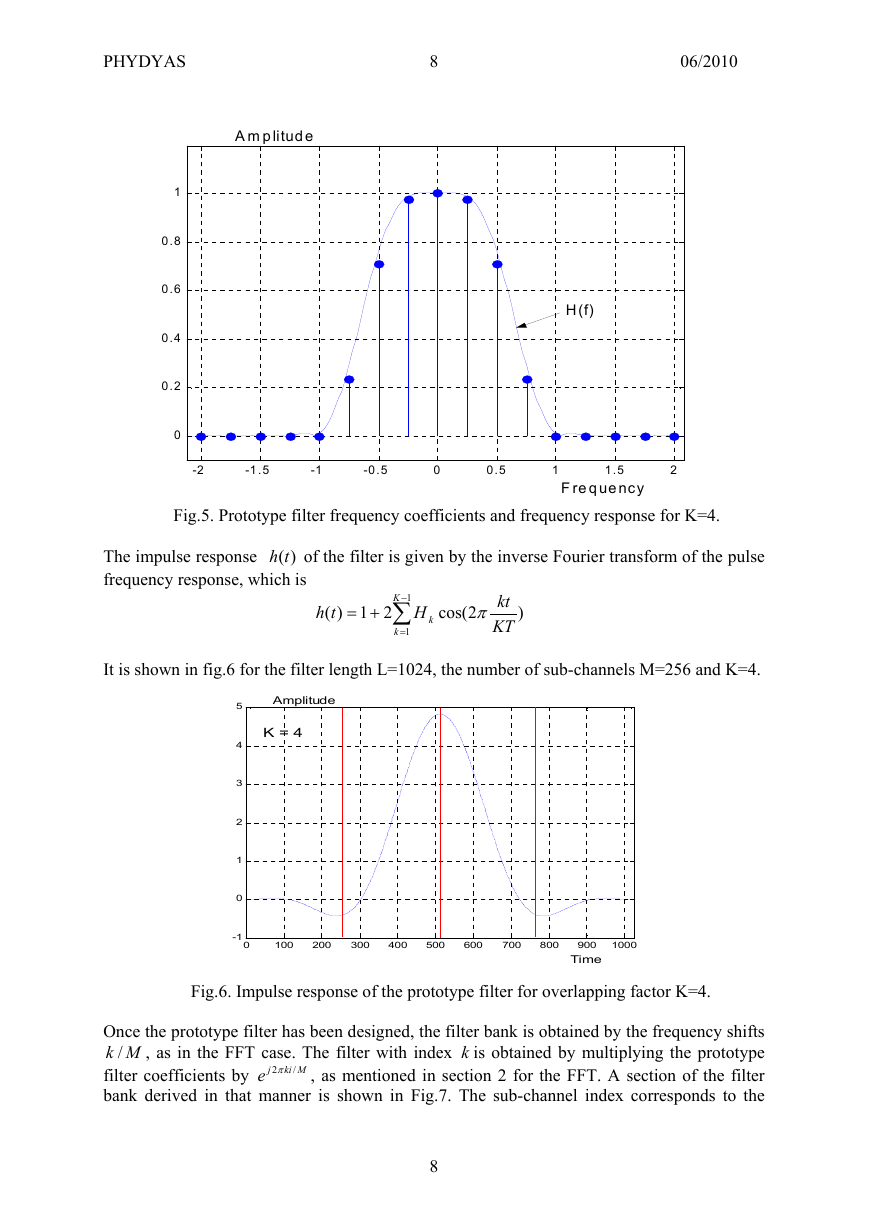Frequency domain prototype filter coefficients In the frequency domain, the filter response consists of 2K-1 pulses, as shown in Fig.5 for K=4. The continuous frequency response, also shown in Fig.5, is obtained from the frequency coefficients through the interpolation formula for sampled signals which yields fH ( ) 1 K = ∑− k −= ( K H )1 − sin( ( π f − k MK sin( ( π k MK f − ) )) ) MK k MK The out-of-band ripples have nearly disappeared and a highly selective filter has been obtained. 7

PHYDYAS 06/2010 8 1 0.8 0.6 0.4 A m p litud e Fig.5. Prototype filter frequency coefficients and frequency response for K=4. The impulse response frequency response, which is th 21)( F re q ue ncy cos( += H (f) )(th 2 π -0.5 -1.5 0.2 0.5 1.5 H -2 -1 ) 0 1 2 0 1 K ∑− k of the filter is given by the inverse Fourier transform of the pulse kt KT k 1 = 5 4 3 2 K = 4 Amplitude It is shown in fig.6 for the filter length L=1024, the number of sub-channels M=256 and K=4. Fig.6. Impulse response of the prototype filter for overlapping factor K=4. Once the prototype filter has been designed, the filter bank is obtained by the frequency shifts /k M , as in the FFT case. The filter with index k is obtained by multiplying the prototype filter coefficients by , as mentioned in section 2 for the FFT. A section of the filter bank derived in that manner is shown in Fig.7. The sub-channel index corresponds to the 900 Time e π j 2 ki M 1000 500 600 800 100 200 300 400 700 -1 1 0 0 / 8

资料库

5GFBMC调制模式介绍文档.pdf

相关推荐

行业

热门标签

最新资料