IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 3, MARCH 2009
997
Density Evolution for Nonbinary LDPC Codes Under
Gaussian Approximation
Ge Li, Ivan J. Fair, Member, IEEE, and Witold A. Krzymien´, Senior Member, IEEE
Abstract—This paper extends the work on density evolution
for binary low-density parity-check (LDPC) codes with Gaussian
approximation to LDPC codes over GF (q). We first generalize the
definition of channel symmetry for nonbinary inputs to include
q-ary phase-shift keying (PSK) modulated channels for prime q
and binary-modulated channels for q that is a power of 2. For
the well-defined q-ary-input symmetric-output channel, we prove
that under the Gaussian assumption, the density distribution for
messages undergoing decoding is fully characterized by (q � 1)
quantities. Assuming uniform edge weights, we further show that
the density of messages computed by the check node decoder
(CND) is fully defined by a single number. We then present the
approximate density evolution for regular and irregular LDPC
codes, and show that the (q � 1)-dimensional integration involved
can be simplified using a dimensionality reduction algorithm for
the important case of q = 2p. Through application of approximate
density evolution and linear programming, we optimize the degree
distribution of LDPC codes over GF(3) and GF(4). The optimized
irregular LDPC codes demonstrate performance close to the
Shannon capacity for long codewords. We also design GF(q) codes
for high-order modulation by using the idea of a channel adapter.
We find that codes designed in this fashion outperform those
optimized specifically for the binary additive white Gaussian noise
(AWGN) channel for a short codewords and a spectral efficiency
of 2 bits per channel use (b/cu).
Index Terms—density evolution, Gaussian approximation, low-
density parity-check (LDPC) codes.
I. INTRODUCTION
T HIS paper is motivated by the impressive performance
of irregular low-density parity-check (LDPC) codes over
a wide class of channels [1]–[5]. Irregular LDPC codes are
commonly designed using a numerical technique called density
evolution. Developed by Richardson and Urbanke [1], the
method of density evolution is one of the most powerful tools
known for analyzing the asymptotic performance of an LDPC
Manuscript received February 14, 2007; revised April 24, 2008. Current ver-
sion published February 25, 2009. This work was supported by TRLabs, the
Rohit Sharma Professorship, and the Natural Sciences and Engineering Re-
search Council (NSERC) of Canada. The material in this paper was presented in
part at the IEEE International Symposium on Information Theory, Yokohama,
Japan, June 2003.
G. Li was with the Department of Electrical and Computer Engineering/TR-
Labs, University of Alberta, Edmonton AB T6G 2V4 , Canada. She is now with
JP Morgan Securities Inc., New York, NY 10017 USA (e-mail: geli@ece.ual-
berta.ca).
I. J. Fair and W. A. Krzymien´ are with the Department of Electrical and Com-
puter Engineering/TRLabs, University of Alberta, Edmonton, AB T6G 2V4,
Canada (e-mail: fair@ece.ualberta.ca; wak@ece.ualberta.ca).
Communicated by H.-A. Loeliger, Associate Editor for Coding Techniques.
Color versions of Figures 2, 4–6, 8, and 9 in this paper are available online at
http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TIT.2008.2011435
code ensemble specified by a degree distribution pair. With the
symmetry of the channel and decoding algorithm as one of its
fundamental assumptions, this method can be applied to a wide
class of binary-input symmetric-output channels,
including
the binary erasure channel (BEC), binary symmetric channel
(BSC), and additive white Gaussian noise (AWGN) channel, as
well as to various iterative decoding algorithms that fall into the
category of message passing algorithms. The density involved
in this numerical technique is the probability density function
(pdf) of the messages passed at each decoding iteration. Under
a tree-like assumption, density evolution computes the exact
density of messages as they evolve from iteration to iteration,
and can be used to evaluate the asymptotic bit-error probability
of the code ensemble for each iteration. Allowing for infinite
iterations, it can be used to determine the decoding threshold,
which is the boundary of the error-free region for the asymp-
totic performance of the code ensemble when the code length
tends to infinity. Based on the performance concentration the-
orem and cycle-free convergence theorem presented in [1], the
threshold value can be understood as the bound on achievable
performance of an actual LDPC code with a sufficiently large
block length after a sufficient number of iterations. The design
of a good LDPC code for a certain channel is accomplished by
searching for a near-optimum degree distribution pair with the
largest threshold [1]. Using density evolution and linear search
techniques, Richardson et al. designed irregular LDPC codes
capable of very closely approaching the Shannon limit at very
large block lengths [1], [6]. For example, a carefully designed
rate-
bits
(
at just 0.0045 dB away from the Shannon limit in the AWGN
channel [6].
information bits) exhibits a bit-error rate (BER) of
irregular LDPC code with a block length of
Full density evolution for AWGN channels is computation-
ally intensive. Chung et al. [2] proposed a simplified version
to estimate the threshold with sum–product decoding of binary
LDPC codes over AWGN. Their idea is to approximate the
density of messages (expressed as log-likelihood ratio (LLR)
values) by a Gaussian distribution. Using the symmetry property
of the messages [1], the variance of Gaussianly distributed mes-
sages is found to be equal to twice the mean [1]. The problem
of calculating the message distribution over a one-dimensional
(1-D) real space then collapses to the problem of updating a
single number, i.e., the mean of the messages.
Although binary LDPC codes are known to be powerful
enough to achieve channel capacity, it is nevertheless worth
exploring the potential of nonbinary codes, especially for
channels with input from high-order constellations, which in
principle support higher capacity than those employing binary
0018-9448/$25.00 © 2009 IEEE
�
998
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 3, MARCH 2009
phase-shift keying (BPSK) signaling. Several possible ap-
proaches for using nonbinary alphabets with LDPC codes have
been proposed in the literature. In [7], Gallager used modulo-
arithmetic for his
-ary codes. In [8], Davey and Mackay
introduced LDPC codes using finite field arithmetic, and they
-ary symbol
focused mainly on the case of transmitting a
bits. Nonbinary LDPC codes were also
as a binary string of
considered by Sridhara and Fuja in [9]. They designed codes
over certain rings and groups and mapped them onto phase-shift
keying (PSK) signal sets to yield geometrically uniform signal
space codes.
As pointed out by Richardson et al. [1], full density evolution
can be applied to LDPC codes over large alphabets but the cal-
culation of the message pdf, which is defined over a multidimen-
sional real space, becomes intractable for alphabet sizes larger
than . Instead, Davey and Mackay [8], [10] evaluated their non-
binary codes using Monte Carlo simulation and conducted com-
puter searches for good LDPC codes by minimizing some non-
linear cost functions such as the required average number of de-
coding iterations or the average entropy of a -ary code symbol
for each decoding iteration. Similarly, Sridhara and Fuja esti-
mated the entropy of decoding messages by Monte Carlo simu-
lation, and looked for good degree profiles by minimizing the
at which the entropy would drop below
threshold of
) after a certain number of iterations
a small value (e.g.,
(e.g., 50). Instead of doing a costly full iterative decoder simu-
lation, Byers and Takawira [11] simulated separately the two
component decoders of an LDPC decoder: the variable node
decoder (VND) and the check node decoder (CND). They as-
sumed the input/output messages to each decoder are multidi-
mensional Gaussian, and proposed a correlation model to ac-
count for the pairwise correlation among the elements of the
LLR vector at the CND output. Using the extrinsic information
transfer (EXIT) charts to visualize the exchange of mutual infor-
mation between the two decoders, they designed better GF
codes than those of [10]. Similar work regarding the design of
nonbinary LDPC codes using EXIT charts can be found in [12].
Also based on EXIT curves, the work in [13] provided upper
bounds on the thresholds for various nonbinary LDPC ensem-
bles.
A more systematic approach to the design of nonbinary
LDPC codes was taken by Bennatan and Burshtein in [14] for
memoryless channels. They considered nonbinary LDPC codes
for use with high-order modulation in AWGN. This composite
channel of AWGN and high-order modulation is not symmetric
by itself, so they based their analysis on random-coset LDPC
. The use
codes rather than ordinary LDPC codes over GF
of coset codes symmetrizes the memoryless channels, and thus
the decoding messages. They proved that under the Gaussian
approximation and the so-called permutation invariance as-
-dimensional
sumption, the entire distribution of the
messages can be described by a single scalar parameter. They
applied this property to develop EXIT charts for their codes,
codes that perform within 0.56
and designed good coset GF
dB of the unconstrained Shannon limit at a spectral efficiency
of 6 bits per channel use (b/cu).
A particularly interesting family of LDPC codes are the
so-called hybrid codes, defined over not just one field but a
finite set of fields of different orders [15]. These codes were
proposed to capitalize on the advantages of families of both
binary and nonbinary LDPC codes, and the application of such
codes over frequency-selective channels has been studied in
[16]. A hybrid code needs to be handled carefully, through
transformations of truncation and extension, when passing
messages between nodes defined over different fields. Ex-
tending the main results of our work in [17] to the optimization
of hybrid codes, the authors of [16] designed hybrid codes for
low rates and demonstrated their good frame (block) error rate
(FER) results at practical short-to-medium codeword lengths.
In this paper, we focus on LDPC codes defined over GF
,
similar to those suggested in [8]. We extend the application of
density evolution and consider how to evaluate the asymptotic
. We are interested
performance of LDPC codes over GF
in -ary codes not only for the binary modulated channel but
also when they are mapped onto -ary signal sets. To accom-
plish this, we generalize the definition of channel symmetry for
-ary inputs, and prove that when this symmetry condition is
fulfilled, code performance does not depend on the codewords
that are transmitted. For codes over a -ary alphabet, the mes-
-dimensional
sages that are passed during decoding are
vectors representing a probability distribution over the -ary al-
phabet. It is in general difficult to track message densities in the
entire real space. In order to simplify the threshold analysis, we
also consider Gaussian approximation of decoding messages,
similar to that in [6] and [14]. For the well-defined -ary-input
symmetric-output channel, we prove that under the Gaussian
assumption, the density evolution for messages undergoing de-
quantities. Assuming
coding is fully characterized by
uniform edge weights, we further show that the density of the
decoding messages computed from the CND is fully defined by
a single number.
This paper is organized as follows. In Section II, we present
and
a brief introduction of LDPC codes defined over GF
the -ary sum–product algorithm. In Section III, we generalize
the definition of channel symmetry for nonbinary inputs and
prove the property of message symmetry during sum–product
decoding. With the symmetric properties of the channel and
the sum–product algorithm, we show that we can assume the
all-zero codeword for our extended density evolution. In Sec-
tion IV, we test for multivariate normality of decoder messages
and discuss the validity of our Gaussian approximation. We
prove that if the messages are Gaussianly distributed, the co-
variance matrix can be uniquely determined by the mean vector.
Section V contains a brief introduction to the density evolution
for binary codes with Gaussian approximation. The approxi-
mate density evolution for regular and irregular codes, as well
as the optimization algorithm using linear programming, are
then presented in Section VI. Our method of updating the mean
-dimensional integra-
values at check nodes involves a
tion. This computation becomes demanding for
. To sim-
plify this calculation, in Section VII we propose a dimension-
. In
ality reduction algorithm for the important case of
Section VIII, we introduce several examples of symmetric chan-
nels with -ary inputs. We show that for a prime , the AWGN
channel with inputs from the -PSK constellation is symmetric,
, the transmission of
and when
for some positive integer
�
LI et al.: DENSITY EVOLUTION FOR NONBINARY LDPC CODES
999
a
-ary symbol over a binary modulated channel using a group
bits or using a Walsh word of length
is also symmetric.
of
For channels that are not symmetric, but static in the sense that
they do not change over a codeword’s duration, we adopt the
concept of channel adapter and show that the symmetry condi-
tion is fulfilled for the augmented channel regardless of under-
lying modulation and physical channel. For the symmetric chan-
nels introduced in Section VIII, we provide optimized degree se-
quences of nonbinary LDPC codes and discuss their empirical
BER performance over AWGN. We also investigate the effect
for binary AWGN channels by comparing
of field order
the threshold values of rate-
quasi-regular LDPC codes for
. Section IX summarizes this work and suggests pos-
various
sible directions of future work.
II. BACKGROUND OF -ARY SUM–PRODUCT DECODING
In this section, we provide a general description of
-ary
LDPC codes and the -ary sum–product decoding algorithm.
Further details regarding -ary LDPC codes can be found in
[10].
A -ary LDPC code is defined over GF
1 and consists of a
set of codewords satisfying the constraints specified by an
sparse parity-check matrix
such that
(1)
where
GF
GF
.
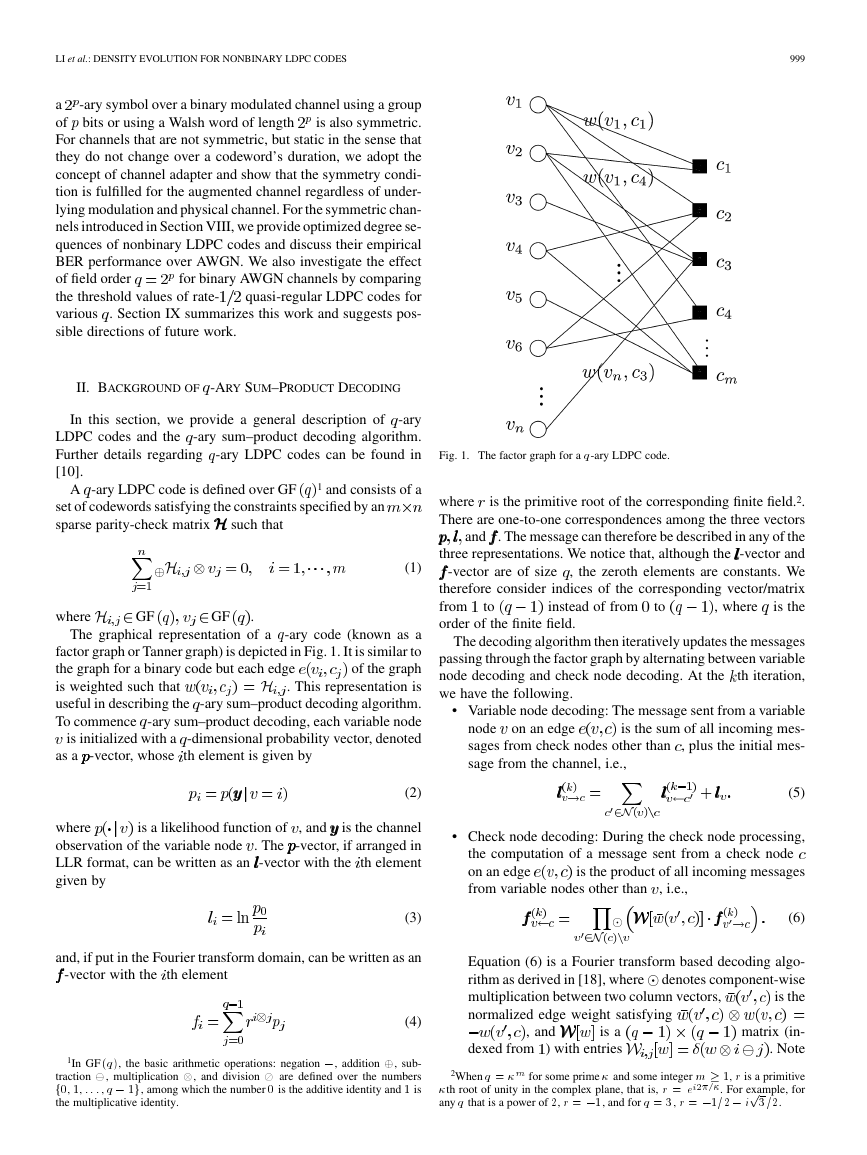
The graphical representation of a
-ary code (known as a
factor graph or Tanner graph) is depicted in Fig. 1. It is similar to
of the graph
the graph for a binary code but each edge
. This representation is
is weighted such that
useful in describing the -ary sum–product decoding algorithm.
To commence -ary sum–product decoding, each variable node
is initialized with a -dimensional probability vector, denoted
as a -vector, whose th element is given by
Fig. 1. The factor graph for a q-ary LDPC code.
where
is the primitive root of the corresponding finite field.2.
There are one-to-one correspondences among the three vectors
and . The message can therefore be described in any of the
three representations. We notice that, although the -vector and
-vector are of size , the zeroth elements are constants. We
therefore consider indices of the corresponding vector/matrix
from to
is the
order of the finite field.
instead of from to
, where
The decoding algorithm then iteratively updates the messages
passing through the factor graph by alternating between variable
node decoding and check node decoding. At the th iteration,
we have the following.
Variable node decoding: The message sent from a variable
is the sum of all incoming mes-
node
sages from check nodes other than , plus the initial mes-
sage from the channel, i.e.,
on an edge
(2)
(5)
is a likelihood function of
is the channel
where
observation of the variable node . The -vector, if arranged in
LLR format, can be written as an -vector with the th element
given by
, and
Check node decoding: During the check node processing,
the computation of a message sent from a check node
on an edge
from variable nodes other than , i.e.,
is the product of all incoming messages
(3)
(6)
and, if put in the Fourier transform domain, can be written as an
-vector with the th element
(4)
1In GF (q), the basic arithmetic operations: negation �, addition �, sub-
traction , multiplication
, and division � are defined over the numbers
f0; 1; . . . ; q � 1g, among which the number 0 is the additive identity and 1 is
the multiplicative identity.
Equation (6) is a Fourier transform based decoding algo-
denotes component-wise
rithm as derived in [18], where
is the
multiplication between two column vectors,
normalized edge weight satisfying
is a
dexed from ) with entries
, and
matrix (in-
. Note
�th root of unity in the complex plane, that is, r = e
2When q = � for some prime � and some integer m � 1; r is a primitive
. For example, for
any q that is a power of 2, r = �1, and for q = 3; r = �1=2 � ip3=2.
�
1000
that
shuffles the components of
edge weight
.
is a permuted identity matrix. Multiplying
by
to take into account the
III. SYMMETRY OF -ARY SUM–PRODUCT DECODING
The decoding analysis in [1] was performed for the binary-
input symmetric-output channel. The defining characteristic of
this channel is that the conditional pdf of the channel output
where
satisfies
given input
.
As an extension, we define a symmetric-output channel whose
. This definition is compat-
inputs are from GF
ible with that of the binary-input symmetric-output channel and
-ary symbols in bi-
includes the special case of transmitting
nary format with uses of an AWGN channel. This -ary input
channel is symmetric in the sense that the channel capacity can
be achieved using equiprobable inputs.
Definition 1: A -ary-input symmetric-output memoryless
channel (symmetric channel, in short) is a discrete-time channel
and whose
whose input symbol
output, denoted as a
assumes values in GF
-dimensional column vector
, satisfies the following condition:
GF
(7)
is a
on the th
where
and zeros
element of the main diagonal
elsewhere, and is the primitive root of the corresponding field.
matrix with
The above definition is consistent with that of the binary-input
symmetric-output channel. When the input is binary, i.e., when
. It is obvious that the
satisfies the symmetric condition defined
and
, we have
channel output
in (7).
The above definition also includes the special case of trans-
uses of an
to
mitting
AWGN channel. For example, we can map a -ary symbol
binary format
-ary symbols in binary format with
by the following rule:
and send the pair of bits over an AWGN channel as two BPSK
, then it
signals. Denoting the received signal as the pair
is straightforward to verify that
satisfies (7)
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 3, MARCH 2009
Theorem 1: Let
be the decoding message (in LLR
format) of a variable node . If the channel is symmetric, then
satisfies the following symmetric condition:
(8)
where
entries
GF
, and
is a
matrix with
.
Proof: The proof follows immediately from Lemmas 4
through 6 in the Appendix.
Theorem 1 frees the behavior of the sum–product decoding
algorithm from the channel input patterns. Therefore, when the
channel symmetry condition is fulfilled, we can prove that the
error probability of sum–product decoding is independent of the
channel input sequence, and we can assume the all-zero code-
word for analyzing the variations of the pdf of LLR messages
during the decoding iterations.
Theorem 2: The error performance of an LDPC code over a
symmetric channel is independent of the transmitted codeword.
Proof: The proof of the theorem is provided in Subsec-
tion C of the Appendix.
IV. PROBABILITY DENSITY UNDER THE GAUSSIAN
ASSUMPTION
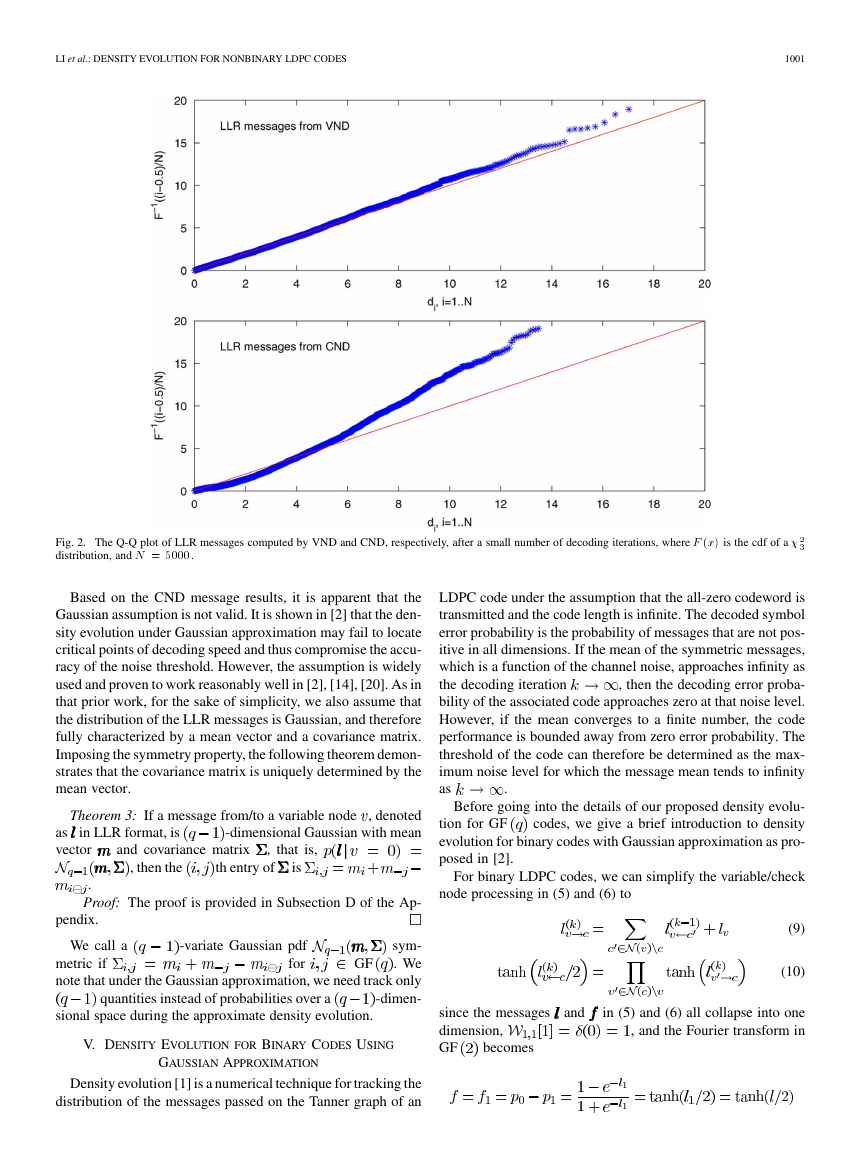
Before we proceed with the Gaussian assumption, we test for
multivariate normality of a -ary LDPC code by examining the
quantile-quantile plot (or Q-Q plot for short) of its empirical
LLR messages.
The Q-Q plot in Fig. 2 was constructed using the theoretical
cumulative distribution function (cdf) of a chi-square distribu-
.
tion with
-dimensional LLR mes-
We collected
for each sample vector
sages and computed a scalar distance
degrees of freedom, that is
samples on the
using the sample mean
and variance–covariance matrix
and it is equal to the sum of the
If
follows the multivariate Gaussian distribution, it can
be transformed approximately into independent standard
conforms
normal distributions so that
to
. In this case, the scalar distance becomes
squared
. By definition, this sum is a chi-square distribu-
. The goodness of fit can hence be assessed
against
[19]. If the theoretical
cdf approximates the observed distribution well, all points in
this plot should fall onto the diagonal line.
elements of
tion and
in the Q-Q plot by comparing the ordered values of
for all
For the above definition of channel symmetry, we prove that
the message being decoded during the sum–product decoding is
symmetric.
Fig. 2 depicts a test run for a regular-
-ary LDPC code
on a binary AWGN channel. The straight lines represent nor-
mally distributed data. As we can see in Fig. 2, for the VND
outputs, most of our points fall on or near the line, which is a
good indicator that our data is normally distributed. However,
the sample messages from the CND depart significantly from
the straight line, which indicates that they are not normally dis-
tributed.
�
LI et al.: DENSITY EVOLUTION FOR NONBINARY LDPC CODES
1001
Fig. 2. The Q-Q plot of LLR messages computed by VND and CND, respectively, after a small number of decoding iterations, where F (x) is the cdf of a �
distribution, and N = 5000.
Based on the CND message results, it is apparent that the
Gaussian assumption is not valid. It is shown in [2] that the den-
sity evolution under Gaussian approximation may fail to locate
critical points of decoding speed and thus compromise the accu-
racy of the noise threshold. However, the assumption is widely
used and proven to work reasonably well in [2], [14], [20]. As in
that prior work, for the sake of simplicity, we also assume that
the distribution of the LLR messages is Gaussian, and therefore
fully characterized by a mean vector and a covariance matrix.
Imposing the symmetry property, the following theorem demon-
strates that the covariance matrix is uniquely determined by the
mean vector.
Theorem 3: If a message from/to a variable node , denoted
-dimensional Gaussian with mean
in LLR format, is
as
vector
and covariance matrix
, that is,
, then the
th entry of
is
.
Proof: The proof is provided in Subsection D of the Ap-
pendix.
We call a
sym-
. We
metric if
note that under the Gaussian approximation, we need track only
-dimen-
-variate Gaussian pdf
for
quantities instead of probabilities over a
GF
sional space during the approximate density evolution.
V. DENSITY EVOLUTION FOR BINARY CODES USING
GAUSSIAN APPROXIMATION
Density evolution [1] is a numerical technique for tracking the
distribution of the messages passed on the Tanner graph of an
LDPC code under the assumption that the all-zero codeword is
transmitted and the code length is infinite. The decoded symbol
error probability is the probability of messages that are not pos-
itive in all dimensions. If the mean of the symmetric messages,
which is a function of the channel noise, approaches infinity as
, then the decoding error proba-
the decoding iteration
bility of the associated code approaches zero at that noise level.
However, if the mean converges to a finite number, the code
performance is bounded away from zero error probability. The
threshold of the code can therefore be determined as the max-
imum noise level for which the message mean tends to infinity
as
.
Before going into the details of our proposed density evolu-
codes, we give a brief introduction to density
tion for GF
evolution for binary codes with Gaussian approximation as pro-
posed in [2].
For binary LDPC codes, we can simplify the variable/check
node processing in (5) and (6) to
(9)
(10)
since the messages
dimension,
GF
becomes
and
in (5) and (6) all collapse into one
, and the Fourier transform in
�
1002
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 3, MARCH 2009
In [2], the message mean at the
th iteration for a reg-
is calculated by taking the expectation of both
ular-
sides of (9) and (10)
Tanner graph where
for all variable nodes
and
for all check nodes .
Assume that during the th iteration, all the messages flowing
to variable nodes through the graph are independent and identi-
, and all the messages to
cally distributed (i.i.d) with mean
. Taking the expectation of
check nodes are i.i.d with mean
both sides of the decoding algorithm in (5) and (6), we obtain
(11)
(12)
where denotes the mean of a random variable (r.v.) , and the
function
is given by
(13)
for a symmetric Gaussian r.v.
. By symmetry of
the linear code, the AWGN channel, and the sum–product algo-
rithm, the all-zero codeword can be assumed to be transmitted
, (11) and
so that
(12) are then used to recursively update the value of
, and
to determine the threshold of the code ensemble as the largest
. With the initialization
for which
Let
as
.
. By (11) and (12) we have
, where
(14)
Since the function
and necessary condition for
is monotonically increasing, a sufficient
is
to go to infinity as
The threshold of the regular-
code ensemble over
AWGN channels is then determined as the largest noise level
for which [2]
(15)
(16)
The density evolution technique can also be applied to irreg-
ular LDPC codes [2]. Using optimization techniques such as
linear programming [1] or differential evolution [3], good de-
gree sequences have been found for irregular codes which at-
tain asymptotically good performance for the family of chan-
nels of interest. Details of the asymptotic analysis of the mes-
sage passing algorithm and density evolution for a variety of
families of channels can be found in [1], [3], [4], [6].
VI. DENSITY EVOLUTION FOR NONBINARY CODES USING
GAUSSIAN APPROXIMATION
Using Gaussian approximation, we now show how to track
the message mean for a nonbinary LDPC code ensemble at the
of the initial message. To
do so, we closely follow the approach taken by Chung et al. in
[2].
th iteration given the mean vector
A. Regular Codes
We first consider regular LDPC codes with nonzero entries
and nonzero
. This corresponds to a regular
within each column of the parity-check matrix
elements within each row of
(17)
(18)
where we use
weights, and we introduce a new function
to represent the set of normalized edge
to denote the expectation of an LLR message
in the
Fourier transform domain
(19)
where is a
Fourier transform domain,
spect to , and the subscript
of the function input.
-dimensional symmetric Gaussian with mean
represents the mapping from to the
stands for expectation with re-
indicates the dimensionality
1) Fixed Edge Weights: In (18), we used
to denote the set
of normalized edge weights. Although not explicitly indicated,
is a function of the weights associated with all the incident
edges to a check node. Suppose we have a check node con-
. The set
necting to
of normalized weights is
with weights
for
, and
, and so on. The sets may or may not be all the same
for
’s. If they differ, we would in
depending on the choice of
general have different mean vectors for messages to different
. In aggregate, the messages to a variable node is a Gaussian
mixture rather than a Gaussian distribution. The mean of the
Gaussian mixture can be obtained by averaging (18) over all
and is given by
(20)
2) Uniform Edge Weight Assumption: Equation (18) sug-
gests that updating the mean of messages to variable nodes is
weight dependent. We can average out the effect of the weights
by assuming that edge weights are selected at random, i.e.,
in (18) can be any value in
assuming that an element of
. By doing so, we obtain
GF
with probability
where
symbolizes the
all-one matrix.
(21)
�
LI et al.: DENSITY EVOLUTION FOR NONBINARY LDPC CODES
1003
for some
. This in turns implies that
Equation (21) reveals that the product on the right-hand side
produces a column vector whose elements are all equal. For this
on the left-hand side must have a
to be true, the parameter
corresponding -vector (in the Fourier transform domain) such
that
itself in the LLR domain is a vector where all elements are equal
and thus can be represented by a single value which multiplies
. This delightful discovery, which
the all-one column vector
follows from the assumption of uniform weights, indicates that
the mean of messages computed by the CND, and thus the den-
sity of these messages, is fully determined by a single number.
This fact will be exploited later on when code optimization is
considered.
Now, we can simplify (21) to
where we define
by
and
by
(22)
It can be shown easily that if
probability of such LDPC code would approach zero.
approaches infinity, the error
Theorem 4: An LDPC code with uniform edge weight
asymptotically achieves error-free performance when the mean
of the LLR decoding message approaches infinity.
Proof: The proof of the theorem is provided in Subsec-
tion E of the Appendix.
has entries of
metric Gaussian is fully described by a single number
the mean vector becomes
variance matrix
It is interesting to note that when a multidimensional sym-
,
and the co-
in the main diagonal and
elsewhere. The Gaussian model is identical to that of the
random-coset LDPC codes in [14] under the assumption of per-
mutation invariance. This is no surprise since the permutation
invariance property in [14] is realized through random permu-
tation of edge weights. However, our result is more general in
that it holds true for ordinary LDPC codes defined on GF
for any physical channel that is symmetric by our Definition 1.
In comparison with the work of [11], our results here verify the
choice of the multidimensional Gaussian model used in [11] for
the CND output messages. The model proposed in [11] based
on observations of empirical LLR messages, captures the rela-
tionship between the mean and correlation matrix for the binary
AWGN channel, and is found to work well with the EXIT tech-
nique for the optimization of GF
codes.
B. Irregular Codes
We have considered Gaussian-approximated density evolu-
tion for regular codes with constant variable degree and check
degree . For irregular codes, variable and check nodes have
disparate degrees. Let
be the maximum variable degree of
be the maximum check
an irregular Tanner graph, and let
and
degree. The graph can be specified by two degree sequences,
rep-
resent the fraction of edges that belong to degree- variable and
check nodes, respectively. Since the number of edges emanating
from variable nodes equals the number of edges incident to
check nodes, the two degree sequences must satisfy the rate con-
straint
, where
and
(23)
after
It is assumed that the individual output of a degree- vari-
able/check node is Gaussianly distributed and, for each such ,
the mean of the distribution is
iterations. Under
this assumption, the messages from the CND in (5), which are a
combination of messages from check nodes of varying degrees,
form a distribution of Gaussian mixture. The same holds for the
messages computed as in (6). Thus, for a uniform weight distri-
bution, we generalize (17) and (22) over the Gaussian mixture
distribution and obtain the following mean updating rule for ir-
regular codes:
(24)
Similar equations can be derived for the case of fixed edge
weights.
C. Code Optimization
and
, these techniques determine a good
The design of good degree sequences
which
give asymptotically good performance for an irregular code has
been extensively addressed in [1], [2], [21]. The optimization
techniques used in [21] and [1] are based on density evolution
and linear programming. Given a desired coding rate and fixed
by minimizing the
probability of erroneous messages subject to a rate constraint.
Chung et al. take a similar approach in [2]. They formulate the
, and seek to max-
optimization problem in terms of
imize the coding rate under a set of linear constraints that ensure
zero error probability after a sufficiently large number of de-
coding iterations. In this work, we adopt the technique outlined
in [2] with minor modifications to account for
-ary codes.
or
As noted earlier in this section, the mean of the output of a
check node depends on the choice of edge weights associated
with this check node. However, the approach considering fixed
parameters and is
edge weights involves the evolution of
very complicated to work with. Instead, we take the assumption
of a uniform distribution of edge weights for code optimization.
For uniform edge weights, we have shown that the mean of the
output of a degree- check node can be specified by a single
number. Therefore, we can express the averaged mean vector of
and denote the vector
CND messages by a single variable
as
. It is straightforward to verify that a
sufficient condition for
to go to infinity as
is [22]
�
1004
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 3, MARCH 2009
where
is defined as
The th element of the -vector, where
explicitly in terms of the LLR message as follows:
, can be written
(25)
and the initial message
Assuming that we are given a variable node degree sequence
, we can thus set up a linear pro-
and search
gramming problem using the constraint
by minimizing the
for a good check node degree sequence
. Note that the objective function
objective function
as shown in (23).
is inversely proportional to the coding rate
Hence, the search solves for a sequence
which defines the
maximum possible coding rate for transmission over the channel
specifying the initial message
.
To assure that iterations always increase the mean of the mes-
sages and that the mean will finally approach infinity after a
as an al-
sufficient number of iterations, we have
is
ternative expression for
defined by
. The function
(26)
with
. Therefore, an alternative approach for
by maximizing the objec-
code optimization is to optimize
.
tive function
,
Since the objective function and the constraint are linear in
the maximization problem can also be solved efficiently using
linear programming.
under the constraint of
Of the two approaches we described here, the latter approach
is used more often because decoding per-
which optimizes
formance of LDPC codes has been found to be more sensitive
to the choice of
than
.
VII. APPROXIMATION OF
FOR
In the previous section, we introduced the function
of
for evaluating the expected value of the Fourier transform func-
tion
jointly Gaussian distributed r.v.’s whose mean
. This evaluation can be done numerically using
is
multidimensional integration techniques, however, a large di-
mensionality indicates high computational complexity. In this
section, we develop an approach to recursively reduce the di-
mensionality of the Fourier transform function for the important
. The proposed dimensionality reduction algo-
case of
rithm is based on Gaussian assumption of composite LLR mes-
sages (defined below). Under this assumption and by exploiting
can be re-
the message symmetry property, we show
defined in (13).
cursively evaluated using the 1-D function
, we note that
that sum to
, we
. Now,
.
reduce by half the size of the alphabet based on GF
let
For an arbitrary nonzero element
disjoint pairs of elements in GF
. Gathering such pairs into a set
be one of the solutions of
there are
GF
GF
for
.
or
or
since
where we define
for
Let denote the column vector of these
values with ar-
bitrary order, and call this vector the composite LLR message
is the logarithm of the ratio
over the alphabet
of the likelihood of a variable node being
and the likeli-
. We show
hood of the variable node being
is
in Theorem 5 below that if the
. If
is also Gaussian,
symmetric, so is the size-reduced vector
then, by Theorem 3, the expectation of
can be computed as a
dimen-
function of
-dimensional
sions. Continuing to do so recursively, the
integration finally reduces to one dimension, for which case the
expectation of the Fourier transform function of a symmetric
in (13) has been well ap-
Gaussian r.v., i.e., the function
proximated using exponential expressions [2].
defined on a real space of
-dimensional vector
Theorem 5: Let and be the LLR vector defined over GF
is symmetric.
is symmetric, then
, respectively. If
and
Proof: The proof is provided in Subsection F of the Ap-
pendix.
It remains to be shown how to evaluate the mean of
given
the mean of . To do this, we have the following theorem.
Theorem 6: Let
of the LLR vector
be the three elements
and
, and let
be the corresponding mean of each variable. If the LLR
for any
and
GF
vector
is symmetric Gaussian as defined in Section IV, then
(27)
where
and
.
Proof: The proof is provided in Subsection G of the Ap-
pendix.
To examine the accuracy of our approximation to
,
we assess thresholds of
-ary quasi-regular LDPC codes on the
binary AWGN channel by using three–dimensional (3-D) nu-
merical integration and by recursively applying (27). By defini-
tion, a quasi-regular LDPC code has nearly uniform variable and
check node degrees [3], and a realization of its parity-check ma-
trix has nearly uniform weights (number of nonzero elements) in
, a quasi-reg-
the columns and rows. For a given coding rate
. We
ular code is fully defined by the mean column weight
compare the difference of the two approaches in Table I for
. We find that for the results in Table I,
0.01 dB, ver-
the approximation errors are in the range of
ifying the accuracy of our dimensionality reduction algorithm
�














 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc