2020年天津商业大学概率论与数理统计考研真题.doc

发布时间：2022-09-21 发布人：admin 分类：说明书资料大小：0.43M 资料格式：doc 举报版权申诉

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

文本预览

2020 年天津商业大学概率论与数理统计考研真题一、单项选择题（每小题 2 分，共 40 分） 1. 若 A 表示事件“掷两枚硬币，结果都是正面向上”，则 A 表示事件（）． A. 掷两枚硬币，结果都是反面向上 B. 掷两枚硬币，结果至少有一枚反面向上 C. 掷两枚硬币，结果至少有一枚正面向上 D. 掷两枚硬币，结果一枚正面向上，一枚反面向上 2. 口袋中有 7 个白球和 3 个黑球，从中任取两个，则取到的两个球颜色相同的概率为（）． A. 0.4 B. 0.6 C. 0.72 D. 0.8 A. 0.2 B. 0.3 C. 0.5 D. 0.8 5. 设二维随机向量(X ,Y) N(0,0,9,16,0.5)，则 D(2X -Y + 1) =（）． A. 8 B. 20 C. 28 D. 52 6. 设随机变量 X 与 Y 相互独立，且都服从[0, 2]上的均匀分布，则 P(max{X ,Y} ≥1) =（）． A. 4 B. 8 C. 12 D. 16

17. 在检验假设中，样本容量一定时，犯第一类错误的概率，犯第二类错误的概率，则（）． 20.以下说法正确的为（）． A. 似然比检验只适用于参数检验 B. 似然比检验只适用于分布的检验 C. 似然比检验既适用于参数检验，也适用于分布的检验 D. 以上说法都不正确二、计算与分析题（共 70 分） 1. （本题 10 分）用甲胎蛋白法普查肝癌，记 C =“被检查者患肝癌”， A =“甲胎蛋白检验结果为阳性”，且由历史资料知，又已知某地居民的肝癌发病率为 P(C) 0.0004． (1) 求某人在一次检测中甲胎蛋白检验结果为阳性的概率; (2) 若某人甲胎蛋白检验结果为阳性，求其患肝癌的概率.（结果保留 5 位小数） 2. （本题 10 分）随机向量(X ,Y) 的联合分布列如下表所示：

请计算： (1) E(X ), E(Y), D(X ), D(Y), E(XY), (X ,Y); (2) P(X + Y ≤1). 三、应用与证明题（每小题 10 分，共 40 分） 2. 一本书共 200 页，每页上的错误数服从参数为 2 的泊松分布，且设每页上的错误数是相互独立的．求这本书的错误数大于 440 个的概率．

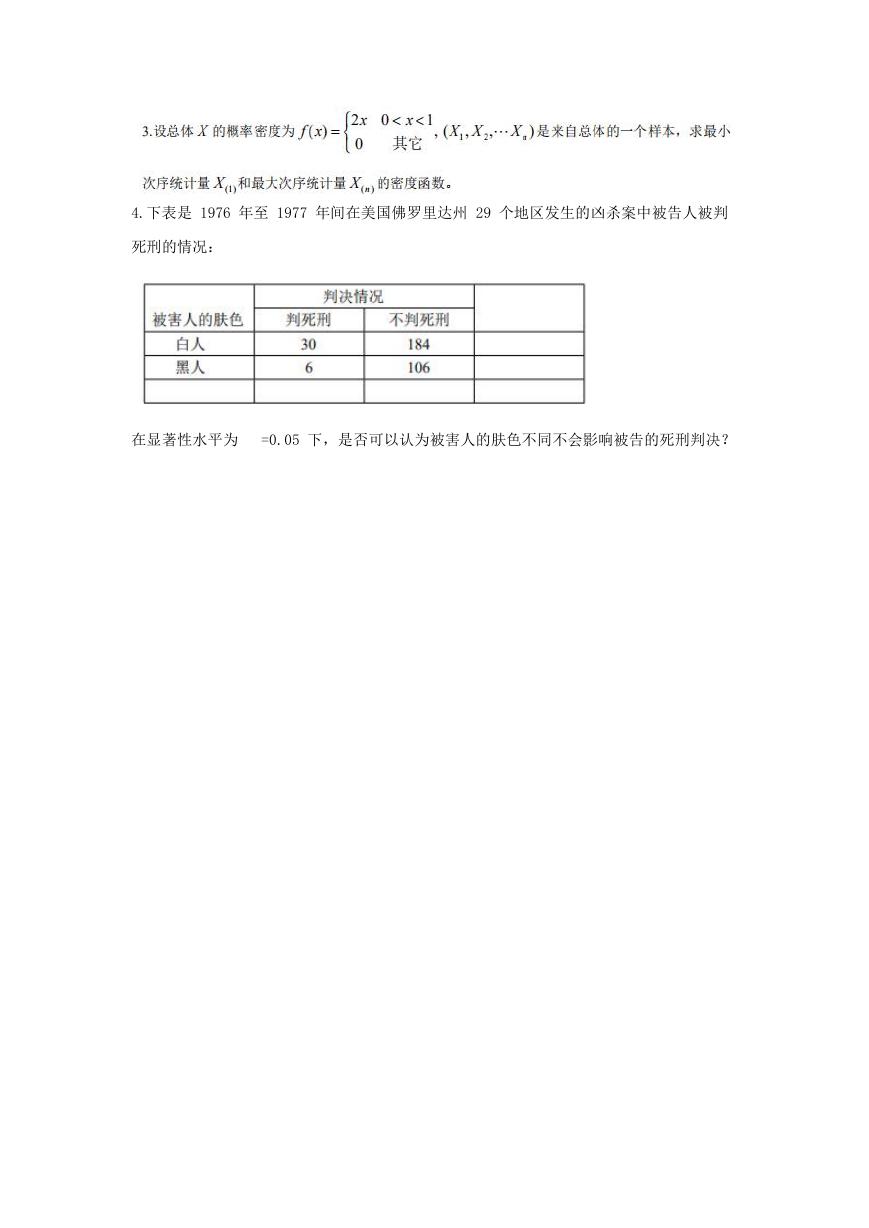
4.下表是 1976 年至 1977 年间在美国佛罗里达州 29 个地区发生的凶杀案中被告人被判死刑的情况：在显著性水平为 =0.05 下，是否可以认为被害人的肤色不同不会影响被告的死刑判决？

分享到：

赞收藏

资料库

2020年天津商业大学概率论与数理统计考研真题.doc

相关推荐

考研

热门标签

最新资料