第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
RLS和LMS自适应算法分析.doc
RLS 和 LMS 自适应算法分析
摘 要 ：本 文 主 要 介 绍 了 自 适 应 滤 波 的 两 种 算 法 ：最 小 均 方 (LMS, Least
Mean Squares) 和 递 推 最 小 二 乘 (RLS, Recursive Least Squares) 两 种 基
本 自 适 应 算 法 。我 们 对 这 两 种 基 本 的 算 法 进 行 了 原 理 介 绍 ，并 进 行 了
Matlab 仿 真 。通 过 仿 真 结 果 ，我 们 对 两 种 自 适 应 算 法 进 行 了 性 能 分 析 ，
并 对 其 进 行 了 比 较 。用 Matlab 求 出 了 LMS 自 适 应 算 法 的 权 系 数 ，及
其 学 习 过 程 曲 线 ， 和 RLS 自 适 应 权 系 数 算 法 的 学 习 过 程 。
关 键 词 ： 自 适 应 滤 波 、 LMS 、 RLS、 Matlab 仿 真
Abstract: this article mainly introduces two kinds of adaptive filtering algorithms: Least
Mean square (LMS), further Mean Squares) and Recursive Least Squares (RLS,
Recursive further Squares) two basic adaptive algorithm. Our algorithms of these two
basic principle is introduced, and Matlab simulation. Through the simulation results,
we have two kinds of adaptive algorithm performance analysis, and carries on the
comparison. Matlab calculate the weight coefficient of the LMS adaptive algorithm, and
its learning curve, and the RLS adaptive weight coefficient algorithm of the learning
process.
Keywords:, LMS and RLS adaptive filter, the Matlab simulation
课 题 简 介 ：零 均 值 、单 位 方 差 的 白 噪 声 通 过 一 个 二 阶 自 回 归 模 型 产
生 的 AR 过 程 。 AR 模 型 的 系 统 函 数 为 ：
H(Z)=
6.11
Z
1
1
8.0
Z
2
假 设 1a =-1.6,
2a =0.8 将 系 统 函 数 转 化 为 差 分 方 程 为 ：
)(
nx
nxa
(
1
)1
na
(
2
)2
)(
nw
其 中 w(n) 为 白 噪 声 ， 参 数 1a =-1.6,
2a =0.8 。 激 励 源 是 白 噪 声 w(n)。
本 文 用 Matlab 仿 真 做 出 了 模 型 系 数 的 收 敛 过 程 及 平 均 的 学 习 曲 线 。
分 别 用 LMS 算 法 和 RLS 算 法 ，分 别 做 出 了 模 型 系 数 的 收 敛 过 程 及 学
1
习 曲 线 ， 还 对 两 种 算 法 的 特 性 进 行 了 对 比 。
引 言 ： 由 于 随 机 信 号 的 未 知 性 和 随 时 间 变 化 的 统 计 特 性 ， 需 要 设 计
参 数 随 时 间 变 化 的 滤 波 器 算 法 ， 即 所谓的自适应滤波。它是利用前一时刻
以获得的滤波器参数的结果，自动的调节现时刻的滤波器参数，以适应信号和噪
声未知的或随时间变化的统计特性，从而实现最优滤波。 自适应滤波器的特性
变化是由自适应算法通过调整滤波器系数来实现的。不 同 的 自 适 应 滤 波 器 算
法 ， 具 有 不 同 的 收 敛 速 度 、 稳 态 失 调 和 算 法 复 杂 度 。
自 适 应 滤 波 算 法 中 利 用 了 输 出 反 馈 ，属 于 闭 环 算 法 。其 优 点 是 能
在 滤 波 器 输 入 变 化 时 保 持 最 佳 的 输 出 ，而 且 还 能 在 某 种 程 度 上 补 偿 滤
波 器 元 件 参 数 的 变 化 和 误 差 以 及 运 算 误 差 。但 其 缺 点 是 存 在 稳 定 性 问
题 以 及 收 敛 速 度 不 高 。所 以 探 讨 如 何 提 高 收 敛 速 度 、增 强 稳 定 性 以 满
足 信 号 处 理 的 高 效 性 、实 时 性 ，一 直 是 人 们 研 究 的 重 点 和 热 点 。本 文
基 对 比 研 究 了 两 类 基 本 的 自 适 应 算 法 LMS 和 RLS ， 并 对 它 们 权 系 数
的 收 敛 过 程 及 学 习 过 程 进 行 了 分 析 。
LMS 原理分析：
LMS 算法是自适应滤波器中常用的一种算法与维纳算法不同的是其系统
的系数随输入序列而改变。维纳算法中截取输入序列自相关函数的一段构造系统
的最佳系数。而 LMS 算法则是对初始化的滤波器系数依据最小均方误差准则进
行不断修正来实现的。因此理论上讲 LMS 算法的性能在同等条件下要优于维纳
算法 但是 LMS 算法是在一个初始化值得基础上进行逐步调整得到的 因此
在系统进入稳定之前有一个调整的时间 这个时间受到算法步长因子的控制
在一定值范围内 增大会减小调整时间 但超过这个值范围时系统不再收敛
的最大取值为 R 的迹。LMS 采用平方误差最小的原则代替均方误差最小的原
则，信号基本关系如下：
2
)(
ny
1
N
0
inxnw
i
()(
)
)(
ne
)(
nd
)(
ny
(
nw
i
)1
写成矩阵形式为：
nw
i
2)(
()(
inxne
)
)(
)(
nXnWny
)(
T
)(
ne
)(
nd
)(
ny
(
nW
)1
nW
2)(
)(
)(
nXne
式 中 W(n) 为 n 时 刻 自 适 应 滤 波 器 的 权 矢 量 ，
)(
nW
[
(
nwnwnw
0
),
),
(
(
2
1
)........
w
(
n
T
)]
N
1
N 为 自 适 应 滤 波 器 的 阶 数 。X(n)为 n 时 刻 自 适 应 滤 波 器 的 参 考 输 入 矢
量 ， 由 最 近 的 N 个 信 号 的 采 样 值 构 成 ，
)(
nX
([
(
nxnx
),
)......
1
(
Nnx
T
)]1
。 d(n)是 期 望 的 输 出 值 ； e(n)为 自 适 应
滤 波 器 的 输 出 误 差 调 节 信 号 ；μ 是 控 制 自 适 应 速 度 与 稳 定 性 的 增 益 常
数 。
3
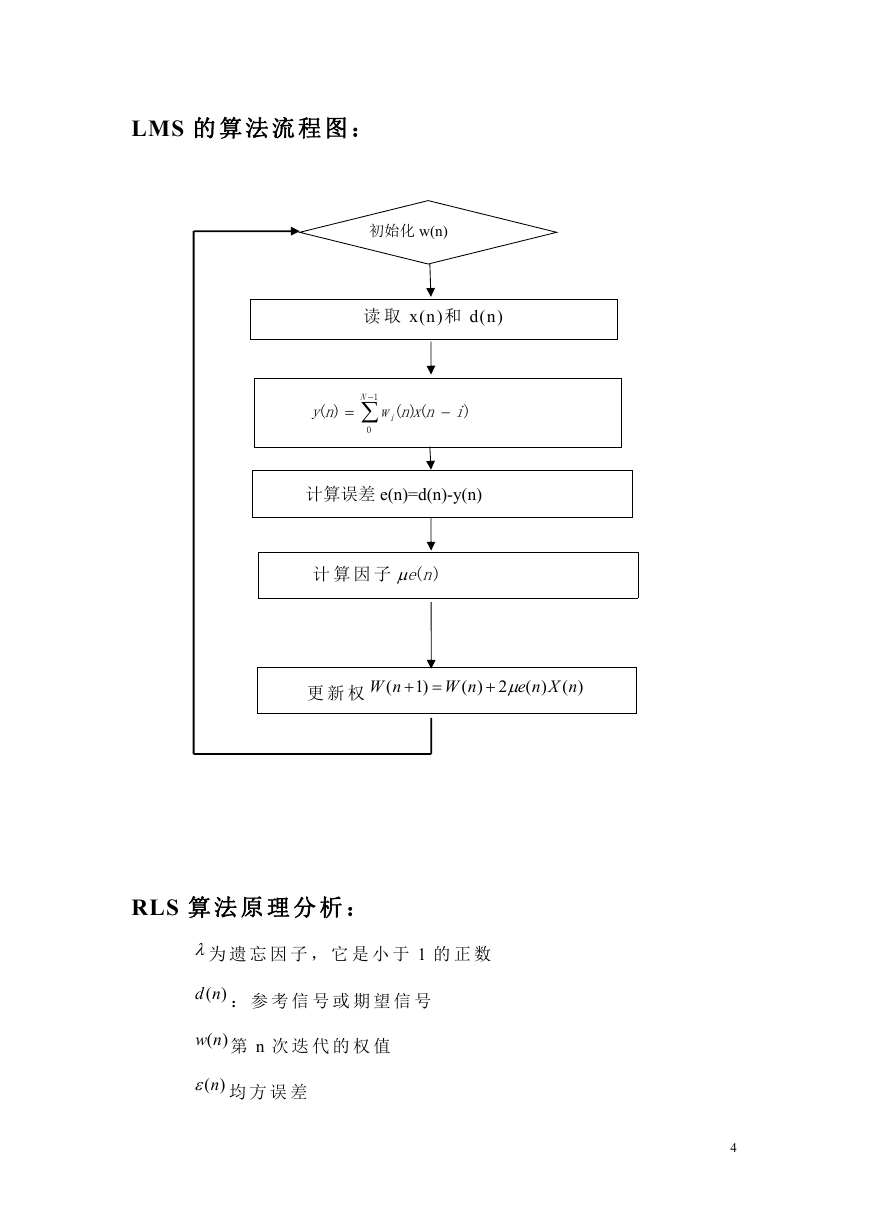
LMS 的 算 法 流 程 图 ：
初始化 w(n)
读 取 x(n)和 d(n)
)(
ny
1
N
0
inxnw
)
()(
i
计算误差 e(n)=d(n)-y(n)
计 算 因 子
)(ne
更 新 权
(
nW
)1
nW
2)(
)(
)(
nXne
RLS 算 法 原 理 分 析 ：
为 遗 忘 因 子 ， 它 是 小 于 1 的 正 数
)(nd ： 参 考 信 号 或 期 望 信 号
)(nw 第 n 次 迭 代 的 权 值
)(n 均 方 误 差
4
按 照 如 下 准 则 ：
)(
n
n
k
0
kn
2
)(
ke
min
越 旧 的 数 据 对 )(n 的 影 响 越 小 。对 滤 波 器 的 系 数 w 求 偏 导 ，并 令 结 果
等 于 0 知
)(
n
w
2
整 理 得 到 标 准 方 程 为 ：
n
k
0
kn
)()(
kxke
0
[
定 义 :
n
k
0
kn
)(
xkx
T
])(
wk
n
k
0
kn
)()(
kxkd
)(
nR
n
k
0
kn
)()(
kxkd
)(
nP
n
k
0
kn
)()(
kxkd
标 准 方 程 可 以 简 化 为 ：
)(
)(
nPwnR
经 求 解 可 以 得 到 迭 代 形 式 ：
(
nR
)1
)(
nR
(
nx
)1
T
(
nx
)1
(
nP
)1
)(
nP
(
nd
()1
nx
)1
定 义 ：
)(
nT
1 nR
)(
， 则 可 知 T 的 迭 代 方 程 为 ：
)(
nT
[
T
1
(
n
)1
(
)(
nxnx
T
)]
1
系 数 的 迭 代 方 程 为
)(
nw
(
nw
)1
()(
nnenk
|
)1
5
其 中 增 益 )(nk 和 误 差
(
nne
|
)1
的 定 义 分 别 为 ：
(
nne
|
)1
)(
(
nwnd
T
)()1
nx
)(
nk
(
nT
T
()(
nTnx
)()1
nx
)()1
nx
参 数 递 推 估 计 ，每 取 得 一 次 新 的 观 测 数 据 后 ，就 在 前 次 估 计 结 果
的 基 础 上 ，利 用 新 引 入 的 观 测 数 据 对 前 次 估 计 的 结 果 ，根 据 递 推 算 法
进 行 修 正 ， 减 少 估 计 误 差 ， 从 而 递 推 地 得 出 新 的 参 数 估 计 值 。 这 样 ，
随 着 新 观 测 数 据 的 逐 次 引 入 ，一 次 接 一 次 地 进 行 参 数 估 计 ，直 到 参 数
估 计 值 达 到 满 意 的 精 确 程 度 为 止 。
6
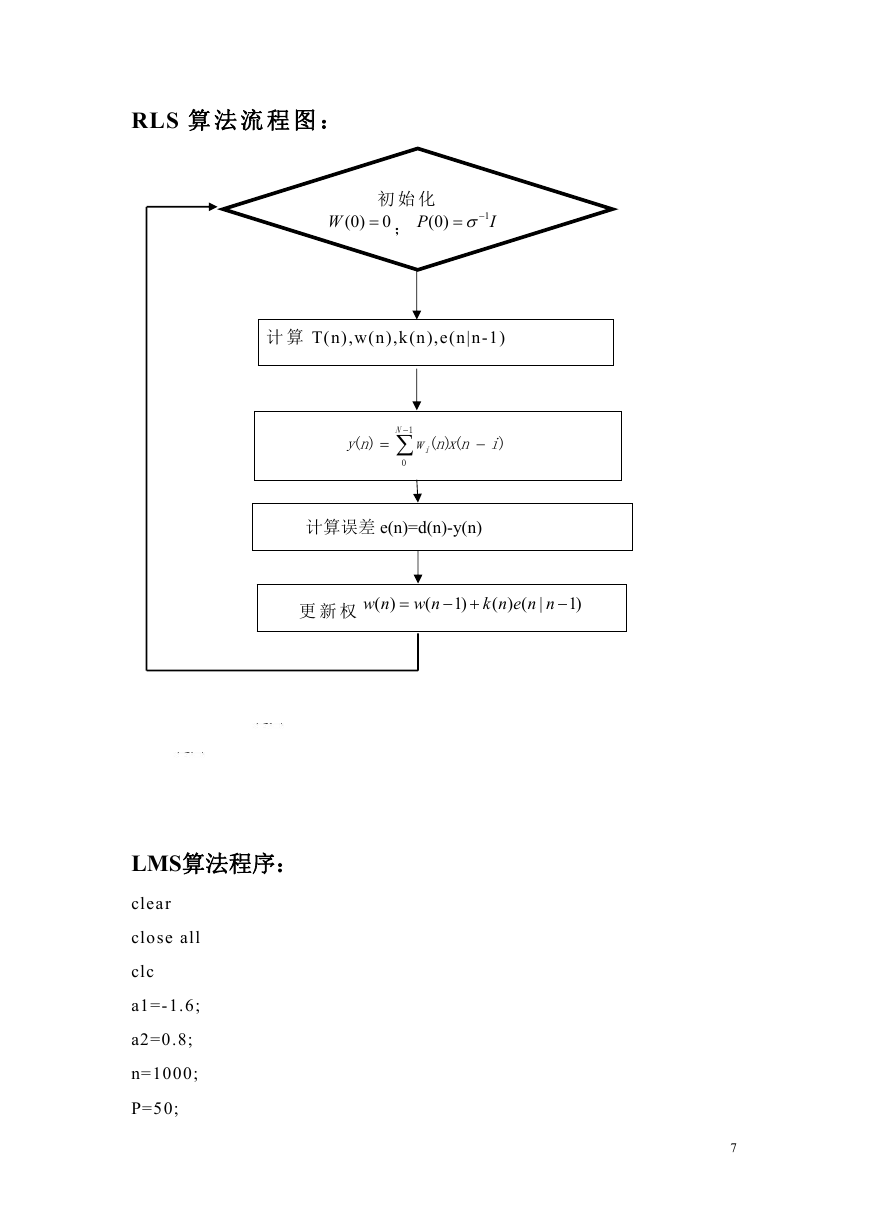
RLS 算 法 流 程 图 ：
初 始 化
W ；
(0) 0
(0)P
1
I
计 算 T(n),w(n),k(n),e(n|n-1)
)(
ny
N
1
0
inxnw
)
()(
i
计算误差 e(n)=d(n)-y(n)
更 新 权
)(
nw
(
nw
)1
()(
nnenk
|
)1
LMS算法程序：
clear
close all
clc
a1=-1.6;
a2=0.8;
n=1000;
P=50;
7
e=zeros(1,n);
ep=zeros(1,n);
ee=zeros(1,n);
x=zeros(1,n)';
w=randn(1,n)';
%算 法
for p=1:P
x(1)=w(1);
x(2)=-a1*x(1)+w(2);
for i=3:n
x(i)=-a1*x(i-1)-a2*x(i-2)+w(i);
end
L=2;
u=0.0005;
wL=zeros(L,n);
for i=(L+1):n
X=x(i-L:1:(i-1));
y(i)=X'*wL(:,i); %i 时 刻 输 出 信 号
e(i)=x(i)-y(i); %i时 刻 误 差 信 号
wL(:,(i+1))=wL(:,i)+2*u*e(i)*X; %i时 刻 滤 波 器 的 权 值
ee(i)=e(i)^2;
end
ep=ep+ee;
end
eq=ep/P;
a1L=-wL(2,1:n);
1到 n个 数
a2L=-wL(1,1:n);
的 1到 n个 数
% a1 在 LMS 算 法 下 值 的 变 化 ，wL 矩 阵 中 第 一 行 的
% a2 在 LMS 算 法 下 值 的 变 化 ， wL 矩 阵 中 第 二 行
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
