MFSK 多进制频率数字调制与解调 1 数字调制的意义： 数字调制是现代通信的重要方法，它与模拟调制相比有许多优点。数字调制具有更好的 抗干扰性能，更强的抗信道损耗，以及更好的安全性；数字传输系统中可以使用差错控制 技术，支持复杂信号条件和处理技术，如信源编码、加密技术以及均衡等。 2 多进制频率数字调制与解调原理： MFSK 简介： 多进制数字频率调制（MFSK）简称多频制，是 2FSK 方式的推广。它是用不同的载波 频率代表种数字信息。多进制频键控（MFSK）的基本原理和 2FSK 是相同的，其调制可以 用频率键控法（频率选择法）和模拟的调频法来实现，不同之处在于使用键控法时其供选 的频率有 M 个，选择逻辑电路也比较复杂。 MFSK 的主要缺点是信号频带宽，频带利用率低。因此，MFSK 多用于调制速率低及多 径延时比较严重的信道，如无线短波信道。 2.1 多进制数字频率调制的原理 串/并变换器和逻辑电路 1 将一组组输入的二进制码（每 k 个码元为一组）对应地转换 成有 M 种状态的一个个多进制码。这 M 个状态分别对应 M 个不同的载波频率。当 某 组 k 位二进制码到来时，逻辑电路 1 的输出一方面接通某个门电路，让相应的载频发送出去， 另一方面同时关闭其余所有的门电路。于是当一组组二进制码元输入时，经相加器组合输 出的便是一个 M 进制调频波形。 2.2 多进制数字频率解调的原理 MFSK 的解调同样有相干解调、非相干解调和锁相环法解调等多种解调方式，其中非相 干解调的原理如下图所示 M 频制的解调部分由 M 个带通滤波器、包络检波器及一个抽样判 决器、逻辑电路 2 组成。各带通滤波器的中心频率分别对应发送端各个载频。因而，当某 一已调载频信号到来时，在任一码元持续时间内，只有与发送端频率相应的一个带通滤波 器能收到信号，其它带通滤波器只有噪声通过。抽样判决器的任务是比较所有包络检波器 输出的电压，并选出最大者作为输出，这个输出是一位与发端载频相应的 M 进制数。逻辑 电路 2 把这个 M 进制数译成 k 位二进制并行码，并进一步做并/串变换恢复二进制信息输出， 从而完成数字信号的传输。 

3 设计实验： 在本次设计中，我采用 M=8，也就是 8 进制 FSK 调制，对应的是 3 位二进制组。因为是软件仿真，所 %采样频率 %码元速率 以省去了串并转换的步骤，并且为了观察出不同的频率，所以手动生成信源信号（从 0：M-1）。 clear ; clc ; M=8 ; freq_sep = 200 ; %连续频率间隔（步长） Fs = 40000 ; nsamp = 200 ; x=[0,1,2,3,4,5,6,7,1,6,2,3,5,4,7] %为了观察，手动生成的序列 %因为原函数观察不直观（为双边带），稍加修改了一下，fskmednew 为修改后的函数 y = fskmodnew(x,M,freq_sep,nsamp,Fs,'cont','bin') ; figure(1) subplot(211); stem(x); title('输入信源序列') axis tight %使坐标轴紧凑 subplot(212); plot(real(y)); title(‘多进制频率调制后的信号’) 

%求出调制后的信号长度 %对调制信号做 FFT 对调制后的信号做 FFT 变换，并观察其频谱 N=length(y); y1=fft(y,N); t=-Fs/2:Fs/N:Fs/2-Fs/N; %坐标横轴 figure(2) plot(t,fftshift(y1)); title('频谱图') axis([0,1800,0,500]); %将零频分量移动到数组中心 从图中可以清楚的看出频率分量 200、400、600、800、1000、1200、1400、1600，当然也存在其 它的分量，这是由于 MFSK 不同频率衔接处产生的。 对调制后的信号加入高斯白噪声 figure(3); SNRpBit=60; %信噪比 SNR=SNRpBit/log2(M); y2=awgn(y,SNR-10*log10(0.5)-10*log10(N),'measured',[],'dB'); plot(real(y2)); title('加入高斯白噪声后的已调信号') 

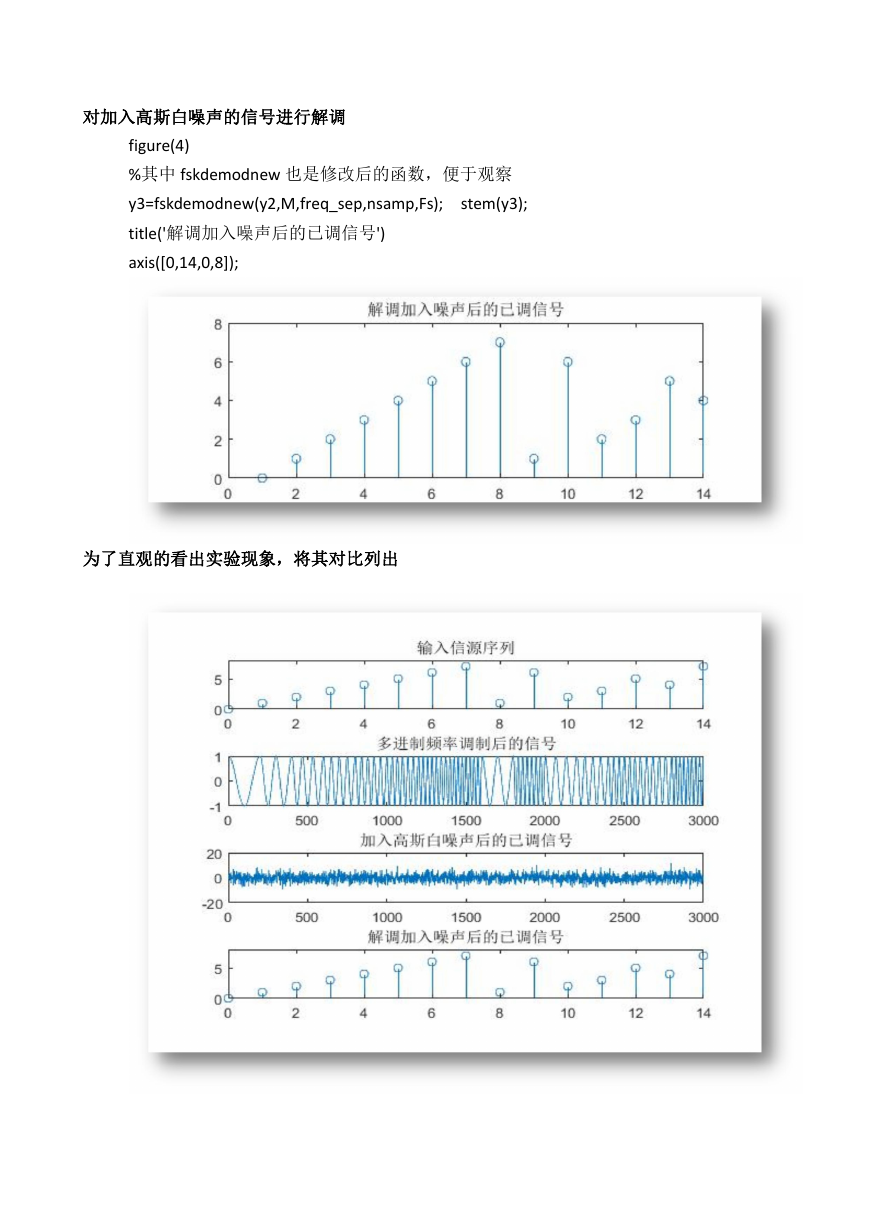
对加入高斯白噪声的信号进行解调 figure(4) %其中 fskdemodnew 也是修改后的函数，便于观察 y3=fskdemodnew(y2,M,freq_sep,nsamp,Fs); title('解调加入噪声后的已调信号') axis([0,14,0,8]); stem(y3); 为了直观的看出实验现象，将其对比列出 

设计实验总结： 本次设计实验让我从根本上认识了数字调制的方式和方法，也让我感受到了 matlab 的 强大仿真能力，这对于学习来说是很便利的。在利用 matlab 自带的函数 fskmod 的时候， 我发现在输入进制为 2 进制时，绘制波形的时候只有一个频率分量，而在输入禁止为 4 进 制的时候，只有两个频率分量，也就是说被平分了。对于这个现象，是不符合原理的。因 为比如为四进制，原序列为 0、1、2、3，在解调的时候，就有两个频率分量没有对应的数 字。仔细分析了 fskmod 和 fskdemod 函数后，我发现，在产生连续相位时，是以-M-1：2： M-1 的方式来进行，产生的实际是双边带的频率信号，所以我改动了部分代码，使产生的 波形更加直观，也符合原理。同时，也在原码中学习了良好的编程方式。这对于后面的学 习是很有帮助的。在设计完后，我觉得数字调制相对于模拟调制是更加方便的，无论是对 于模拟期间来说，还是原理来说，都还是更加有优势一点，并且由于它的强抗干扰能力， 现在已经成为主流。也对于数字信号的处理更加感兴趣。以后也要多加学习 matlab 的实用， 让抽象学习变得更加轻松。