第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
六自由度IRB2400机器人运动学分析及轨迹规划 .pdf
5
10
15
20
25
30
35
中国科技论文在线
http://www.paper.edu.cn
六自由度 IRB2400 机器人运动学分析及轨
迹规划
陈超，李俊，牛怡珺**
（重庆大学机械工程学院， 重庆 400044）
摘要：以 IRB2400 机器人为研究对象，采用 D-H 坐标变换法建立机器人的坐标连杆系，完
成机器人正运动学和逆运动学分析，在此基础上采用三次多项式和五次多项式对机器人进行
轨迹规划。机器人轨迹规划的仿真通过 ADAMS 软件实现，仿真结果表明，五次多项式得
到的速度和加速度曲线光滑连续、没有突变，作业性能优于三次多项式插值法。
关键词：IRB2400 机器人；运动学分析；轨迹规划；仿真
中图分类号：TP242
Kinematics analysis and trajectory planning of Six-DOF
IRB2400
CHEN Chao, LI Jun, NIU Yijun
(College of Mechanical Engineering, Chongqing University, Chongqing 400044)
Abstract: Taking IRB2400 robot as the research object, the D-H parameter method is used to establish
the coordinate linkage system of the robot, complete positive kinematics and inverse kinematics
analysis of the robot, based on that, the trajectory planning of the robot is carried out with cubic
polynomials and quintic polynomials. The simulation of robot trajectory planning is realized by
software ADAMS, the simulation results show that velocity and acceleration curves obtained by quintic
polynomials are smooth and continuous without mutation, the operation performance is better than the
cubic polynomials.
Key words: IRB2400 robot; kinematics analysis; trajectory planning; simulation
0 引言
近年来，机器人得到了非常迅速的发展，不仅在工业发展中扮演着越来越重要的角色，
而且正迅速的向航天、娱乐、服务等领域渗透。因此，对机器人进行运动学分析和轨迹规划
研究具有非常重要的意义。机器人控制的基础就是运动学分析，通过运动学分析可以得到机
器人相邻两连杆之间的位姿矩阵，以此确定机器人末端执行器的位姿[1]。机器人轨迹规划是
为了找到合适的方法来提高机器人作业过程的稳定性和精度，常用的方法有多项式、样条曲
线、抛物线以及不同曲线相结合的方法[2]。本文以 IRB2400 机器人为研究对象，首先对其进
行运动学分析，然后采用三次多项式和五次多项式插值对机器人轨迹规划进行分析，并运用
ADAMS 软件对三次多项式和五次多项式插值两种轨迹规划方法进行比较。
1 IRB2400 机器人运动学分析
1.1 机器人 D-H 坐标系的建立
IRB2400 机器人是 ABB 公司生产的一款工业机器人，该机器人是仿造人的手臂设计的
作者简介：陈超（1990-），男，硕士研究生，主要研究方向：机器人技术
通信联系人：李俊（1966-），男，副教授、硕导，主要研究方向：机器人技术. E-mail: lijunphd@sina.com
- 1 -
中国科技论文在线
http://www.paper.edu.cn
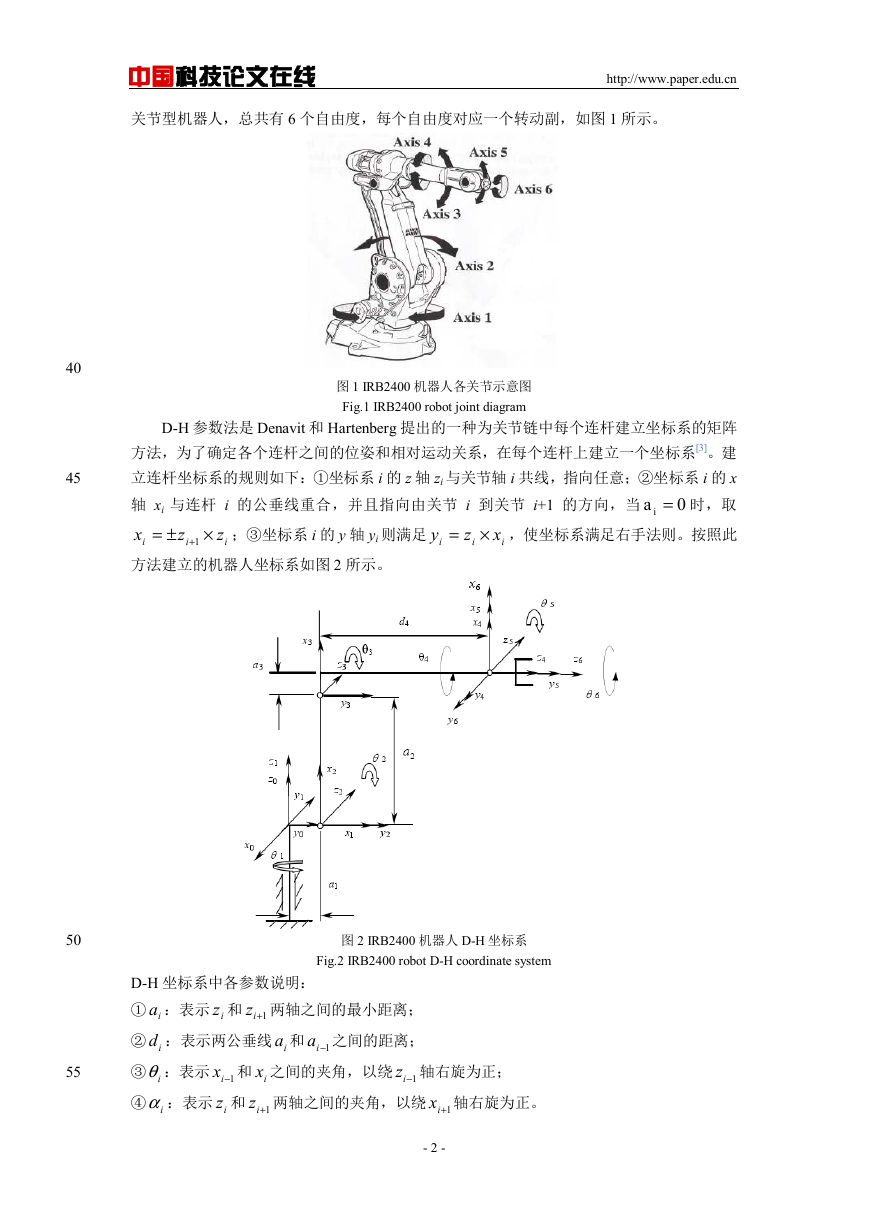
关节型机器人，总共有 6 个自由度，每个自由度对应一个转动副，如图 1 所示。
图 1 IRB2400 机器人各关节示意图
Fig.1 IRB2400 robot joint diagram
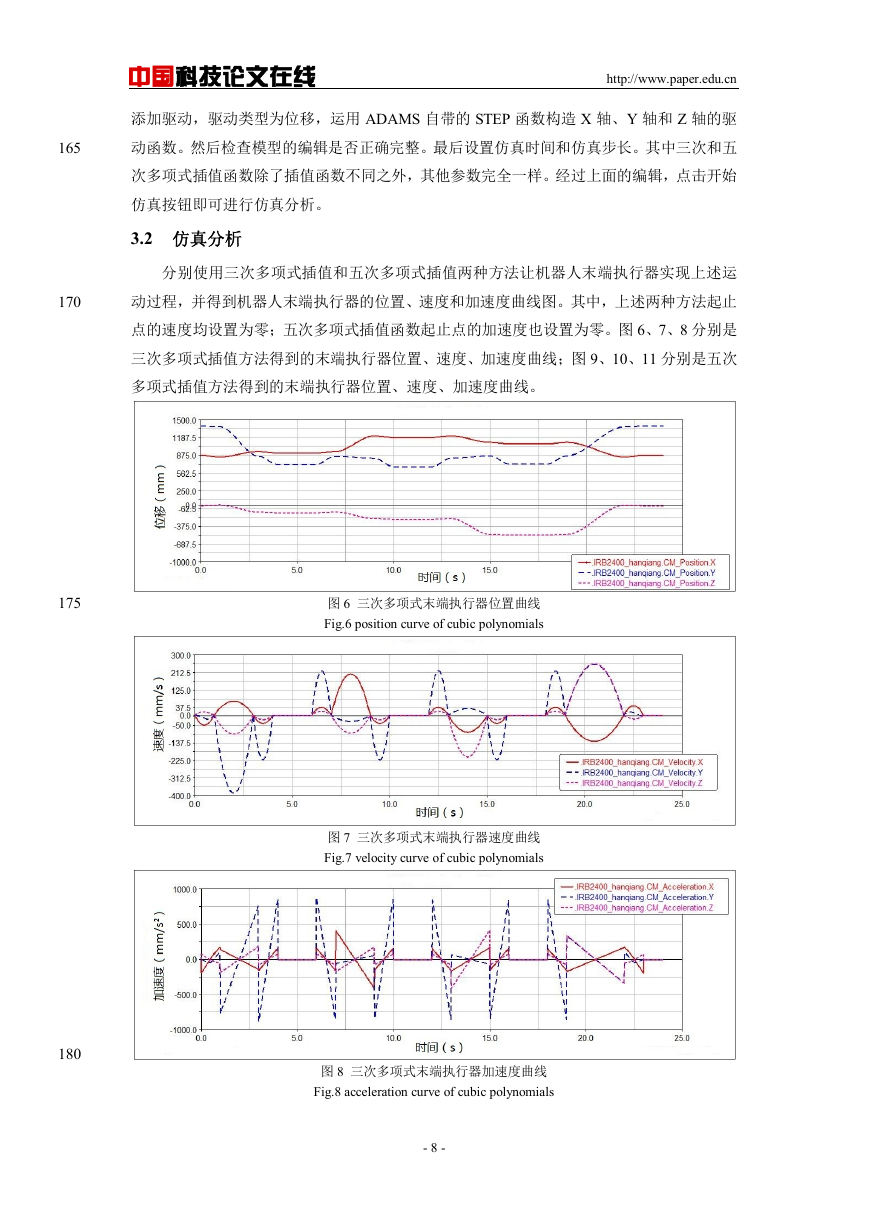
D-H 参数法是 Denavit 和 Hartenberg 提出的一种为关节链中每个连杆建立坐标系的矩阵
方法，为了确定各个连杆之间的位姿和相对运动关系，在每个连杆上建立一个坐标系[3]。建
立连杆坐标系的规则如下：①坐标系 i 的 z 轴 zi 与关节轴 i 共线，指向任意；②坐标系 i 的 x
a i = 时，取
轴 xi 与连杆 i 的公垂线重合，并且指向由关节 i 到关节 i+1 的方向，当
x
，使坐标系满足右手法则。按照此
方法建立的机器人坐标系如图 2 所示。
；③坐标系 i 的 y 轴 yi 则满足
±=
×
x
i
y
i
z
i
z
i
=
0
×
z
+1
i
i
图 2 IRB2400 机器人 D-H 坐标系
Fig.2 IRB2400 robot D-H coordinate system
D-H 坐标系中各参数说明：
① ia ：表示 iz 和 1+iz 两轴之间的最小距离；
② id ：表示两公垂线 ia 和 1−ia 之间的距离；
③ iθ：表示 1−ix 和 ix 之间的夹角，以绕 1−iz 轴右旋为正；
④ iα：表示 iz 和 1+iz 两轴之间的夹角，以绕 1+ix 轴右旋为正。
- 2 -
40
45
50
55
中国科技论文在线
http://www.paper.edu.cn
根据 IRB2400 机器人 D-H 坐标系得到机器人的各个连杆的运动参数和结构参数如表 1
所示：
60
表 1 机器人的连杆参数
Tab.1 Link parameters of IRB2400 robot
连杆序号
1-ia (mm)
1-iα (°)
id (mm)
1
2
3
4
5
6
0
1a
2a
3a
0
0
0
-90°
0
-90°
90°
-90°
0
0
0
4d
0
0
iθ(°)
θ
1
θ
2
θ
3
θ
4
θ
5
θ
6
1.2 机器人运动学正解分析
关节范围(°)
-180°～180°
-100°～110°
-60°～65°
-200°～200°
-120°～120°
-400°～400°
连杆参数
(mm)
=d
4
=a
1
=a
2
=a
3
755
100
705
135
根据第 i 根连杆的 D-H 参数，可以得出齐次坐标变换矩阵 iA ， iA 描述了第 i 根连杆相
对于第 i-1 根连杆坐标系的位姿。现列出所有的齐次坐标变换矩阵：
θ
2
−
−
θ
2
θ
cos
2
0
sin
0
θ
cos
4
0
sin
0
θ
cos
6
0
sin
0
−
−
θ
4
θ
6
−
θ
2
sin
0
cos
0
sin
0
cos
0
sin
0
cos
0
−
−
−
−
θ
4
θ
4
θ
6
θ
6
3
a
0
1
1
0
0
0
0
1
a
0
d
1
4
0
0
1
0
00
01
00
10
=
A
1
65
=
A
3
=
A
5
θ
cos
1
θ
sin
1
0
0
θ
cos
3
θ
sin
3
0
0
θ
cos
5
0
θ
sin
5
0
θ
−
sin
1
θ
cos
1
0
0
θ
−
sin
3
θ
cos
3
0
0
sin
0
θ
cos
5
0
θ
5
−
00
00
01
10
a
0
2
0
0
1
0
0
1
0
0
−
01
0
0
0
1
=
A
2
A
4
A
6
=
=
将以上六个齐次坐标变换矩阵相乘即为机器人末端执行器运动学方程，即机器人末端执
行器相对于固定坐标系的变换可表示为：
=
T
6
AAAAAA
1
6
5
4
3
2
=
x
y
n
n
n
z
0
y
x
o
o
o
z
0
x
y
a
a
a
z
0
x
y
p
p
p
z
1
(1)
70
式中：
nx
ny
[
cc
1
[
cs
1
=
=
23
23
(
ccc
654
(
ccc
654
−
−
ss
64
ss
64
)
−
)
−
css
65
23
css
65
23
]
(
+
ccss
654
1
]
(
−
ccsc
654
1
- 3 -
+
sc
64
+
sc
64
)
)
75
80
85
90
95
23
ss
64
+
+
中国科技论文在线
)
(
−
−
−=
css
nz
s
ccc
65
23
23
654
[
)
(
+
−
=
sss
ox
ss
c
ccc
c
23
65
64
654
1
[
)
(
+
−
=
sss
cs
o y
scc
c
s
23
65
64
654
23
1
(
)
+
+
=
cs
oz
ssc
scc
s
23
23
65
54
654
−=
+
−
sss
cs
sccc
ax
(
)
23
541
1
54
+
+
−=
a y
ssc
cs
sccs
)
(
54
23
1
23
541
=
−
cc
az
scs
54
5
23
23
−
=
ds
acc
px
(
23
23
1
=
−
p y
acs
ds
(
1
3
23
23
−
−=
as
dc
pz
23
23
θcos
=
ic
其中：
i
ac
2
ac
2
as
2
θsin=
i
4
−
is
a
1
a
1
+
+
+
+
ijc
)
)
；
；
23
5
2
4
3
2
4
3
5
2
http://www.paper.edu.cn
]
]
−
+
scss
654
1
ccsc
654
1
(
(
−
−
cc
64
sc
64
)
)
=
cos(
θθ +
i
j
)
；
ijs
=
sin(
θθ +
i
j
)
。
1.3 机器人运动学逆解分析
前面建立了机器人的正运动学方程，在给定机器人各关节的转动角度的情况下，就可以
求出机器人末端执行器的位姿。然而在实际工作中，通常是已知机器人末端执行器的目标位
θ 、 5
θ、
姿，需要求解机器人各关节的角度变化，也就是需要求解各关节变量 1
θ 的值，即求运动学逆解。
6
θ 、 3
θ、 4
θ、 2
运动学逆解问题的解法有封闭解法和数值解法两种。确定了机器人末端执行器的位姿
后，封闭解法通过代数解法和几何解法可得出每个关节变量的数学函数表达式，并且速度快，
效率高，便于实时控制。目前已建立的一种系统化的代数解法为：运用左乘变换矩阵的逆矩
阵来求解机器人末端执行器的运动学逆解，令左右端矩阵对应元素相等，得出可以求解的三
角函数方程式。下面利用代数法求 IRB2400 机器人末端执行器的运动学逆解。
关节变量 1
θ：用逆矩阵 1
1
−A 左乘式（1），把关节变量 1
θ分离出来，然后使左右两边对
θ的值。如下：
应的元素相等就可以求出关节变量 1
θ
sin
1
θ
cos
1
0
0
00
00
01
10
cos
−
sin
0
0
θ
1
θ
1
−
TA
1
1
6
×
=
y
x
n
n
n
z
0
x
y
o
o
o
z
0
x
y
a
a
a
z
0
x
y
p
p
p
z
1
=
T
1
6
(2)
再通过齐次变换矩阵的乘法求出 1
6T 如下：
=
=
c
23
T
1
6
c
23
sss
65
23
4
3
ccc
654
−
ccc
654
AAAAA
2
5
6
−
ss
(
64
−
ccs
654
−
ss
64
0
cs
)
64
−
cc
64
+
ss
)
64
0
令式（2）两端对应的元素相等，可求得：
−
ccc
654
scs
654
−
−
)
sc
64
−
)
csc
23
65
scc
654
−
−
−
s
s
+
23
23
(
(
(
=θ
1
sss
65
23
ssc
65
23
arctan
- 4 -
−
cs
23
5
ca
23
3
−
sd
4
+
ca
22
+
a
1
cc
5
23
−
sa
23
3
−
−
sa
22
−
scc
54
23
ss
54
−
scs
54
23
0
y p
,
p
x
(2
)
。
23
0
cd
4
23
1
100
105
110
115
120
125
中国科技论文在线
θ 、 3
θ、 4
−
pa
,
)
1
−
)
同理可以求出 2
arctan
z
arctan
θ 、 5
θ、 6
θ ：
(
±
2
arctan
,
(
±
2
a
(2
+
−
2
k
k
k
,
p
d
2
3
3
ac
1
y −
as
1
x
,)
2
k
)5
)
4
+
)
6
(
http://www.paper.edu.cn
)2
2
2
a
1
)
−
k
+
(
k
1
−
)2
3
−
k
2
z
2
4
=θ
2
=θ
3
=θ
4
=θ
5
=θ
6
1
da
,
(2
3
4
cs−
(2
,
4
±
k
2
4
cs−
,
2
(2
(
6
arctan
arctan
arctan
arctan
其中：
k
1
=
cp
x
1
+
a
2
1
+
a
sp
y
1
+
p
2
2
z
2
+
=
k
2
k
k
k
3
4
5
−
2
3
a
−
k
1
1
a
2
2
−
sp
z
2
−
as
z
23
−
ac
23
y
−
d
2
4
−
2
ka
11
−
ca
21
−
ca
32
+
ca
32
a
2
−
ca
1
23
+
ca
1
z
23
(
=
cpc
x
2
1
=
acc
x
1
23
−=
acc
23
1
+
sp
)
y
1
+
acs
y
23
1
−
acs
23
1
x
2 机器人末端执行器轨迹规划
机器人在工作过程中的运动轨迹称为机器人轨迹，对机器人末端执行器的位姿变化路
径、速度和加速度进行规划，以满足机器人作业要求称为机器人轨迹规划[4]。机器人轨迹规
划主要包括：多项式、样条曲线、抛物线以及不同曲线相结合的方法。在实际工程中，主要
采用三次多项式对机器人轨迹进行规划，但三次多项式得不到光滑的加速度曲线[5]。针对此
本文将用五次多项式对机器人进行轨迹规划，同时将得到的结果与三次多项式进行对比分
析。
2.1 三次多项式插值
对于三次多项式插值，为了保证机器人系统可以平稳的作业，则各关节的轨迹函数至少
应该满足：起止点有位置约束和速度约束。即满足：
θ =）（
0 θ
0
、
θ
=）（
ft θ
f
•θ
)0( =
、
0
、
=
0
•
ftθ
(
)
下：
（将起止两时刻的速度设为 0）。关节角度、速度、加速度与时间的函数关系如
=θ
t
)(
a
0
+
ta
1
+
2
ta
2
+
ta
3
3
=
•θ
t
)(
••θ
t
)(
a
1
+
2
ta
2
+
2
ta
3
3
=
2
a
2
+
6
ta
3
- 5 -
中国科技论文在线
http://www.paper.edu.cn
据 此 可 以 求 得 多 项 式 各 系 数 ：
0 θ=a
0
，
1 =a
0
，
=
a
2
a
3
−=
(2
θθ −
0
ft
3
f
)
。
2.2 五次多项式插值
(3
ft
2
θθ −
0
f
)
，
130
对于五次多项式插值，其约束条件在三次多项式的基础上增加了起止点加速度约束。即
满足：
θ =）（
0 θ
0
ftθ
(
两时刻的速度设为 0）。关节角度、速度、加速度与时间的函数关系如下：
ft θ
θ
=）（
ftθ
(
、
、
、
、
、
=
)
0
=
0
=
0
f
•θ
)0(
•
••θ
)0(
••
=
0
)
（将起止
135
=θ
t
)(
a
0
+
ta
1
+
2
ta
2
+
3
ta
3
+
4
ta
4
+
ta
5
5
=
•θ
t
a
)(
1
=••θ
2
+
2
ta
2
+
2
ta
3
3
+
3
4
ta
4
+
4
5
ta
5
a
2
+
6
ta
3
+
12
ta
4
2
+
20
ta
5
3
据 此 可 以 求 得 多 项 式 各 系 数 ：
0 θ=a
0
，
1 =a
0
，
2 =a
0
，
a
3
=
)
，
(10
θθ −
f
0
t
3
f
−
=
a
4
(15
θθ −
0
t
f
4
f
)
，
a
5
=
(6
θθ −
0
f
t
5
f
)
。
2.3 轨迹规划
轨迹规划既可以在直角坐标空间进行，也可以在关节空间中进行。在直角坐标空间进行
140
机器人轨迹规划是将末端执行器位姿、速度和加速度表示为时间的函数，根据末端执行器的
信息可以得到机器人相应关节的位置、速度和加速度等参数。在关节空间中进行机器人轨迹
规划是将所有的关节变量表示为时间的函数，机器人末端执行器的运动可以根据关节函数及
其一阶、二阶导数得到[6]。本文在直角坐标空间中进行轨迹规划，其末端执行器的作业轨迹
如图 3 所示。
145
作业路径为：A—B—M—B—C—N—C—D—O—D—A。其中，A 为起始（终止）点，
=
BM
L
CN
+
2
=
L
500
DO
+
2
=
150
mm
，
300
2
(
mm
)
。
500
M 、 N 、 O 为 作 业 点 ， B 、 C 、 D 为 中 间 点 ， 且 有
L
BC
=
L
CD
=
300
mm
，
LAB
=
200
2
+
500
2
(
mm
)
，
LAD
L
=
- 6 -
中国科技论文在线
http://www.paper.edu.cn
150
155
160
图 3 机器人末端执行器轨迹图
Fig.3 Trajectory diagram of robot end actuator
3 机器人数字化建模与仿真分析
3.1 机器人建模与编辑
六自由度 IRB2400 机器人属于主动开式连杆系，各个关节之间没有直接关系，互不干
涉。主要由机座、回转主体、大臂、小臂、腕部等几个部分组成。运用 SolidWorks 建立 IRB2400
机器人的三维模型。首先，建立各个零件的三维模型，包括机座、大臂、小臂、腕部、末端
执行器、电机等。然后，根据机器人的相互配合关系对 IRB2400 机器人进行组装。并将建
立的 IRB2400 机器人模型转换成 Parasolid 格式，为后面导入 ADAMS 软件做准备。机器人
的总装模型如图 4 所示。
将 SolidWorks 中建立的 IRB2400 机器人装配模型导入 ADAMS 软件中，并进行编辑，
首先，设置基本属性，设置重力加速度的数值和方向，各零件的材料和密度等属性。然后，
创建约束，根据机器人的实际工作情况添加约束，创建相应的运动副。初步完成后的机器人
虚拟样机图如图 5 所示。
图 4 IRB2400 机器人装配模型
Fig.4 IRB2400 robot assembly model
图 5 IRB2400 机器人虚拟样机图
Fig.5 IRB240 robot virtual prototype
机器人末端执行器轨迹的设定方法：在 ADAMS 软件中选取机器人末端执行器并为之
- 7 -
165
170
175
180
中国科技论文在线
http://www.paper.edu.cn
添加驱动，驱动类型为位移，运用 ADAMS 自带的 STEP 函数构造 X 轴、Y 轴和 Z 轴的驱
动函数。然后检查模型的编辑是否正确完整。最后设置仿真时间和仿真步长。其中三次和五
次多项式插值函数除了插值函数不同之外，其他参数完全一样。经过上面的编辑，点击开始
仿真按钮即可进行仿真分析。
3.2 仿真分析
分别使用三次多项式插值和五次多项式插值两种方法让机器人末端执行器实现上述运
动过程，并得到机器人末端执行器的位置、速度和加速度曲线图。其中，上述两种方法起止
点的速度均设置为零；五次多项式插值函数起止点的加速度也设置为零。图 6、7、8 分别是
三次多项式插值方法得到的末端执行器位置、速度、加速度曲线；图 9、10、11 分别是五次
多项式插值方法得到的末端执行器位置、速度、加速度曲线。
图 6 三次多项式末端执行器位置曲线
Fig.6 position curve of cubic polynomials
图 7 三次多项式末端执行器速度曲线
Fig.7 velocity curve of cubic polynomials
图 8 三次多项式末端执行器加速度曲线
Fig.8 acceleration curve of cubic polynomials
- 8 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
