第 18 卷第 7 期 系 统 仿 真 学 报© Vol. 18 No. 7 2006 年 7 月 Journal of System Simulation July, 2006 基于 MATLAB/Simulink 机器人鲁棒自适应控制系统仿真研究 （东北大学教育部暨辽宁省流程工业综合自动化重点实验室，沈阳 110004） 高道祥，薛定宇 摘 要：介绍了一种在 MATLAB/Simulink 环境下进行机器人鲁棒自适应控制系统仿真的方法，利 用 Matlab 软件强大的数值运算功能，将系统模型用 Matlab 语言编写成 M-Function（或 S-Function） 文件，通过 User-Defined-Function 模块嵌入到 Simulink 仿真环境中，可以充分发挥 Simulink 模块 实时的动态仿真功能，简化仿真模型的设计，修改和调整。基于 M-Function 建立机器人系统模型 的方法可以推广到其他复杂控制系统的建模，SimMechanics 在建立多自由度连杆机器人受控对象 仿真模型时，简单可靠。 关键词：机器人；Matlab/Simulink；SimMechanics；仿真；鲁棒自适应控制 中图分类号：TP391.9 文献标识码：A 文章编号：1004-731X (2006) 07-2022-04 Simulation Research of Robust Adaptive Control System for Robotic Manipulators Based on MATLAB/Simulink (Key Laboratory of Process Industry Automation, Ministry of Education, Northeast University, Shenyang 110004, China) GAO Dao-xiang, XUE Ding-yü Abstract: A simulation method of robust adaptive control was proposed for the robotic manipulator system. The method took the advantage of the powerful computing function of Matlab to programme M-function (or S-Function) for the system model by Matlab language and embedded it to the Simulink by User-Defined-Function module. The real time dynamic simulating function of Simulink would be exerted adequately and the design, modification and adjust of the system model could be greatly simplified. The method of constructing manipulator control system model based on M-Function could be generalized to the other complicated control system and SimMechanics would make the n-links manipulator model conveniently and credibly. Key words: robotic manipulator; Matlab/Simulink; SimMechanics; simulation; robust adaptive control 另外，由于 SimMechanics 提供了机构的仿真模块集，对于 n 自由度的连杆机器人，也可以采用 SimMechanics 模块进 行组建。 1 n 连杆机器人的仿真模型 如果不考虑摩擦力等外界干扰的作用，机器人的动力学 方程可由下式描述， ),( + τ= qGqqqCqqM )( )( + (1) , , 是 1×n 向量，表示各个关节的位置，速度， qqq 式中， 加速度。 )(qM 是 nn × 阶对称正定的惯量矩阵。 是 1×n 向量，表示离心力和哥氏力项。 )(qG 是 1×n 向量， 表示重力项。τ表示外界输入的控制力矩。由式(1)可以看出， ),( qqqC 引 言 一个新的控制算法在付诸使用之前，无论从经济原因还 是技术角度，都需要经过仿真阶段来测试控制系统的性能和 缺陷。尤其对复杂系统控制的研究，虽然仿真并不能说明控 制算法是绝对合理与可靠的，但随着仿真技术的发展，仿真 的确是系统设计必不可少的中间步骤。 Matlab/Simulink 以其强大的数学运算能力，方便实用的 绘图功能及语言的高度集成性成为系统仿真和自动控制领 域首选的计算机辅助设计工具。Simulink 可以将可视化的模 块 很 方 便 地 组 成 系 统 模 型 的 仿 真 框 图 ， 对 于 使 用 普 通 Simulink 模块不易搭建的复杂控制系统，用 Matlab 语言编 写M-Function 或S-Function 文件，通过User-Defined-Function 模块嵌入到 Simulink 仿真环境中，大大扩充了 Simulink 的 功能。对于机器人这类的复杂控制系统，通过 Simulink 可 以很方便的建立其仿真模型。 机器人控制系统仿真模型中不易采用普通 Simulink 模 块搭建的部分是控制器模型和受控对象—机器人模型，可以 采用 Matlab 语言编写 M-Function 实现控制器和机器人模型。 收稿日期：2005-05-09 修回日期：2005-08-02 作者简介：高道祥（1972-），男，山东蓬莱人，博士生，研究方向为机 器人鲁棒自适应控制。薛定宇（1963-），男，辽宁沈阳人，教授，博导， 研究方向为控制系统 CAD，机器人控制。 • 2022 • 

第 18 卷第 7 期 Vol. 18 No. 7 2006 年 7 月 高道祥，等：基于MATLAB/Simulink 机器人鲁棒自适应控制系统仿真研究 July, 2006 式中，τ表示控制器输出与受控对象输入的关节驱动力矩/ 力， qq, 表示关节的角速度和角位移（在实际系统中这两个 q 表示期望关节轨 向量变量也是很容易测得的）。 d 迹的角加速度，角速度和角位移。 1.1 基于M-Fuction 的机器人仿真模型 , q q , d d 作为被控对象的 n 连杆机器人，虽然其动力学方程非常 复杂，但是其机械结构却非常简单，表现为 n 个杆件组成的 机械系统，每个杆件上只作用一个力矩，这是一般动力学系 统所不具备的特点。据此，可以采用联立约束法[1]对机器人 进行动力学仿真，其基本思想是：应用牛顿力学对每个单独 的杆件进行力学分析，根据描述机构加速度的约束条件建立 起力与加速度之间的关系，由此构成关于构件加速度和约束 力的齐次线性代数方程组，再将方程组写成矩阵形式，就可 以由仿真软件求出每一时刻的力与加速度。文献[4]已经将这 种方法推广到三维的更一般情况。例如，对于一个平面二连 杆机器人，假设机器人末端执行器固接在连杆 2 上，并且含 有有效载荷，其有效载荷可看作连杆 2 顶端的点质量。将其 6 个运动学方程和 8 个动力学方程联立，可以建立一个包含 有 14 个未知变量（连杆转动的角加速度、连杆和有效载荷 在 X 轴，Y 轴方向平动的加速度和连杆关节支座的反力） 的矩阵方程，用 Matlab 语言编写一个函数求解这个矩阵方 程，得到在给定力矩驱动下连杆的角加速度，通过两个积分 器，就可以得到连杆的角速度和角位移，这种方法是不同于 拉格朗日动力学方程的求解方法的，在求解连杆角加速度的 同时，也能够得到末端执行器有效载荷的加速度和各个关节 的受力情况。 , x y y , x , ] = τqqf ), 1 ,( 因此，根据联立约束法，式(3)可以改写成， FFaaq ,[ (4) 式中， q 为连杆角加速度向量，ax，ay 为连杆和末端执行器 有效载荷质心在 X 轴，Y 轴方向平动的加速度，Fx，Fy 为 机器人各个关节在 X 轴，Y 轴方向受到的支反力。可以根 据所研究问题的需要，在 M-Function 函数文件中有选择的 输出式(4)中的向量。 图 1 是一个二连杆机器人的仿真模型，可以采用子模块 封装技术[2]将其封装为单独的一个 Simulink 模块，使整个仿 真框图看上去更清晰，可读性更强。该模型的 M 函数只输 出了关节角加速度 q 。 1 2 1 2 MATLAB Function 1 s 1 s Robot Model Integrator1 Integrator2 图1 基于M-Function的二连杆机器人仿真模型 1.2 基于SimMechanics 的机器人仿真模型 SimMechanics 通 过 一 个 机 构 系 统 模 块 集 拓 展 了 Simulink 在机构仿真中的应用，通过设定机构系统的组件和 特性就能够得到机构的运动学模型。根据下面的步骤，用 SimMechenics 就能够建立一个具有刚体机构特性的 n 连杆 机器人模型： (1) 根据机构模型的结构，用 SimMechanics 模块组下相 应的模块组成系统的结构模型，然后通过各个模块的参数设 置对话框，设置刚体的质量，惯量矩阵和坐标系统。 (2) 设置传感器和驱动器，并对机构进行初始化设置。 (3) 将设计好的控制器的输出力矩传送到驱动器，就能 够进行仿真了。 (4) 在机构的建立和仿真过程中，还可以通过虚拟现实 的可视化工具来观察机构的模型和仿真过程中机构运动的 动画。 另外，在进行连杆机器人的轨迹规划时，一般是根据机 器人的工作任务，先在机器人工作的任务空间，即笛卡尔空 间，规划出一系列符合任务要求的节点，然后面向关节空间， 将这些笛卡尔空间节点转化成相应的关节空间坐标，并用低 次多项式内插这些关节空间节点，然后用得到的期望的关节 轨迹对机器人进行控制。SimMechanics 模块组的驱动器模 块不但可以用力／力矩进行驱动，也可以用关节期望的加速 度，速度和位移来进行驱动，在建立模型的末端执行器上连 接上 Body-Sensor 模块，通过示波器就可以清楚观察机器人 在期望的关节轨迹的驱动下，其末端执行器在笛卡尔空间的 轨迹曲线，这样能够很方便的了解到关节空间的轨迹规划在 理想情况下是否满足笛卡尔空间的任务要求。 图 2 给出了这种方法关于二连杆机器人的 Simulink 仿 真图，同样可以采用子模块封装技术将其封装，这种方法在 建立多自由度连杆机器人或并联机器人的仿真模型时显得 尤为简便可靠。 B F CS1 CS2 B Base Joint1 Initial Condition1 Link1 Initial Condition2 Actuator1 Sensor1 F CS1 CS2 Link2 Joint2 Sensor2 Actuator2 2 1 2 1 图2 基于SimMechanics的二连杆机器人仿真模型 2 机器人鲁棒自适应控制器的仿真模型 机器人的自适应控制利用机器人动力学方程参数线性 化的特点，采用李亚普诺夫原理设计参数辨识律进行参数的 在线估计，适宜用于末端执行器有效载荷大范围变化的场 合。考虑式(1)所示的机器人动力学方程及其参数线性化的特 点[5,6,7]，设计的鲁棒[9]自适应控制律为， • 2023 • 

第 18 卷第 7 期 Vol. 18 No. 7 2006 年 7 月 系 统 仿 真 学 报 July, 2006 ˆ)( qqqqY u , , ,( 1) τ θ = + r r ~Λ− = q q q q q = 式中， ， d r d >nλλ k [ 1 0] [ 1 ，K=diag =diag 回归矩阵，θˆ 为待辩识参数值。 r uKs − + (5) 2 −=~ ~Λ− q q ， >nk ， )(⋅Y 为机器人 0] dqq ，Λ 2 2 1 u u , −= T sY ρ 1 T sY + ~ ~ 1,ρρ 分别为参数辩识误差θ q 式中， ， 2 扰力矩 dτ 的上界, , >εε 1 ρ 1 ~ Λ+= q s ε + 2 ρ 2 s −= ρ 2 ε 1 0 s 2 2 (6) 与外界干 为了防止持续有界干扰的作用使自适应辩识参数发生 漂移，参数估计采用如下的死区自适应算法， ˆ θ ⎧ Γ−= ⎨ 0 ⎩ sY T ||~|| q > ||~|| q ≤ >mγγ ，m 为待辩识参数个数，δ为死 [ 1 0] (7) δ δ 式中，Γ=diag 区大小。 在机器人自适应控制器的仿真设计中，为了更好地利用 Simulink 模块化的仿真功能，将自适应辩识律从控制器中分 离出来，单独组成一个辩识模块，这种自适应控制器的仿真 建模方法同样适用于模糊自适应控制与神经网络自适应控 制。该模块的输入输出关系可用下式表示， qqqqqf ), 2 d ( , , , d d (8) ˆ =θ 那么，自适应控制器模块式可由式(2)改为, )ˆ, θ (9) = τ qf (0 d q , 3 仿真实例 , q d d , qq , 下面是一个关于二连杆机器人自适应控制的仿真。根据 机器人动力学方程式(1)有， = qM )( qqC ,( ) qG )( = 1 cos 2 + + θθθ ⎡ 3 2 ⎢⎣ q cos + θθ 2 2 3 q q sin 2 θ −= ⎡ 23 ⎢⎣ q q θ 13 2 g q g θ ⎡ 4 1 ⎢ g ⎣ sin cos + 2 q 2 − θ 2 + cos θθ 3 θ 2 q q sin 23 0 g cos( ) q 1 ⎤ ⎥⎦ + 2 ， q 2 ⎤ ⎥⎦ ， q 2 ) ⎤ ⎥ ⎦ q cos 1 q cos( 1 θ + 6 q + 2 , , , [ , θθθθθθθ= 3 1 2 5 6 I m r m l θ = + 2 2 1 1 1 1 2 1 rm=θ lm=θ ， 11 12 , 4 + 4 5 为 线 性 化 后 的 参 数 向 量 ， θ = + 2 rm=θ 22 lrm=θ m r 2 122 2 2 。g 为重力加速度。 ， I 3 6 2 ， θ 5 θ 6 ] ， ， 按照式(4)，(8)，(9)编写 M-Function 函数文件嵌入到相 应模块中，由于 Simulink 中连接各个模块的连线能够传递 向量，而且积分模块也能够对向量积分，因此，可将各个模 块组成如图 3 所示的仿真框图进行系统的动态仿真。 机器人机械机构的具体参数设置为，m1=10kg，m2=5kg 为连杆质量， l1 = l2=1m 为连杆长度，r1 =r2=0.5m 为连杆质 心至关节的距离，I1=5/6kgm2，I2=5/12kgm2 为连杆绕质心的 转动惯量，由此可计算出机器人的标称参数值，θ0=[8.33, 1.67, 2.5, 5, 5, 2.5] 。 机 器 人 关 节 空 间 的 期 望 轨 迹 为 q1d=sin(0.67t)+sin(0.3t)rad，q2d=sin(0.39t)+sin(0.5t) rad，机器 q 人关节的初始位置与速度 q10=q20=1rad， rad/s。 10 控制器参数设置为，K=diag(40,40)，Λ=diag(5,5)，ρ1=8， = q = 0 20 ρ2=12， = εε 2 1 = 0.1 。 仿真采用图 1 所示的机器人仿真模型，在仿真过程中， 可以通过程序设定在某个时间改变系统的某个参数或者将 某个参数设定为按某种规律变化的时变参数，也可以在仿真 的中途改动 Matlab 函数中的参数而不用停止仿真，这样能 够立刻观察到改动后的系统运行情况，考察系统在不确定干 扰下的鲁棒性。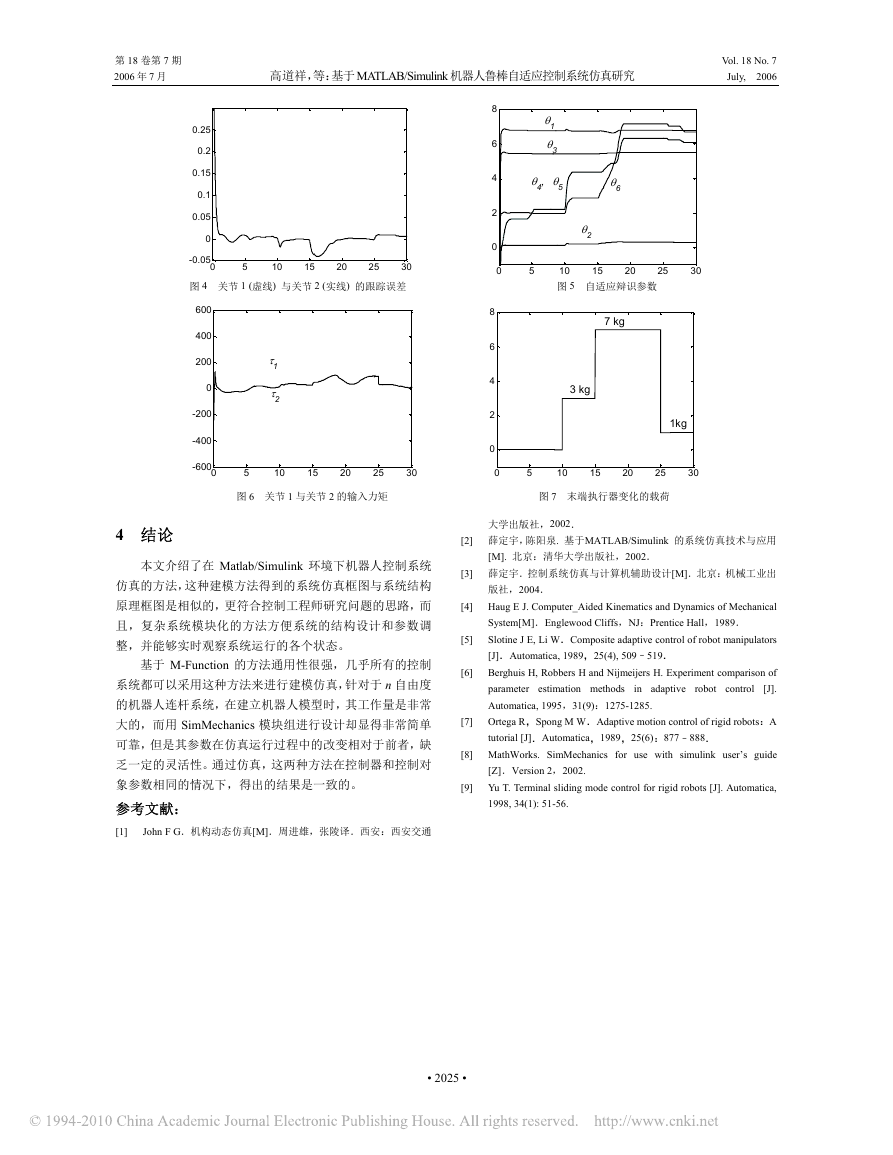 仿真中在机器人末端执行器中加入如图 7 所示变化的 有效载荷，并在输入的控制力矩中混入如下的方波干扰信 号， 1dτ = 8 ⎧ ⎨ 0 ⎩ 0 π t <≤ t <≤ π 2 π ， 2dτ = 5 ⎧ ⎨ 0 ⎩ 0 π t <≤ t <≤ π 2 π 。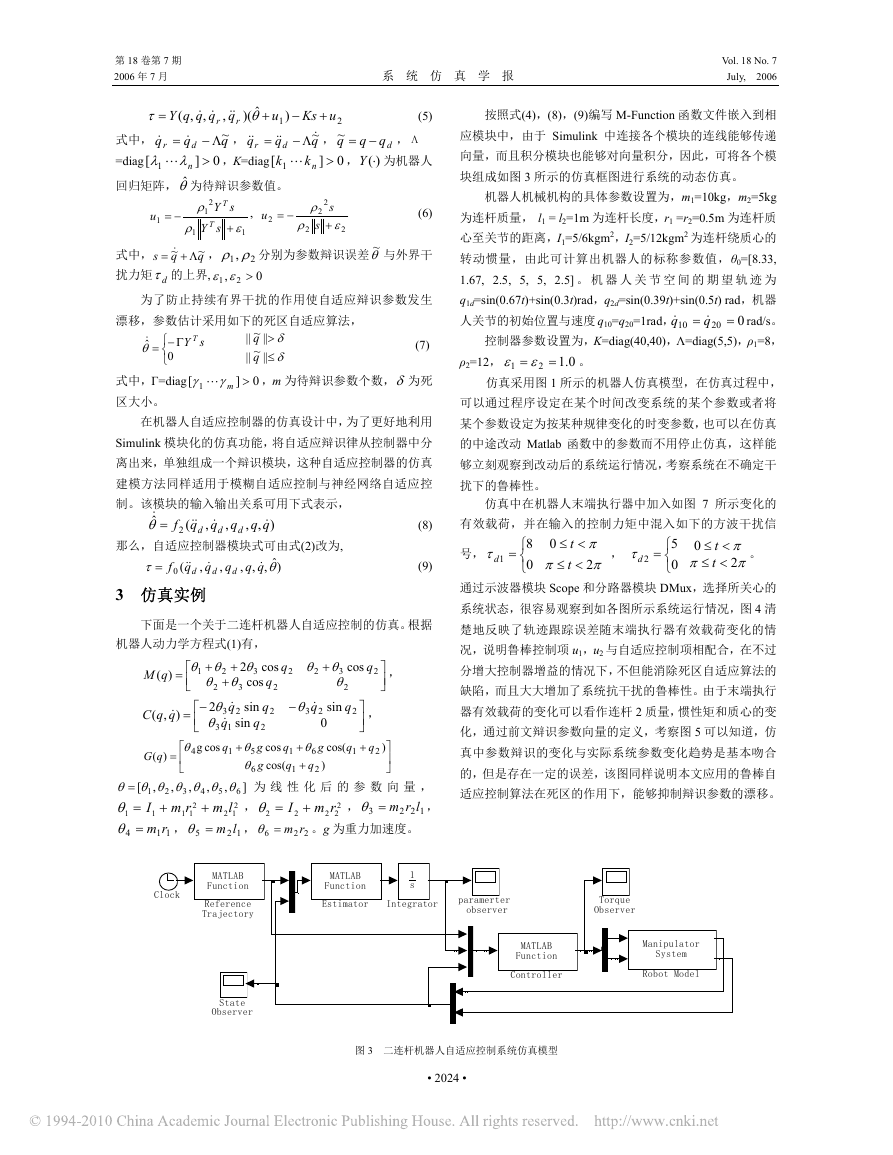 通过示波器模块 Scope 和分路器模块 DMux，选择所关心的 系统状态，很容易观察到如各图所示系统运行情况，图 4 清 楚地反映了轨迹跟踪误差随末端执行器有效载荷变化的情 况，说明鲁棒控制项 u1，u2 与自适应控制项相配合，在不过 分增大控制器增益的情况下，不但能消除死区自适应算法的 缺陷，而且大大增加了系统抗干扰的鲁棒性。由于末端执行 器有效载荷的变化可以看作连杆 2 质量，惯性矩和质心的变 化，通过前文辩识参数向量的定义，考察图 5 可以知道，仿 真中参数辩识的变化与实际系统参数变化趋势是基本吻合 的，但是存在一定的误差，该图同样说明本文应用的鲁棒自 适应控制算法在死区的作用下，能够抑制辩识参数的漂移。 Clock MATLAB Function Reference Trajectory MATLAB Function 1 s Estimator Integrator paramerter observer Torque Observer m Manipulator System Robot Model MATLAB Function Controller State Observer 图 3 二连杆机器人自适应控制系统仿真模型 • 2024 • 

第 18 卷第 7 期 Vol. 18 No. 7 2006 年 7 月 高道祥，等：基于MATLAB/Simulink 机器人鲁棒自适应控制系统仿真研究 July, 2006 0.25 0.2 0.15 0.1 0.05 0 8 6 4 2 0 θ1 θ3 θ4, θ5 θ6 θ2 -0.05 0 5 25 图 4 关节 1 (虚线) 与关节 2 (实线) 的跟踪误差 图 5 自适应辩识参数 10 15 20 0 5 15 20 25 30 10 30 1kg 600 400 200 0 -200 -400 -600 0 τ1 τ2 7 kg 3 kg 8 6 4 2 0 10 5 25 图 6 关节 1 与关节 2 的输入力矩 图 7 末端执行器变化的载荷 20 25 30 15 10 15 20 0 5 30 4 结论 本文介绍了在 Matlab/Simulink 环境下机器人控制系统 仿真的方法，这种建模方法得到的系统仿真框图与系统结构 大学出版社，2002． [2] 薛定宇，陈阳泉. 基于MATLAB/Simulink 的系统仿真技术与应用 [M]. 北京：清华大学出版社，2002． [3] 薛定宇．控制系统仿真与计算机辅助设计[M]．北京：机械工业出 版社，2004． 原理框图是相似的，更符合控制工程师研究问题的思路，而 [4] Haug E J. Computer_Aided Kinematics and Dynamics of Mechanical 且，复杂系统模块化的方法方便系统的结构设计和参数调 整，并能够实时观察系统运行的各个状态。 基于 M-Function 的方法通用性很强，几乎所有的控制 系统都可以采用这种方法来进行建模仿真，针对于 n 自由度 的机器人连杆系统，在建立机器人模型时，其工作量是非常 大的，而用 SimMechanics 模块组进行设计却显得非常简单 可靠，但是其参数在仿真运行过程中的改变相对于前者，缺 乏一定的灵活性。通过仿真，这两种方法在控制器和控制对 象参数相同的情况下，得出的结果是一致的。 参考文献： [1] John F G．机构动态仿真[M]．周进雄，张陵译．西安：西安交通 [5] System[M]．Englewood Cliffs，NJ：Prentice Hall，1989． Slotine J E, Li W．Composite adaptive control of robot manipulators [J]．Automatica, 1989，25(4), 509–519． [6] Berghuis H, Robbers H and Nijmeijers H. Experiment comparison of in adaptive robot control [J]. parameter estimation methods Automatica, 1995，31(9)：1275-1285. [7] Ortega R，Spong M W．Adaptive motion control of rigid robots：A tutorial [J]．Automatica，1989，25(6)：877–888． [8] MathWorks. SimMechanics for use with simulink user’s guide [Z]．Version 2，2002. [9] Yu T. Terminal sliding mode control for rigid robots [J]. Automatica, 1998, 34(1): 51-56. • 2025 •