动态规划（背包问题、最优装载问题等）.ppt

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：1.14M 资料格式：ppt 举报版权申诉

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第1页.png

第1页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第2页.png

第2页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第3页.png

第3页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第4页.png

第4页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第5页.png

第5页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第6页.png

第6页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第7页.png

第7页 / 共77页

f11b4dd6-2845-4428-81f4-3e061bdd8f8c.ppt.pdf-第8页.png

第8页 / 共77页

文本预览

第三章动态规划 2022-6-13

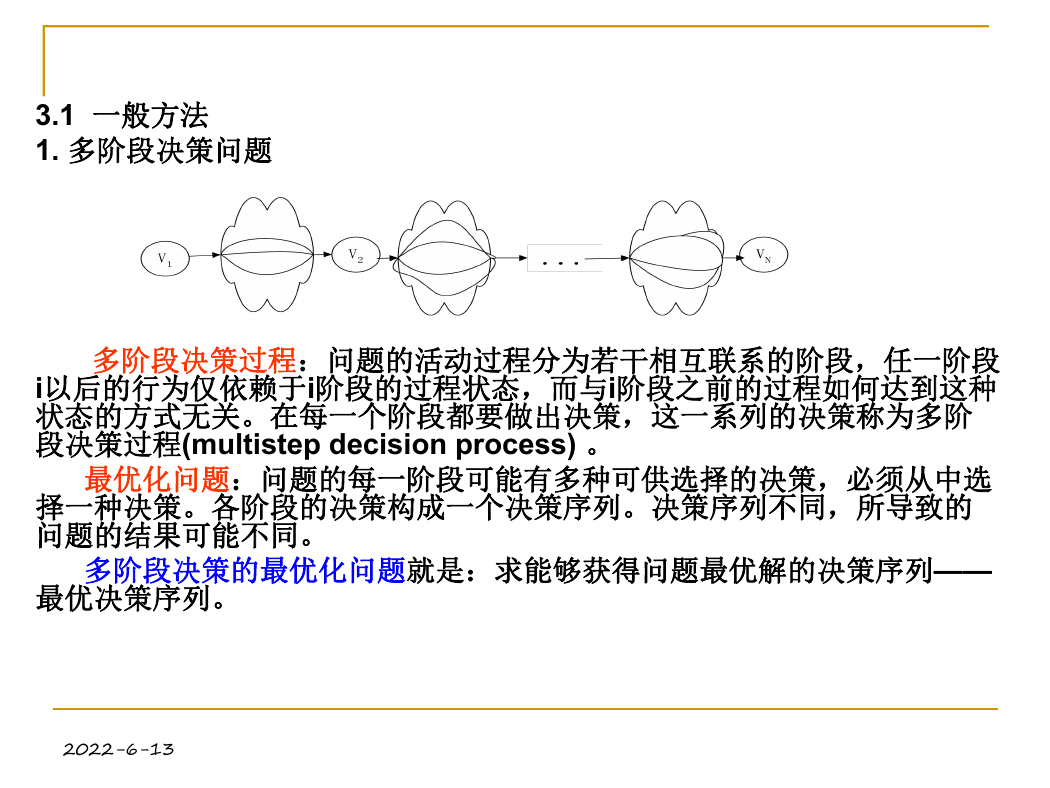
3.1 一般方法 1. 多阶段决策问题多阶段决策过程：问题的活动过程分为若干相互联系的阶段，任一阶段 i以后的行为仅依赖于i阶段的过程状态，而与i阶段之前的过程如何达到这种状态的方式无关。在每一个阶段都要做出决策，这一系列的决策称为多阶段决策过程(multistep decision process) 。最优化问题：问题的每一阶段可能有多种可供选择的决策，必须从中选择一种决策。各阶段的决策构成一个决策序列。决策序列不同，所导致的问题的结果可能不同。多阶段决策的最优化问题就是：求能够获得问题最优解的决策序列—— 最优决策序列。 2022-6-13

2. 多阶段决策过程的求解策略 1）枚举法穷举可能的决策序列，从中选取可以获得最优解的决策序列 2）动态规划 20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，创立了解决这类过程优化问题的新方法——动态规划。动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。应用领域：动态规划问世以来，在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动态规划方法比用其它方法求解更为方便。 2022-6-13

3. 最优性原理(Principle of Optimality) 过程的最优决策序列具有如下性质：无论过程的初始状态和初始决策是什么，其余的决策都必须相对于初始决策所产生的状态构成一个最优决策序列。利用动态规划求解问题的前提 1) 证明问题满足最优性原理如果对所求解问题证明满足最优性原理，则说明用动态规划方法有可能解决该问题 2) 获得问题状态的递推关系式获得各阶段间的递推关系式是解决问题的关键。 2022-6-13

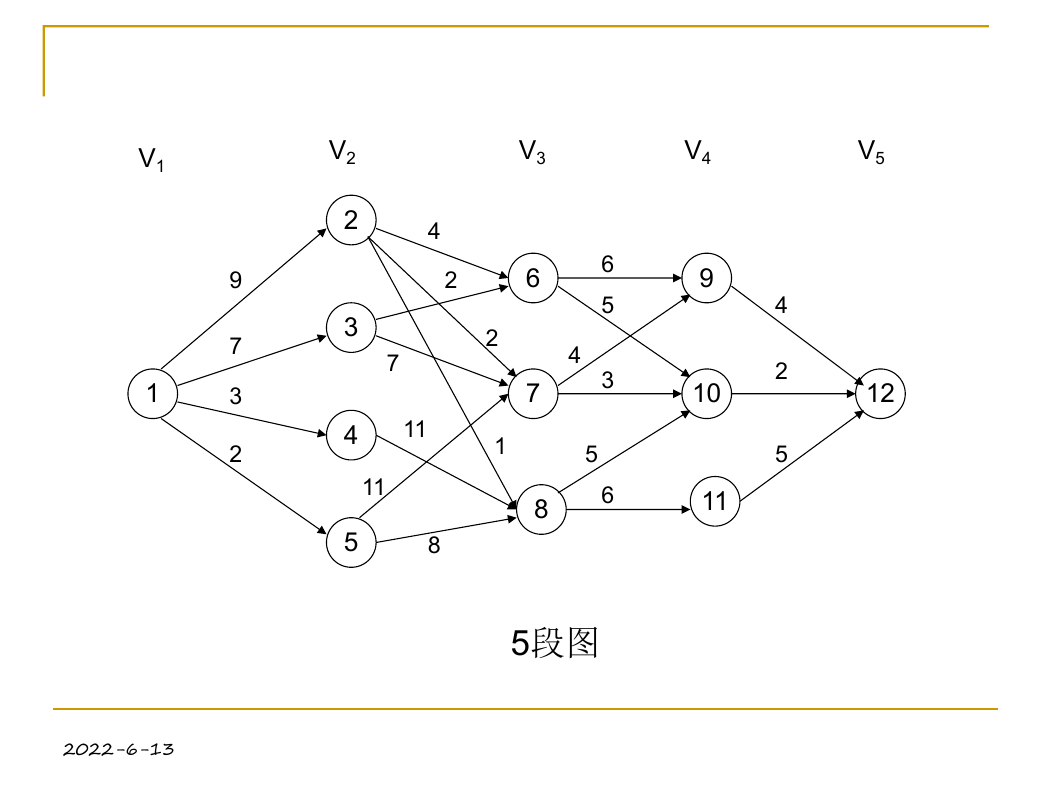
例3.1 [多段图问题]多段图G=(V,E)是一个有向图，且具有特性: 结点：结点集V被分成k≥2个不相交的集合Vi，1≤i≤k，其中V1和Vk分别只有一个结点s(源结点)和t(汇点)。 · 每一集合Vi定义图中的一段。边：所有的边(u,v)均具有如下性质：若∈E，则该边将是从某段i指向i+1段，即若u∈Vi，则v∈Vi＋1, 1≤i≤k－1。 · 每条边(u,v)均附有成本c(u,v)。 s到t的路径：从第1段开始，至第2段、第3段、…、最后在第k段终止。路径的成本是这条路径上边的成本和。多段图问题：求由s到t的最小成本路径。 2022-6-13

V1 1 9 7 3 2 V2 2 3 4 5 4 2 7 11 11 8 V3 6 7 8 2 1 6 5 3 6 4 5 5段图 V4 V5 9 10 11 4 2 5 12 2022-6-13

多段图问题的多阶段决策过程：生成从s到t的最小成本路径是在k-2个阶段（除s和t外）进行某种决策的过程：从s开始，第i次决策决定Vi+1(1≤i≤k-2)中的哪个结点在从s到t的最短路径上。最优性原理对多段图问题成立假设s,v2,v3,…,vk-1,t是一条由s到t的最短路径。 ● 初始状态：s ● 初始决策：(s,v2)， v2∈V2 ● 初始决策产生的状态：v2 则，其余的决策：v3,...,vk-1相对于v2将构成一个最优决策序列——最优性原理成立。反证：若不然，设v2,q3,…,qk-1,t是一条由v2到t的更短的路径，则s, v2,q3,…,qk-1,t将是比s,v2,v3,…,vk-1,t更短的从s到t的路径。与假设矛盾。故，最优性原理成立 2022-6-13

3.2 多段图问题 1. 问题的描述 ● 在多段图中求从s到t的一条最小成本的路径，可以看作是在k-2个段作出某种决策的结果。 ● 第i次决策决定Vi+1中的哪个结点在这条路径上，这里 1≤i≤k-2； ● 最优性原理对多段图问题成立 2022-6-13

分享到：

赞收藏

资料库

动态规划（背包问题、最优装载问题等）.ppt

相关推荐

课程资源

热门标签

最新资料