论文研究-基于EEF准则的三维空间声源个数估计 .pdf-资料库

中国科技论文在线基于 EEF 准则的三维空间声源个数估计# http://www.paper.edu.cn 朱慧佳，黄青华** （上海大学通信与信息工程学院，上海 200072）摘要：通过球麦克风阵列采集三维空间高阶声场信息，采用球谐函数分解声场并建立球阵列信号模型。然后利用 EEF 准则对信号源个数进行估计，避免过估计和欠估计问题。和传统信息论准则 MDL 作比较，仿真实验结果表明：EEF 准则能正确估计信号源个数，在低信噪比、低快拍数和声源到达方向角相距较近时，有更好的性能和优势。关键词：球麦克风阵列;源个数估计; EEF 准则中图分类号：TN911.7 Acoustic source number estimation based on EEF criterion in 3D space ZHU Huijia, HUANG Qinghua (School of Communication and Information Engineering, Shanghai University, Shanghai 200072) Abstract: Spherical microphone array is used to sample high-order sound field information in 3D space. The array signal model is constructed based on spherical harmonics decomposition of the sound field. Based on the model and exponentially embedded families (EEF) criterion, source number is estimated. The method can avoid over-estimate and under-estimate. Compared with the conventional minimum description length (MDL) criterion, computer simulation results demonstrate that EEF estimation method has better performance with respect to low signal-to-noise ratios, a small number of snapshots and closely spaced sources. Key words: spherical microphone array; source number estimation; EEF criterion 5 10 15 20 25 0 引言 30 35 源信号个数估计是模型阶数选择在阵列信号处理中的一个重要应用。它判断入射到阵列的空间源信号个数，是阵列信号处理的基本任务，在雷达、通信、声纳等领域受到越来越多的关注[1]。信号源个数的正确估计是阵列信号处理关键的第一步，决定着信源定位和分离等处理。目前广泛应用的一类信号源个数估计算法基于传统信息论准则，主要包括 Akaike 信息准则(AIC)和最小描述长度(MDL)准则[2,3]。AIC 存在两个问题：一是在低快拍数的情况下该算法存在过估计；二是该算法不满足一致性估计。而 MDL 准则在满足一致性估计的前提下，在低快拍数和低信噪比的条件下存在欠估计问题[4]。2005 年 Kay 提出了一种新的模型阶数估计方法，此方法基于指数嵌入族(EEF)理论和充分统计量[5]。EEF 准则能更好地克服上述算法的缺点，在保证一致性的前提下，不存在过估计和欠估计的问题，并且计算复杂度与 MDL 相似。2008 年 Xu 等人将 EEF 模型选择理论用于源个数估计[6]，他们采用均匀线阵列估计平面内的信源数目。随着三维音频的发展，三维空间中多信源的个数估计和处理具有重要意义。球麦克风阵列被用于采集空间声场信息，它具有三维空间的旋转对称结构和较高的空间分辨率，能够对声场进行更加充分的采样[7,8]。基金项目：教育部博士点基金（No. 20093108120018）；国家自然科学基金（No.61001160）作者简介：朱慧佳(1990-)，女，主要研究方向：阵列信号处理通信联系人：黄青华(1978-)，女，副研究员，主要研究方向：阵列信号处理，3D 音频，盲信号处理. E-mail: qinghua@shu.edu.cn - 1 -

40 45 中国科技论文在线 http://www.paper.edu.cn 本文利用球麦克风阵列采集空间声场高阶信息，建立球阵列信号模型。在此基础上，采用 EEF 准则进行信号源个数估计。同时将传统算法 MDL 和 EEF 方法进行性能比较。通过计算机仿真实验，验证 EEF 算法具有更好的性能。 1 球阵列信号模型为了能准确估计三维空间中源信号的个数，采用球麦克风阵列来获取空间声场信息。假设 L 个相互独立、各向同性的麦克风分布在半径为 R 的球面上。建立球坐标系，如图 1 所示。球麦克风阵列的球心为坐标系原点O ，位于球面l 点处的阵元采用它的俯仰角和方位角 Ω = 表示。 ( ) lθ φ l , l 50 图 1 球坐标系 Fig. 1 Spherical coordinate system 假设在远场条件下，从 dϑ ϕ=Φ , 处的频域声压采用球谐函数分解为： ( d d ) 方向入射一波数为 k 的单位幅度平面波，其在阵元l 55 60 65 式中“*”表示共轭， ( , ) m ∞ n l 0 n d = , ) ) ( ∑ p k ( , b kR d n Φ Ω = ∑ nY θφ 是 n 阶 m 级球谐函数， n m n m 1) ( ( n + 4 π ( , ) θφ Y m n − + m n =− (2 = Y m [ n ( Φ )] * Y m n ( Ω l d ) (1) )! )! m P n (cos ) im φθ e (2) m nP (cos ) θ 是关联勒让德多项式， ( ) nb kR 为远场模态强度， ⎧ ⎪ = ⎨ ⎪⎩ ⎞ ) ⎟ ⎠ ) ⎛ ⎜ ⎝ j kR n j kR n ( j kR ' n h kR ' n h kR n i 4 π i 4 π ( ( ) ) − ( ) ( n n b kR n ( ) ) ) nh kR 分别是球贝塞尔函数和球汉克尔函数， ' ( nj kR 和 ( ( ) 在实际应用中，阶数 n 不可能取无穷大。一般地，阶数取为 N 整数[7]。刚性球 (3) 开放球 nj ka 和 ' ( nh ka 分别对应它们的导数。 ) kR= ⎡ ⎥ ， ⋅⎡ ⎤⎢ ⎥ 表示向上取最大 ⎤ ⎢ 考虑到实际环境中存在噪声，设加性噪声是具有零均值的复高斯随机过程，且满足噪声和信号互相独立的特性。若有 D 个声源同时入射到球阵列，由此得到的球阵列接收信号模型为： x As n (4) 其中 x 是一个 L 维的阵列观测信号向量，s 是一个 D 维的源信号向量，n 是一个 L 维的噪声 = + - 2 -

中国科技论文在线 http://www.paper.edu.cn 向量，A 是一个 L D× 维的导向矩阵，它描述源信号到阵元的空间传输特性。根据式(1)，导向矩阵可分解为： =A Y(Ω)BY (Φ) (5) H 70 其中 Y(Ω) 是一个 L N× ( 2 + 维的球谐矩阵， 1) B 是一个 ( N 2 + 1) × ( N 2 + 1) Y ( Ω = ) Y Y Y ( ( ) ) N 1 0 ⎡ Ω Ω Ω L N 1 1 1 1 0 ⎢ Ω Y Y Y N ) ( ( ) 1 0 Ω Ω L N 1 0 2 ⎢ M O M ⎢ Y Y Y N ( ) ) 1 0 Ω ⎣ L N L 1 0 Y ) 0 1 Y ) 0 1 Y ) 0 1 ( Ω 1 ( Ω 2 M ( Ω ( L L Ω ) ) 2 ) L (6) ⎤ ⎥ ⎥ ⎥ ⎦ 2 ( ( M ( Ω Y ( ) 1 − Ω 1 1 Y ) ( 1 − Ω 2 1 M Y ( ) 1 − Ω 1 的对角矩阵， , =B L diag b ( 0 { 1 , b n b N , , L L L L N 1 + b b , , , , n N 14243 14243 )Y Ω 结构相同[9]。 1 + n 2 2 ) (7) )Y Φ 是一个 ( D N× ( 2 + 维的球谐矩阵，与 ( 1) 75 球阵列接收数据的协方差矩阵为： xx E H { } AR A H s = = R = + H } A ss A E { R n H + nn E { H } (8) 其中 sR 为信号协方差矩阵， nR 为噪声协方差矩阵，设噪声方差为 2 nσ ，所以在实际应用中，R 由 J 个球麦克风阵列的采样值 ( )jx R AR A = H + s 2 nσ I (9) = L )的采样协方差矩阵来 1,2, J ( j , 80 估计，对 ˆR 进行特征值分解 1 J ˆ = ∑R J = j 1 x j ( ) x H j ( ) (10) 2 , , , λ λ λL 是 L 个特征值， 1 式中 1 2 基于 EEF 准则的声源个数估计 c c 2, , L 85 c c (11) l H l L λ l ˆ = ∑R cL 是对应的特征向量。 , L 1 = l 用 0H 表示参考模型，即没有源信号。假设候选的源信号个数 { ∈ ， dH 表示球阵列接收数据中有 d 个源信号时的模型。d 个源信号入射到接收阵列时的阵列协方差矩阵用 ( )dR 来表示： L −L 0,1, } 1 d , 90 用 ( )dα 来表示模型 dH 的参数 d ) ( d ∑R = i 1 = ( μ i − σ n 2 ) v v i i H + σ n 2 I (12) μ μ μ 和 1 = v 分别是 ( d 其中 1 布的零均值复高斯随机变量，对它进行 J 次采样 (1), (2),..., ( )J μ μ μ d (13) )dR 的特征值和特征向量。假设观测向量 x 是独立同分 x ，则联合概率密度函数为： v v T , 1 v v , , 2 σ n ,..., ,..., ,..., ,..., α x x v T d T 2 , , , d d 1 2 2 2 ( ) ( ) x J (1), (2),..., ( ) ( f J ∏ j 1 = )dα 无关的项略去，进行最大化求解，可以得到 ( 将上式取对数，并将与参数向量 ( 似然估计[10]： ) R ⎡ ⎣ 1 det( exp j ( ) j ( ) L π R H ( ) α = − x x x x ⎤ ⎦ 1 − ) , H d d d d ( ) ( ) ( ) 95 (14) )dα 的最大 ˆ μ λ= i i i = L d 1,2, , - 3 -

中国科技论文在线 http://www.paper.edu.cn 2 ˆ σ n ˆ v i = = L 1 − ∑ (15) L d i d 1 = + c i 1,2, = λ i , L d i 所以，对数似然函数可表示如下： ) ) α L ( d ( = ln J = − ⎞ ⎟ ⎠ 在参考模型 0H 条件下，对数似然函数可表示为： x 1 L ( f ⎡ J L = − ⎢ ⎣ ⎛ ⎜ ⎝ ln ln α L = x (0) ( ) i 定义一个似然比函数 ( L d 如下： ) x ( ln f ⎡ ⎢ ⎣ d x x J (1), (2),..., ( ) ⎛ ∏ ⎜ ⎝ L d λ i + − 1 = ( ) ) d , α H ( d 1 ⎛ ⎜ L d −⎝ )ln L ∑ λ i i d 1 = + (16) ⎞ ⎟ ⎠ ⎤ ⎥ ⎦ α H (0) , ) 0 (17) J (1), (2),..., ( ) x ⎤ ⎞ ⎥ ⎟ ⎠ ⎦ L ∑ i 1 = λ i ( L d ) = 2 则 EEF 准则[6]表示如下： α L ( ( α L ( d ) (0) ) ) (18) EEF d ( ) = L d ( ) − n d ⎧ ⎪ ⎨ ⎪ ⎩ ln ⎡ ⎢ ⎢ ⎣ ⎛ ⎜ ⎝ L d ( ) n d ⎞ ⎟ ⎠ + ⎤ 1 ⎥ ⎥ ⎦ ⎫ ⎪ ⎬ ⎪ ⎭ u ⎛ ⎜ ⎝ L d ( ) n d − 1 ⎞ ⎟ ⎠ 式中 dn 是参数向量 ( )dα 的自由度 (19) + (20) ) 1 EEF d 的最大值对应的 d 为源信号的个数。 d L d (2 ( ) dn = − 选择传统经典信息论准则 MDL[10]表示如下： 100 105 110 MDL d ( )= − α ( L ( d ) )+ n d ln J (21) 1 2 当取最小描述长度 MDL d 最小值对应的值 d 即为所估计的信号源个数。当 d D= 时， ( ) 115 源信号个数被正确估计。 3 仿真实验仿真实验采用一个半径 R=5 cm，阵元数为 32 元的均匀球麦克风阵列[7]。通过 MATLAB 仿真进行 3 组实验。采用 Monte Carlo 实验方法，以正确个数估计的概率作为评价指标。验证在同等环境和相同条件下，基于 EEF 准则的空间信号源个数估计，相比于传统的 MDL 准则有更高的正确估计概率。假设 3 个单位幅度的平面波分别从三个不同的方向入射到球麦克风阵列。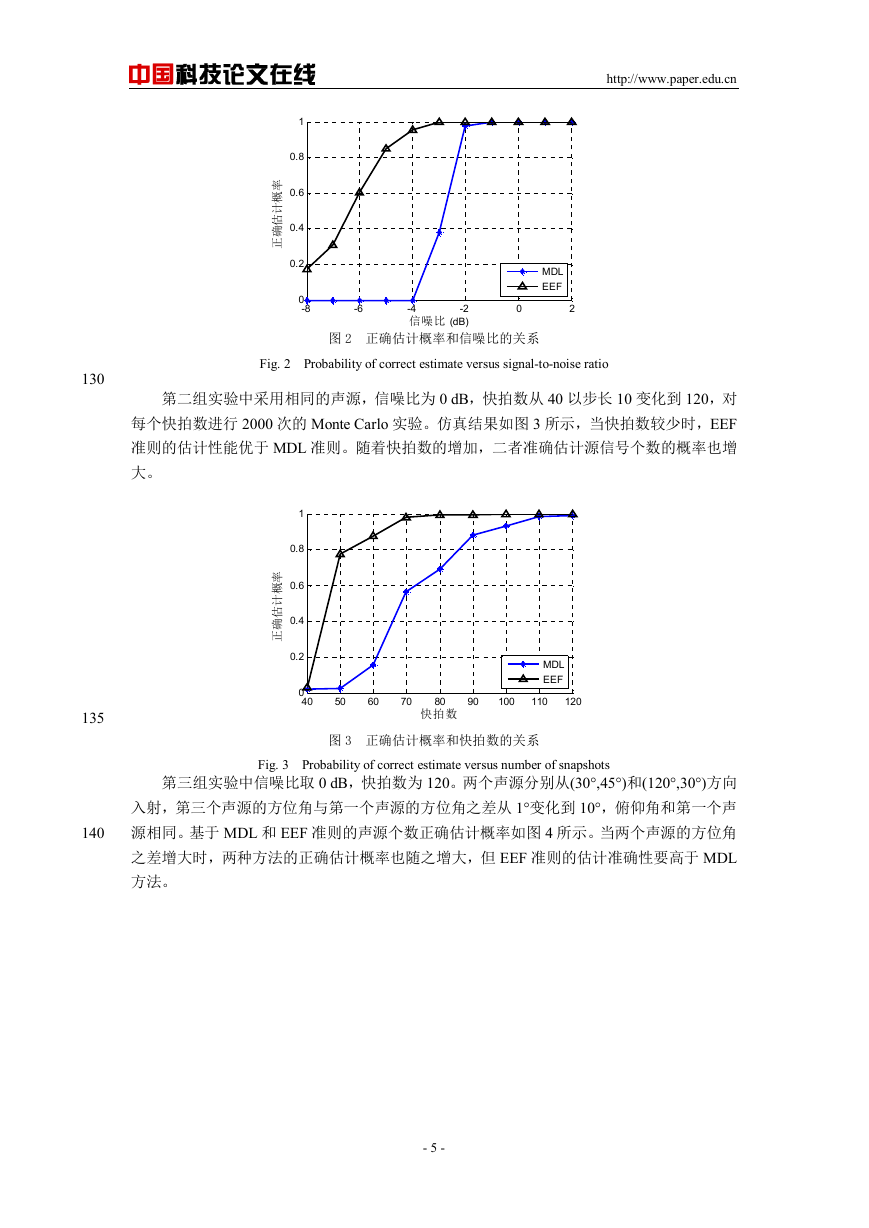第一组实验中三个声源分别从(30°,45°), (60°,240°)和(120°,30°)方向入射，快拍数取 120，信噪比从-8 dB 以步长 1 dB 变化到 2 dB。对每个信噪比值进行 2000 次的 Monte Carlo 实验。源个数正确估计的概率和信噪比变化的关系如图 2 所示。当信噪比在 0 dB 以下时，EEF 准则估计源信号个数的性能要优于 MDL 准则。随着信噪比的增大，两种方法正确估计的概率增大。当噪声较小时，两种方法都能准确估计出源信号的个数。 120 125 - 4 -

130 135 140 中国科技论文在线 http://www.paper.edu.cn 1 0.8 0.6 0.4 0.2 率概计估确正 0 -8 -6 -4 -2 信噪比 (dB) MDL EEF 0 2 图 2 正确估计概率和信噪比的关系 Fig. 2 Probability of correct estimate versus signal-to-noise ratio 第二组实验中采用相同的声源，信噪比为 0 dB，快拍数从 40 以步长 10 变化到 120，对每个快拍数进行 2000 次的 Monte Carlo 实验。仿真结果如图 3 所示，当快拍数较少时，EEF 准则的估计性能优于 MDL 准则。随着快拍数的增加，二者准确估计源信号个数的概率也增大。率概计估确正 1 0.8 0.6 0.4 0.2 0 40 MDL EEF 50 60 70 80 90 100 110 120 快拍数图 3 正确估计概率和快拍数的关系 Fig. 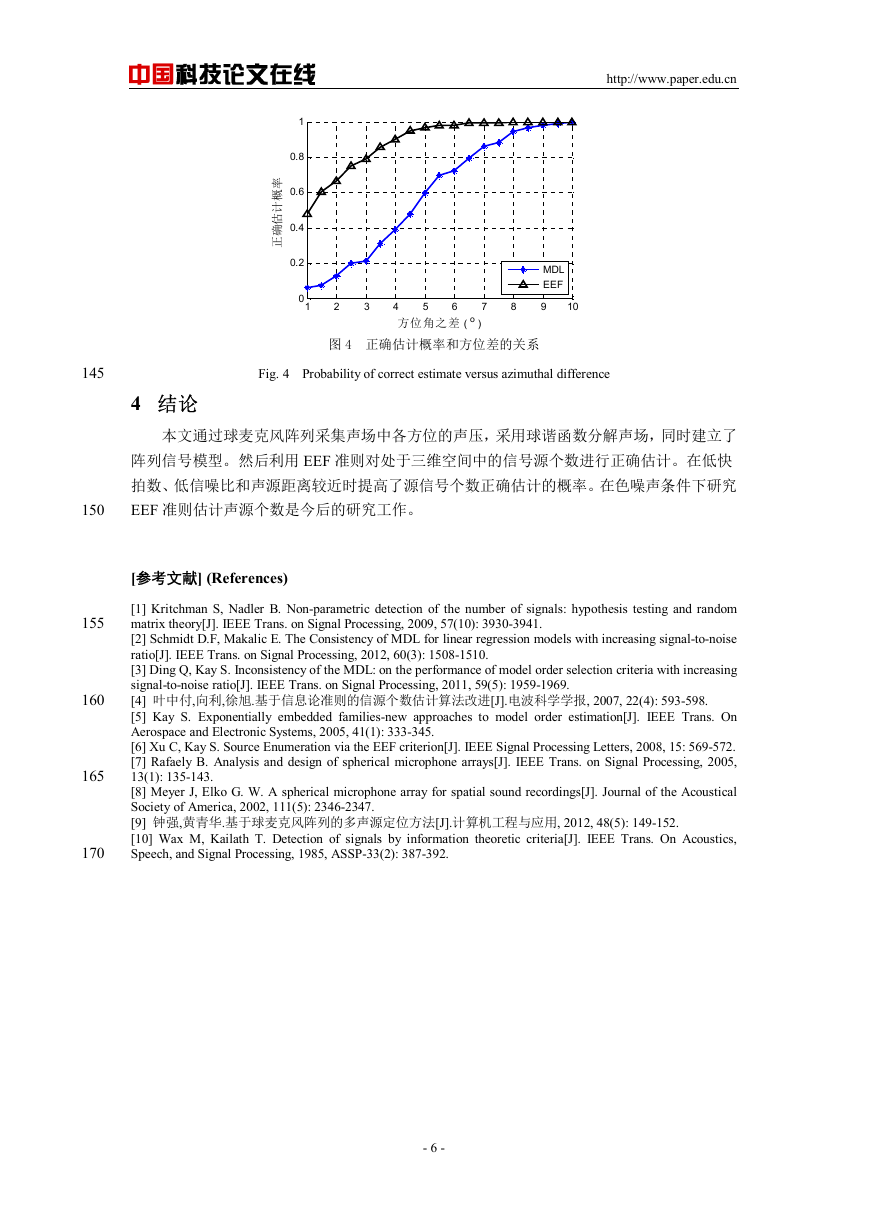3 Probability of correct estimate versus number of snapshots 第三组实验中信噪比取 0 dB，快拍数为 120。两个声源分别从(30°,45°)和(120°,30°)方向入射，第三个声源的方位角与第一个声源的方位角之差从 1°变化到 10°，俯仰角和第一个声源相同。基于 MDL 和 EEF 准则的声源个数正确估计概率如图 4 所示。当两个声源的方位角之差增大时，两种方法的正确估计概率也随之增大，但 EEF 准则的估计准确性要高于 MDL 方法。 - 5 -

中国科技论文在线 http://www.paper.edu.cn 1 0.8 0.6 0.4 0.2 率概计估确正 0 1 2 3 MDL EEF 7 8 9 10 5 4 方位角之差 ( o ) 6 145 150 155 160 165 170 图 4 正确估计概率和方位差的关系 Fig. 4 Probability of correct estimate versus azimuthal difference 4 结论本文通过球麦克风阵列采集声场中各方位的声压，采用球谐函数分解声场，同时建立了阵列信号模型。然后利用 EEF 准则对处于三维空间中的信号源个数进行正确估计。在低快拍数、低信噪比和声源距离较近时提高了源信号个数正确估计的概率。在色噪声条件下研究 EEF 准则估计声源个数是今后的研究工作。 [参考文献] (References) [1] Kritchman S, Nadler B. Non-parametric detection of the number of signals: hypothesis testing and random matrix theory[J]. IEEE Trans. on Signal Processing, 2009, 57(10): 3930-3941. [2] Schmidt D.F, Makalic E. The Consistency of MDL for linear regression models with increasing signal-to-noise ratio[J]. IEEE Trans. on Signal Processing, 2012, 60(3): 1508-1510. [3] Ding Q, Kay S. Inconsistency of the MDL: on the performance of model order selection criteria with increasing signal-to-noise ratio[J]. IEEE Trans. on Signal Processing, 2011, 59(5): 1959-1969. [4] 叶中付,向利,徐旭.基于信息论准则的信源个数估计算法改进[J].电波科学学报, 2007, 22(4): 593-598. [5] Kay S. Exponentially embedded families-new approaches to model order estimation[J]. IEEE Trans. On Aerospace and Electronic Systems, 2005, 41(1): 333-345. [6] Xu C, Kay S. Source Enumeration via the EEF criterion[J]. IEEE Signal Processing Letters, 2008, 15: 569-572. [7] Rafaely B. Analysis and design of spherical microphone arrays[J]. IEEE Trans. on Signal Processing, 2005, 13(1): 135-143. [8] Meyer J, Elko G. W. A spherical microphone array for spatial sound recordings[J]. Journal of the Acoustical Society of America, 2002, 111(5): 2346-2347. [9] 钟强,黄青华.基于球麦克风阵列的多声源定位方法[J].计算机工程与应用, 2012, 48(5): 149-152. [10] Wax M, Kailath T. Detection of signals by information theoretic criteria[J]. IEEE Trans. On Acoustics, Speech, and Signal Processing, 1985, ASSP-33(2): 387-392. - 6 -

资料库

论文研究-基于EEF准则的三维空间声源个数估计 .pdf

相关推荐

开发技术

热门标签

最新资料