一类混沌系统的同步、反同步及在保密通信中的应用.pdf-资料库

http://www.paper.edu.cn 一类混沌系统的同步、反同步及在保密通信中的应用1 王兴元，王甲纲大连理工大学电子与信息工程学院，大连（116024）摘要：研究了一类自治混沌系统的同步问题．基于 Lyaponuv 稳定性理论，提出了一种新的线性分离的同步方法，并采用该方法实现了一类自治混沌的完全同步和反同步．最后将该方法应用于保密通信中．通过对耦合发电机系统的数据模拟，进一步验证了该方法的有效性．关键词：同步，反同步，线性分离，耦合发电机系统，混沌保密通信．中图分类号：TP301.5 PACC：0545，0555 0. 引言 1990年，Pecora和Carroll提出了在初始条件不同的情况下两个相同的混沌系统的自同步方法[1]．由于混沌同步在信息科学、医学、生物、工程等领域具有很大的应用潜力及发展前景，引起了人们的广泛关注与兴趣，科学工作者在理论和实验上都已做了大量的工作[2-7]．混沌同步，研究的是如何使两个混沌系统达到同步，典型的同步方法有PC法、反馈法、观测器法、神经网络控制法、T-S模糊模型法等[8-11]．就目前混沌同步方法论的发展所取得的成就而言，上述方法并不是对所有混沌系统的控制或同步都有效，不同的方法有各自的优缺点，具体情况要具体分析[12-18]．为此，本文利用线性分离方法实现了耦合发电机系统的同步和反同步，并将反同步方法应用于保密通信中．数值仿真结果进一步证实了该方法的有效性． 1. 基于线性分离的混沌同步 1.1 混沌系统的分离自治混沌系统可以描述为 t t ( ), ) : n ， (1) → n 定义了一个 n 维矢量空间的矢量域．把这里函数 x f n t ∈ ¡ ( ) x t t ( ), ) ( f =&x t ( ) x ( f 是系统的 n 维状态矢量，分解为 f x t ( ( ), ) g = t x ( ( )) t + h x t ( ( ), ) t ， (2) 这里 x t t f 是 ( ( ), ) x t t h ( ( ), ) = 1.2 同步 t g = x ( ( )) Ax ， (3) 的线性部分；是常满秩矩阵，并且它的所有的特征值实部都是负的，所以 x f t ( ( ), ) t ( ) 的非线性部分．这样系统(3)可以被重写为 t ． (4) A x x g t f t t ( ( )) ( ( ), ) 是 &x x x t g t t ( ( ), ) ( ( )) ( ) + = h − t 本文所提到的完全同步指的是两个相关系统的状态矢量之差最终趋于零．对于给定的系统(4)，构造一个新的系统为 1本课题得到国家自然科学基金(编号：60573172)和辽宁省教育厅高等学校科学技术研究项目(编号： 20040081)的资助。 -1-

http://www.paper.edu.cn n t ( h g x + = &y t ( ) t t ( ), ) y ( ( )) ， (5) y t ∈¡ ( ) 是系统 (5) 的 n 维状态矢量．系统 (1) 与系统 (5) 的同步误差被定义为这里 ty ，则误差系统的解由下面的等式来确定 x e t t ( ) ( ) ( ) − = & & x Ay e t t g ( ) ( ) − − = ( )te A 由式(6)可知的零点就是线性系统的稳定判定准则知，同步误差系统(6)在零点是渐进稳定的，并且有 Ae ． (6) − 的平衡点．因为矩阵的所有特征值的实部都为负，根据 x t ( ( )) ( )t&e y ( ( )) & y t ( ) Ax t ( ) t ( ) t ( ) ， = = = g t = 0 e t lim ( ) t →∞ 即系统(1)的状态矢量 ( )tx 和系统(5)的状态矢量 ( )ty 达到同步． 1.3 反同步反同步指的是两个同步系统的状态矢量的值相同，但符号相反．如果系统和满足 1S 2S 下列等式，则两系统反同步： + y t ( ) = 0 ， (7) x t lim ( ) t →∞ 1S t ( ) 2S y g ( ( )) e t 这里 ( )tx 和 ( )ty 分别表示和的状态矢量．构造一个新的系统为： h ( − t 定义系统(1)与系统(8)的反同步误差为 ( ) = 确定 = y x t t ( ), ) x t ( ) + ． (8) y ，则误差系统的解由下面的等式来 t ( ) = + & e t ( ) & y t ( ) & x t ( ) ( )te g 的零点就是 = 由式(9)可知线性系统的稳定判定准则知，反同步误差系统(8)在零点是渐进稳定的，并且有 li t Ae ． (9) 的平衡点．因为矩阵的所有特征值的实部都为负，根据 0 x t ( ( )) ( )t&e Ay + A t m ( ) →∞ y ( ( )) Ax t ( ) t ( ) t ( ) + = = = g e t ，即系统(1)的状态矢量 ( )tx 和系统(8)的状态矢量 ( )ty 达到反同步． 2. 数值模拟以如下的耦合发电机系统 & x x μ = − + ⎧ 1 1 ⎪ & x x μ + = − ⎨ 2 2 ⎪ = − & x x x 1 ⎩ 1 2 3 x x ( 2 3 x x ( 1 3 ) α + ) α − (10) 为例进行数值模拟．当参数 1μ= 和 1.9α= 时，系统(10)是混沌的．用 ( ( )) 系统(10)进行分解．其中 tx 和 g g h h ( tx ( )) 将 tx 和 ( ( )) μ −⎛ ⎜ 0 ⎜ ⎜ 0 ⎝ = ) tx ( ( )) 分别为 x 0 0 1 x 0 − μ 2 x 0 β − 3 ⎞⎛ ⎟⎜ ⎟⎜ ⎟⎜ ⎠⎝ ⎞ ⎟ ⎟ ⎟ ⎠ = A x 1 x 2 x 3 ⎛ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎠ ， (11) g x x x ( , 3 , 1 2 和 h x x x t ( , ) , , 1 2 3 ⎛ ⎜= ⎜ ⎜ ⎝ 1 x x 2 3 x x 1 3 x β + 3 x + α 2 x − α 1 x x − 1 2 ⎞ ⎟ ⎟ ， (12) ⎟ ⎠ -2-

http://www.paper.edu.cn A ( 这里具有负的实特征值 & y 1 & y 2 & y 3 ⎧ ⎪ ⎨ ⎪ ⎩ , , ) − − − ．构造新系统为 μ μ β y x x ( = − μ 1 2 3 y x x ( μ = − 1 3 y x ( β β = − 3 3 ) + α ) α − 1 + − + + + x x 2) 1 2 ． (13) A 由于 e t lim ( ) = t →∞ 的特征值为负实数，根据线性系统的稳定判定准则知误差 lim[ t →∞ ，即系统(10)与系统(13)实现了同步． t ( )] t ( ) − = x 0 y 2 = = = = x 3 y 2 y 3 x 2 (0) (0) (0) (0) (0) τ= (0) 1 = ，系统参数为选取时间步长为 0.001s 的特征值必须全为负实数．由于已选取，采用四阶 Runge-Kutta 法来求解三维自治方程组(10)和 = 和 1μ= 和 1.9α= ．要使系统(10)与系统(13)实现同步， 1μ= ，故只要取β为正实数即可，本文分别取 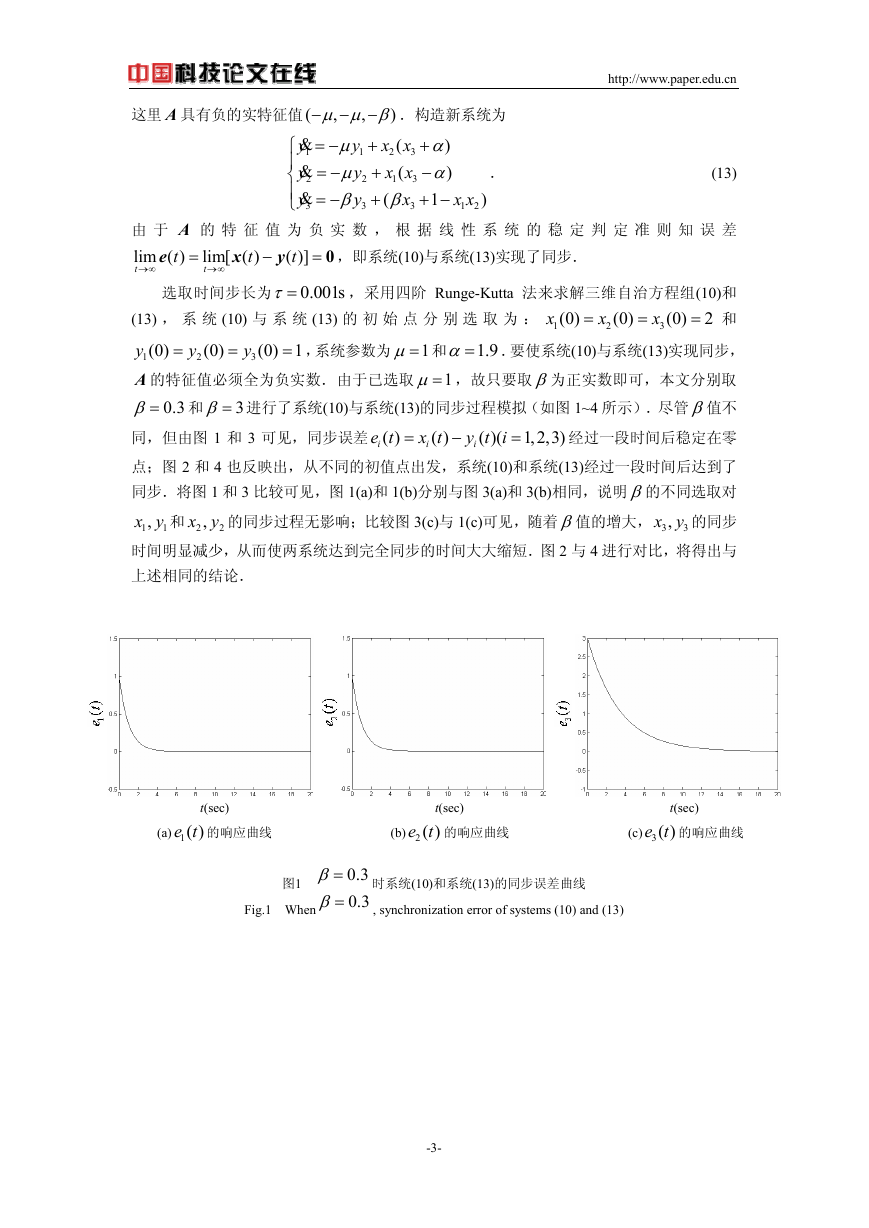3β= 进行了系统(10)与系统(13)的同步过程模拟（如图 1~4 所示）．尽管β值不 x (13) ，系统(10) 与系统(13) 的初始点分别选取为： 1 y 1 A 0.3β= 和同，但由图 1 和 3 可见，同步误差经过一段时间后稳定在零点；图 2 和 4 也反映出，从不同的初值点出发，系统(10)和系统(13)经过一段时间后达到了 β的不同选取对同步．将图 1 和 3 比较可见，图 1(a)和 1(b)分别与图 3(a)和 3(b)相同，说明 ,x y 和 2 ,x y 的同步时间明显减少，从而使两系统达到完全同步的时间大大缩短．图 2 与 4 进行对比，将得出与上述相同的结论． ,x y 的同步过程无影响；比较图 3(c)与 1(c)可见，随着β值的增大， 3 1,2,3) x t ( ) i e t ( ) i i ( )( y t i 1 1 = − = 2 3 t(sec) t (sec) t(sec) e t 1( ) 的响应曲线 (b) 的响应曲线 (c) e t 3( ) 的响应曲线 (a) e t 2( ) 图1 Fig.1 When 0.3β= 0.3β= 时系统(10)和系统(13)的同步误差曲线 , synchronization error of systems (10) and (13) -3-

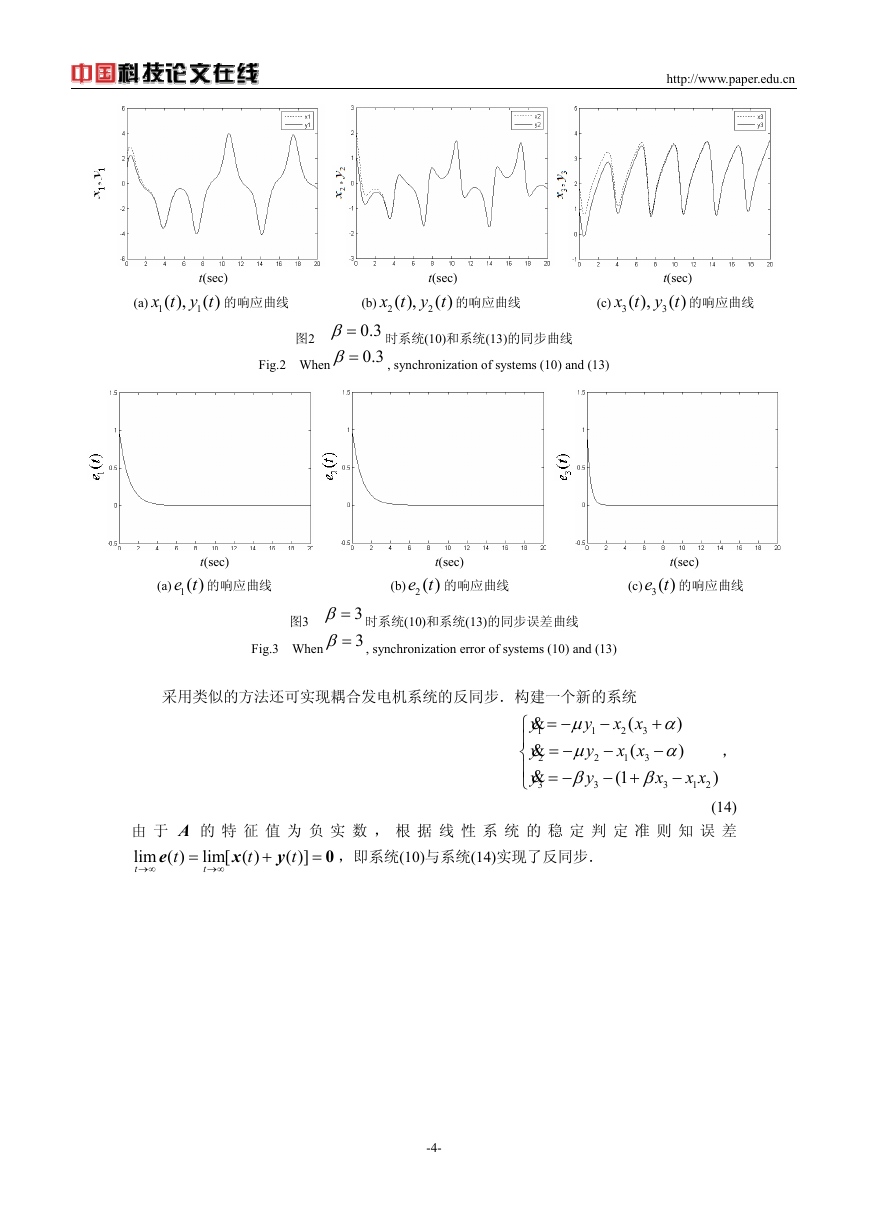
t(sec) t (sec) t(sec) ( ) ( ), x t y t 的响应曲线 (c) 2 x t y t 的响应曲线 3 ( ), ( ), ( ) 2 3 (a) 1 1 ( ) x t y t 的响应曲线 (b) 0.3β= 0.3β= 图2 Fig.2 When 时系统(10)和系统(13)的同步曲线 , synchronization of systems (10) and (13) http://www.paper.edu.cn t(sec) t (sec) t(sec) e t 1( ) 的响应曲线 (b) 的响应曲线 (c) e t 2( ) e t 3( ) 的响应曲线 (a) 图3 Fig.3 When 3β= 时系统(10)和系统(13)的同步误差曲线 3β= , synchronization error of systems (10) and (13) 采用类似的方法还可实现耦合发电机系统的反同步．构建一个新的系统 x x ( ) − + α 2 3 x x ) ( α − − 3 1 x (1 β − + − 3 ) (14) 的特征值为负实数，根据线性系统的稳定判定准则知误差 lim[ t →∞ ，即系统(10)与系统(14)实现了反同步． y μ 1 y μ y β 3 = − = − = − & y 1 & y 2 & y 3 ⎧ ⎪ ⎨ ⎪ ⎩ t ( )] t ( ) x 2 x 1 = + x 0 y 2 ， A 由于 e t lim ( ) = t →∞ -4-

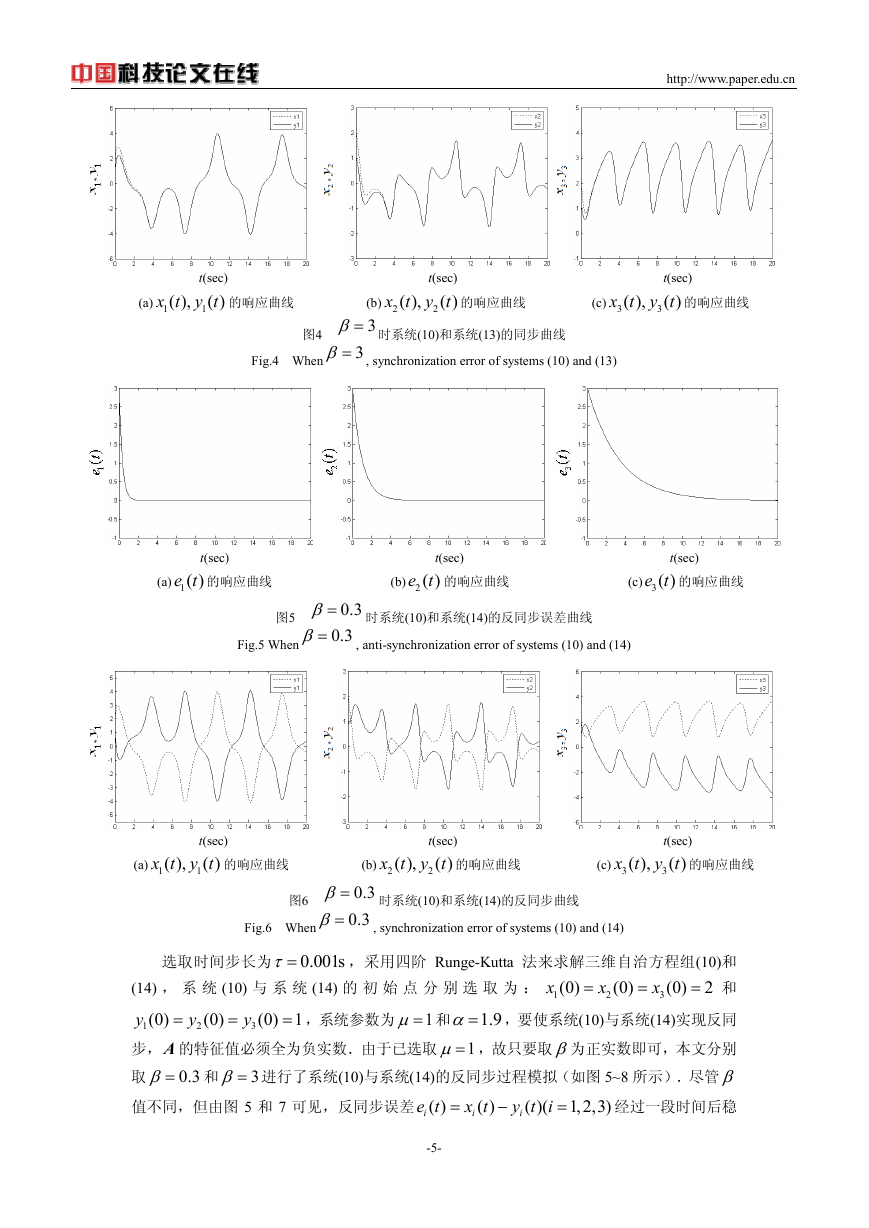
http://www.paper.edu.cn t(sec) t (sec) t(sec) ( ), x t y t 的响应曲线 (b) x t y t 的响应曲线 (c) 2 x t y t 的响应曲线 3 ( ), ( ), ( ) ( ) ( ) 1 2 3 (a) 1 图4 3β= 时系统(10)和系统(13)的同步曲线 3β= , synchronization error of systems (10) and (13) Fig.4 When t(sec) t (sec) t(sec) e t 1( ) 的响应曲线 (b) 的响应曲线 (c) e t 2( ) e t 3( ) 的响应曲线 (a) 图5 0.3β= 0.3β= 时系统(10)和系统(14)的反同步误差曲线 Fig.5 When , anti-synchronization error of systems (10) and (14) t(sec) t (sec) t(sec) ( ) ( ), x t y t 的响应曲线 (c) 2 x t y t 的响应曲线 3 ( ), ( ), ( ) 1 2 3 (a) 1 ( ) x t y t 的响应曲线 (b) 0.3β= 0.3β= 图6 Fig.6 When 时系统(10)和系统(14)的反同步曲线 , synchronization error of systems (10) and (14) τ= 选取时间步长为 0.001s ，采用四阶 Runge-Kutta 法来求解三维自治方程组(10)和 x = 和 (14) ，系统(10) 与系统(14) 的初始点分别选取为： 1 1μ= 和 1.9α= ，要使系统(10)与系统(14)实现反同 y 1 步，A 的特征值必须全为负实数．由于已选取 1μ= ，故只要取β为正实数即可，本文分别 3β= 进行了系统(10)与系统(14)的反同步过程模拟（如图 5~8 所示）．尽管β 取 0.3β= 和，系统参数为 (0) 1 = (0) (0) (0) (0) (0) x 2 y 3 x 3 = = = = 2 y 2 值不同，但由图 5 和 7 可见，反同步误差 e t ( ) i = x t ( ) i − y t i i ( )( = 1,2,3) 经过一段时间后稳 -5-

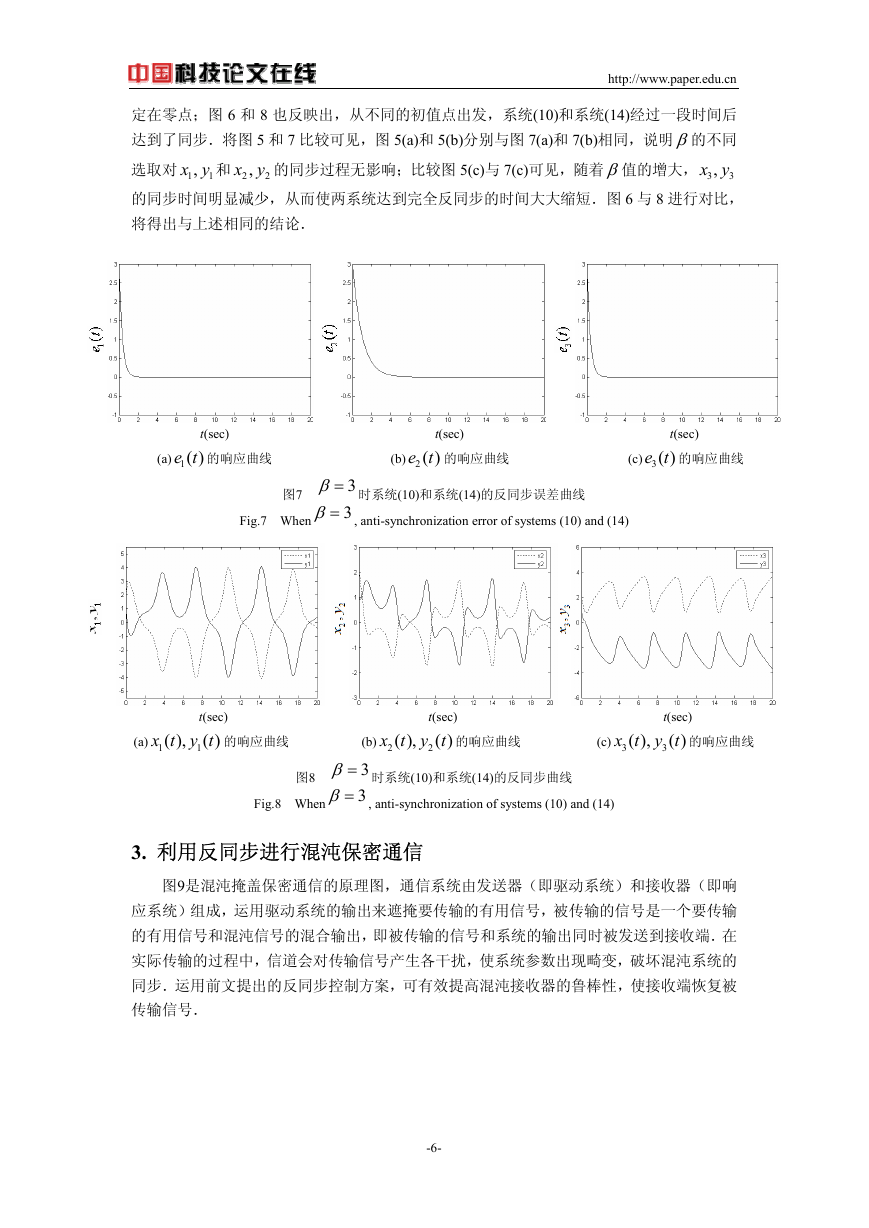
http://www.paper.edu.cn 定在零点；图 6 和 8 也反映出，从不同的初值点出发，系统(10)和系统(14)经过一段时间后达到了同步．将图 5 和 7 比较可见，图 5(a)和 5(b)分别与图 7(a)和 7(b)相同，说明β的不同 ,x y 选取对 1 3 的同步时间明显减少，从而使两系统达到完全反同步的时间大大缩短．图 6 与 8 进行对比，将得出与上述相同的结论． ,x y 的同步过程无影响；比较图 5(c)与 7(c)可见，随着β值的增大， 3 ,x y 和 2 1 2 t(sec) t (sec) t(sec) e t 1( ) 的响应曲线 (b) 的响应曲线 (c) e t 2( ) e t 3( ) 的响应曲线 (a) 图7 Fig.7 When 3β= 时系统(10)和系统(14)的反同步误差曲线 3β= , anti-synchronization error of systems (10) and (14) t(sec) t (sec) t(sec) ( ) ( ), x t y t 的响应曲线 (b) x t y t 的响应曲线 (c) 2 x t y t 的响应曲线 3 ( ), ( ), ( ) ( ) 1 2 3 (a) 1 图8 Fig.8 When 3β= 时系统(10)和系统(14)的反同步曲线 3β= , anti-synchronization of systems (10) and (14) 3. 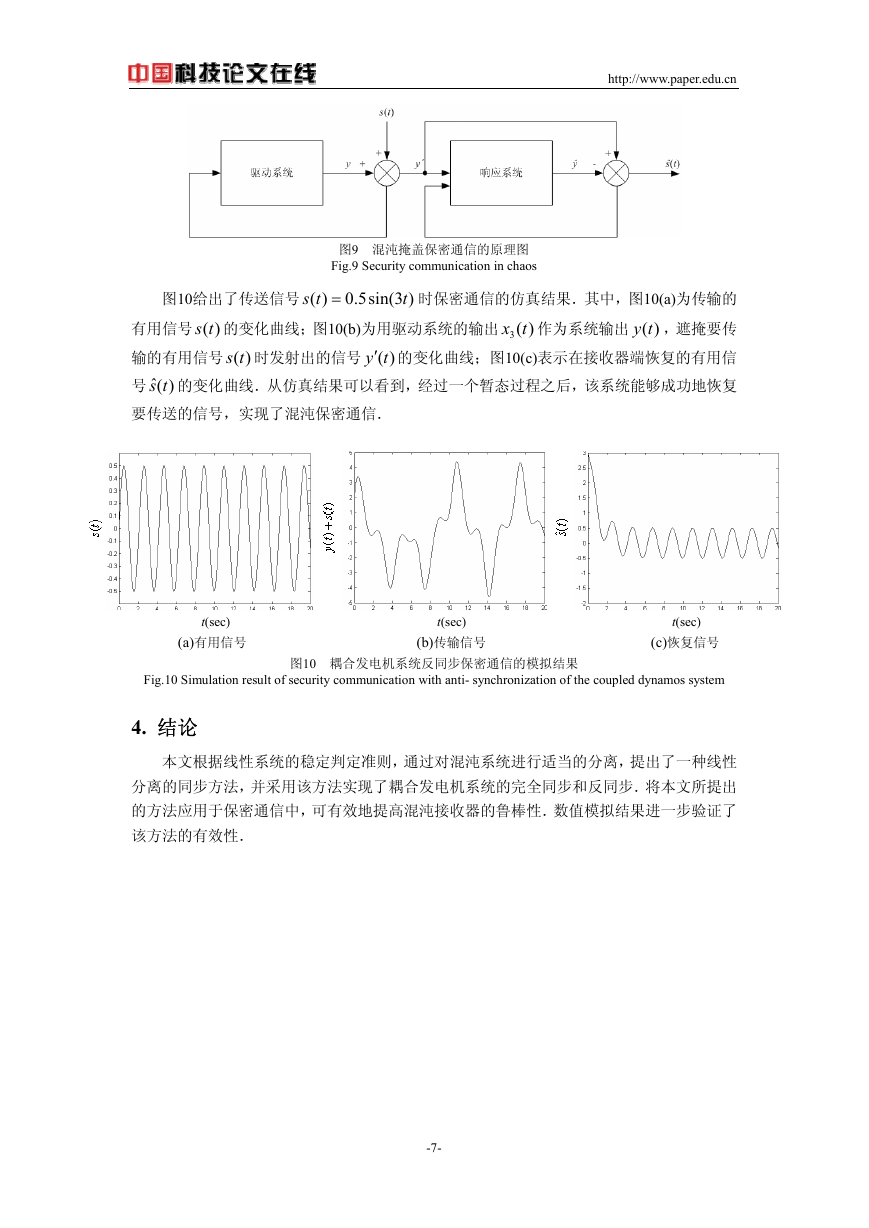利用反同步进行混沌保密通信图9是混沌掩盖保密通信的原理图，通信系统由发送器（即驱动系统）和接收器（即响应系统）组成，运用驱动系统的输出来遮掩要传输的有用信号，被传输的信号是一个要传输的有用信号和混沌信号的混合输出，即被传输的信号和系统的输出同时被发送到接收端．在实际传输的过程中，信道会对传输信号产生各干扰，使系统参数出现畸变，破坏混沌系统的同步．运用前文提出的反同步控制方案，可有效提高混沌接收器的鲁棒性，使接收端恢复被传输信号． -6-

http://www.paper.edu.cn 图9 混沌掩盖保密通信的原理图 Fig.9 Security communication in chaos 图10给出了传送信号 ( ) s t = 0.5sin(3 ) t 时保密通信的仿真结果．其中，图10(a)为传输的有用信号 ( )s t 的变化曲线；图10(b)为用驱动系统的输出 3( ) ，遮掩要传 y t′ 的变化曲线；图10(c)表示在接收器端恢复的有用信输的有用信号号 ˆ( )s t 的变化曲线．从仿真结果可以看到，经过一个暂态过程之后，该系统能够成功地恢复要传送的信号，实现了混沌保密通信． ( )s t 时发射出的信号 ( ) x t 作为系统输出 ( )y t t(sec) t (sec) t(sec) (a)有用信号 (b)传输信号 (c)恢复信号 Fig.10 Simulation result of security communication with anti- synchronization of the coupled dynamos system 图10 耦合发电机系统反同步保密通信的模拟结果 4. 结论本文根据线性系统的稳定判定准则，通过对混沌系统进行适当的分离，提出了一种线性分离的同步方法，并采用该方法实现了耦合发电机系统的完全同步和反同步．将本文所提出的方法应用于保密通信中，可有效地提高混沌接收器的鲁棒性．数值模拟结果进一步验证了该方法的有效性． -7-

http://www.paper.edu.cn 参考文献 [1] Pecora L M, Carroll T L. Synchronization in chaotic systems [J]. Phys Rev Lett, 1990, 64: 821-824 [2] Carroll T L, Pecora L M. Synchronization chaotic circuits [J]. IEEE Trans Circuits Sys, 1991, 38:453-456 [3] 王光瑞，于熙龄，陈式刚．混沌的控制、同步与利用[M]．北京：国防工业出版社，2001，281~455 [4] 关新平，范正平，陈彩莲，等．混沌控制及其在保密通信中的应用[M]．北京：国防工业出版社，2002， 77~255 [5] 王兴元．复杂非线性系统中的混沌[M]．北京：电子工业出版社，2003，91~113 [6] Chen S H, Lü J H. Synchronization of an uncertain unified chaotic system via adaptive control [J]. Chaos, Solitons & Fractals, 2002, 14:643-647. [7] Wang Y W, Guan Z H, Xiao J W. Impulsive control for synchronization of a class of continuous systems [J]. Chaos, 2004, 14: 199-203. [8] Liu F, Ren Y, Shan X M, et al. A linear feedback synchronization theorem for a class of chaotic system [J]. Chaos, Solitons & Fractals, 2002, 13(4): 723~730 [9] Morgul Ö, Solak E. Observer based synchronization of chaotic systems [J]. Physical Review E, 1996, 54(5): 4803~4811 [10] 蒋国平，王锁萍. 细胞神经网络超混沌系统同步及其在保密通信中的应用[J]. 通信学报，2000，21(9)： 79~85 [11] Wang Y W, Guan Z H, Wang H O. LMI-based fuzzy stability and synchronization of Chen's system [J]. Physics Letters A, 2003, 320(2-3): 154~159 [10] Agiza H N, Yassen M T. Synchronization of Rössler and Chen chaotic dynamical systems using active control. Physics Letters A, 2000, 278: 191~197 [11] Liu F, Ren Y, Shan X M, et al. A linear feedback synchronization theorem for a class of chaotic system [J]. Chaos, Solitons & Fractals, 2002, 13(4): 723~730 [12] Morgul Ö, Solak E. On the observer based synchronization of chaotic systems. Physical Review E, 1996, 54(5): 4803~4811 [13] Grassi G, Mascolo S. Nonlinear observer design to synchronize hyperchaotic systems via a scalar signal. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1997, 44(10): 1011~1014 [14] Huijberts H, Lilge T, Nijmeijer H. Nonlinear discrete-time synchronization via extended observers. International Journal of Bifurcation & Chaos, 2001, 11(7):1997~2006 [15] Feki M, Robert B. Observer-based chaotic synchronization in the presence of unknown inputs. Chaos, Solitons & Fractals, 2003, 15(5): 831~840 [16] 王兴元，刘明．用滑模控制方法实现具有扇区非线性输入的主从混沌系统同步[J]．物理学报，2005， 54(6)：118∼123 [17] 王光瑞，于熙龄，陈式刚．混沌的控制、同步与利用[M]．北京：国防工业出版社，2001 [18] 关新平，范正平，陈彩莲，等．混沌控制及其在保密通信中的应用[M]．北京：国防工业出版社，2002 Synchronization and anti-synchronization of a class of chaotic systems and application in security communication School of Electronic & Information Engineering, Dalian University of Technology, Dalian, Wang Xingyuan, Wang Jiagang China (116024 ) Abstract This paper analyses a coupled dynamos system. Based on the stability criterion of linear systems, a new approach for constructing chaotically synchronization and anti-synchronization is proposed. The complete synchronizations and anti-synchronizations of the coupled dynamos system are achieved via the linear separation method. Finally, the method is applied in security communication, and numerical simulations are provided for illustration and verification of the proposed method. Keywords: chaos; synchronization; anti-synchronization; linear separation; coupled dynamos system; chaotic security communication. 作者简介：王兴元，男，1964 年 6 月生，博士，教授，博士生导师，主要研究方向为混沌与分形理论及应用；王甲纲，男，1981 年 10 月生，硕士生，主要研究方向为混沌控制及混沌加密。 -8-

资料库

一类混沌系统的同步、反同步及在保密通信中的应用.pdf

相关推荐

开发技术

热门标签

最新资料