振动力学（刘延柱）课后习题答案.pdf-资料库

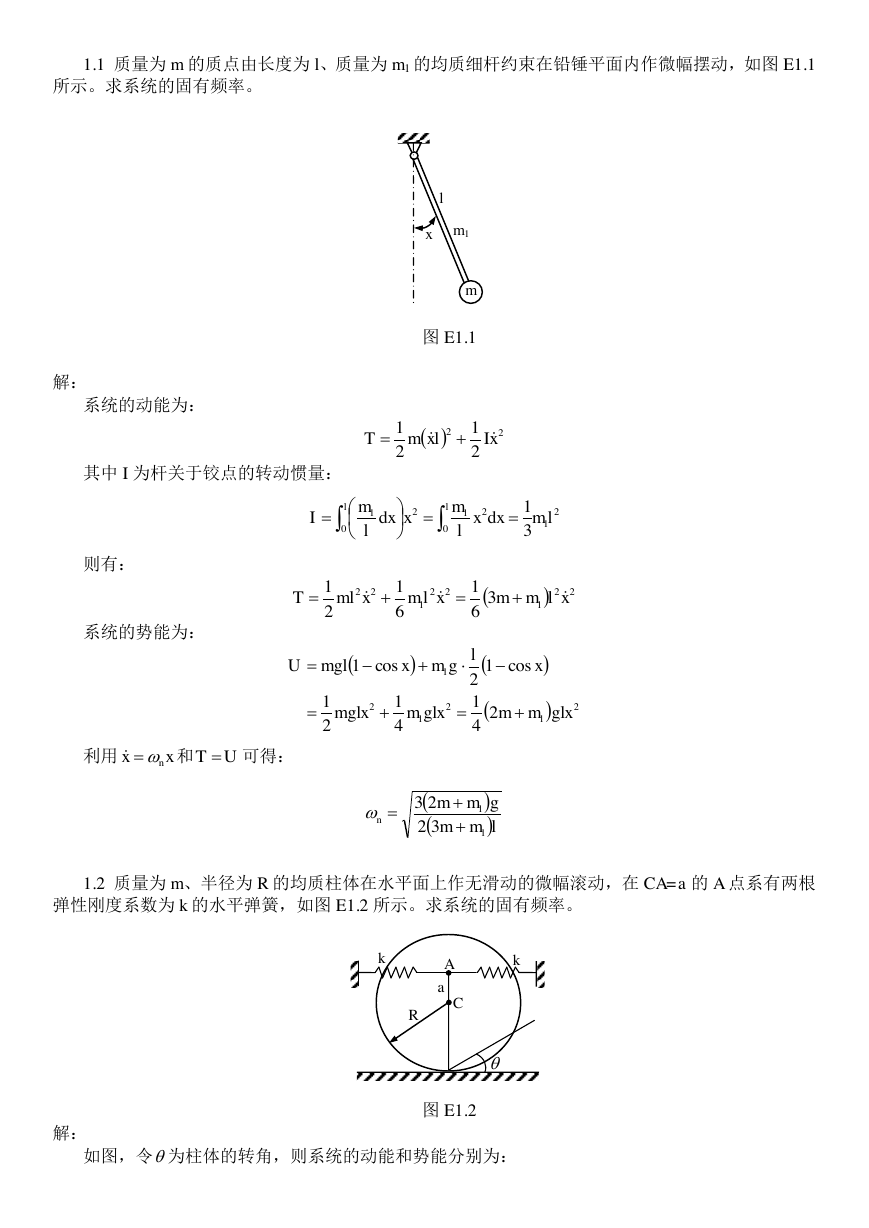
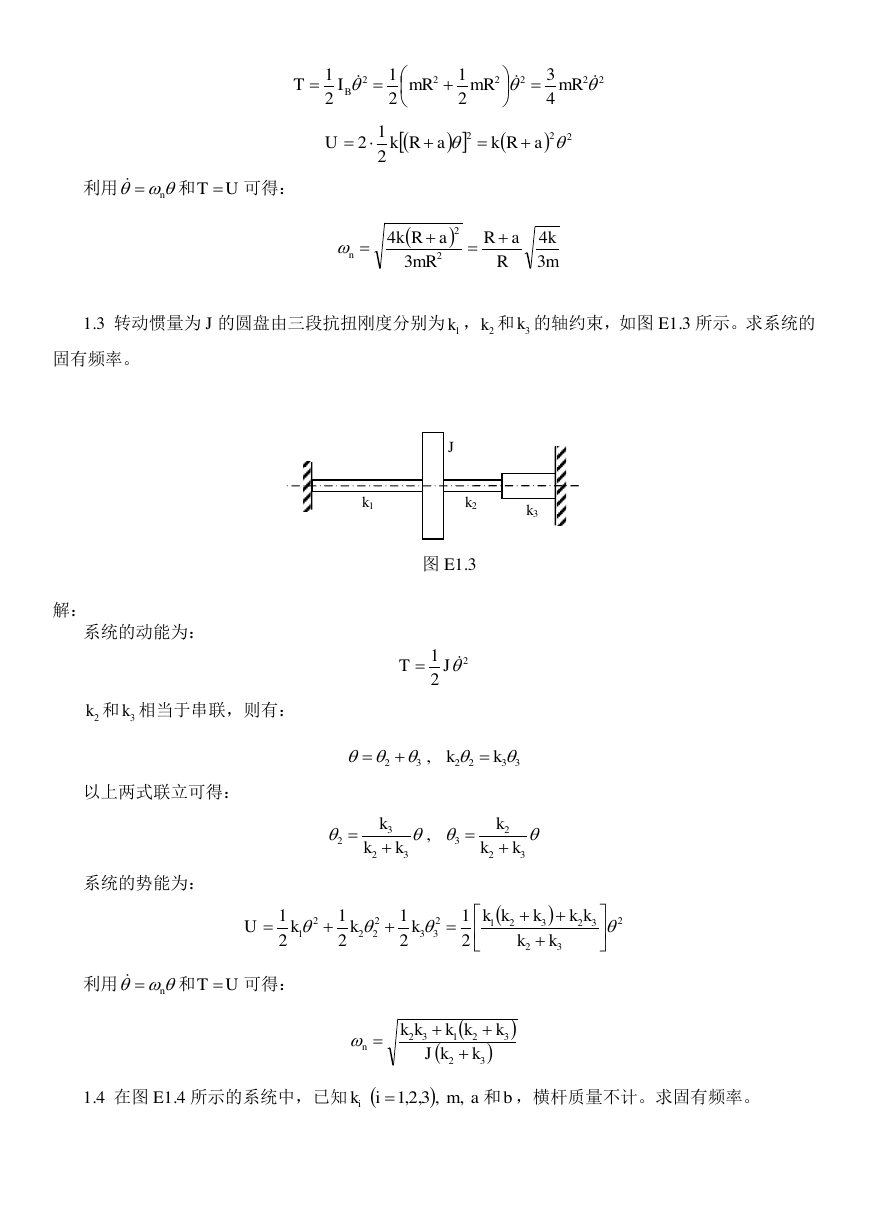
1.1 质量为 m 的质点由长度为 l、质量为 m1 的均质细杆约束在铅锤平面内作微幅摆动，如图 E1.1 所示。求系统的固有频率。解：系统的动能为：其中 I 为杆关于铰点的转动惯量：则有：系统的势能为：利用和可得： l x m1 m 图 E1.1 1.2 质量为 m、半径为 R 的均质柱体在水平面上作无滑动的微幅滚动，在 CA=a 的 A 点系有两根弹性刚度系数为 k 的水平弹簧，如图 E1.2 所示。求系统的固有频率。 k A a C R k 图 E1.2 解：如图，令为柱体的转角，则系统的动能和势能分别为： 222121xIlxmT2102120131lmdxxlmxdxlmIll221221223616121xlmmxlmxmlT2121212414121 cos12cos1glxmmglxmmglxxlgmxmglUxxnUTlmmgmmn113223

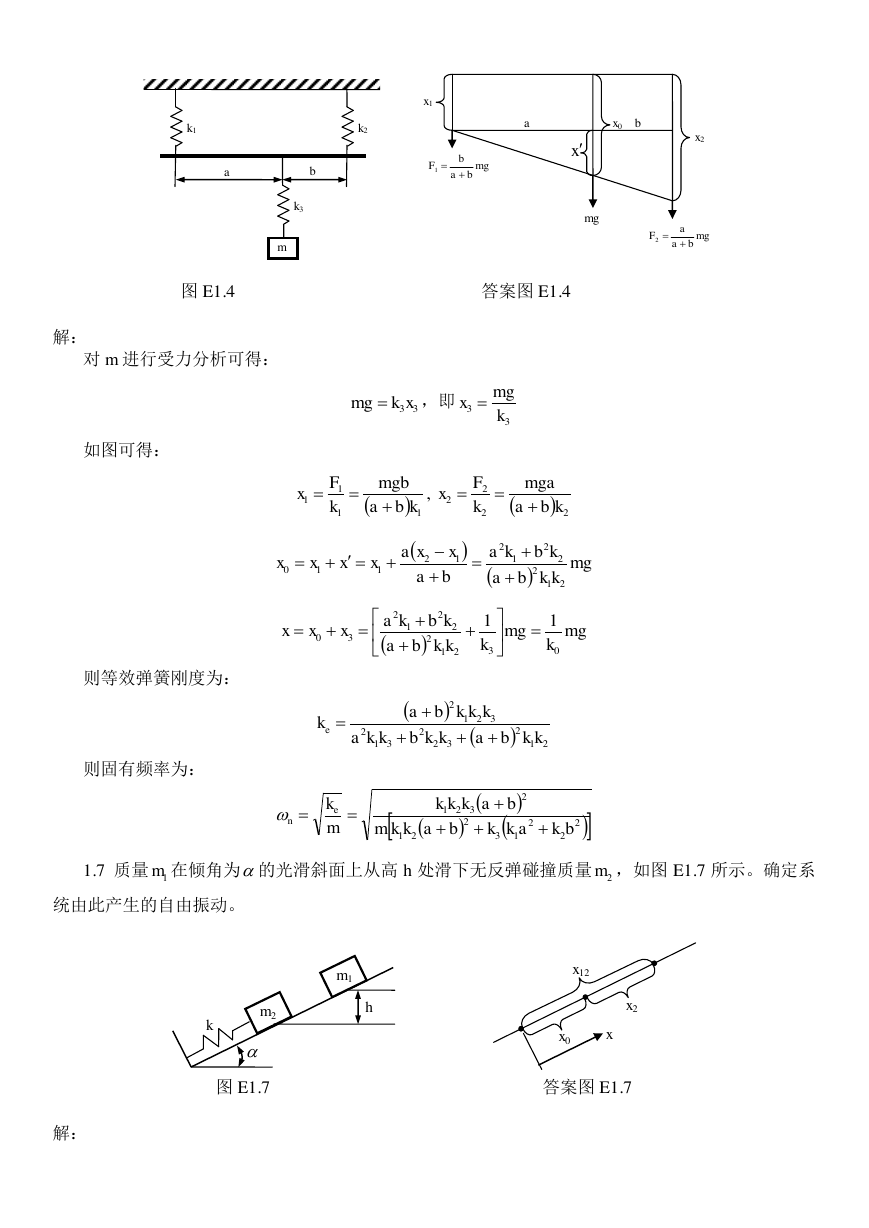
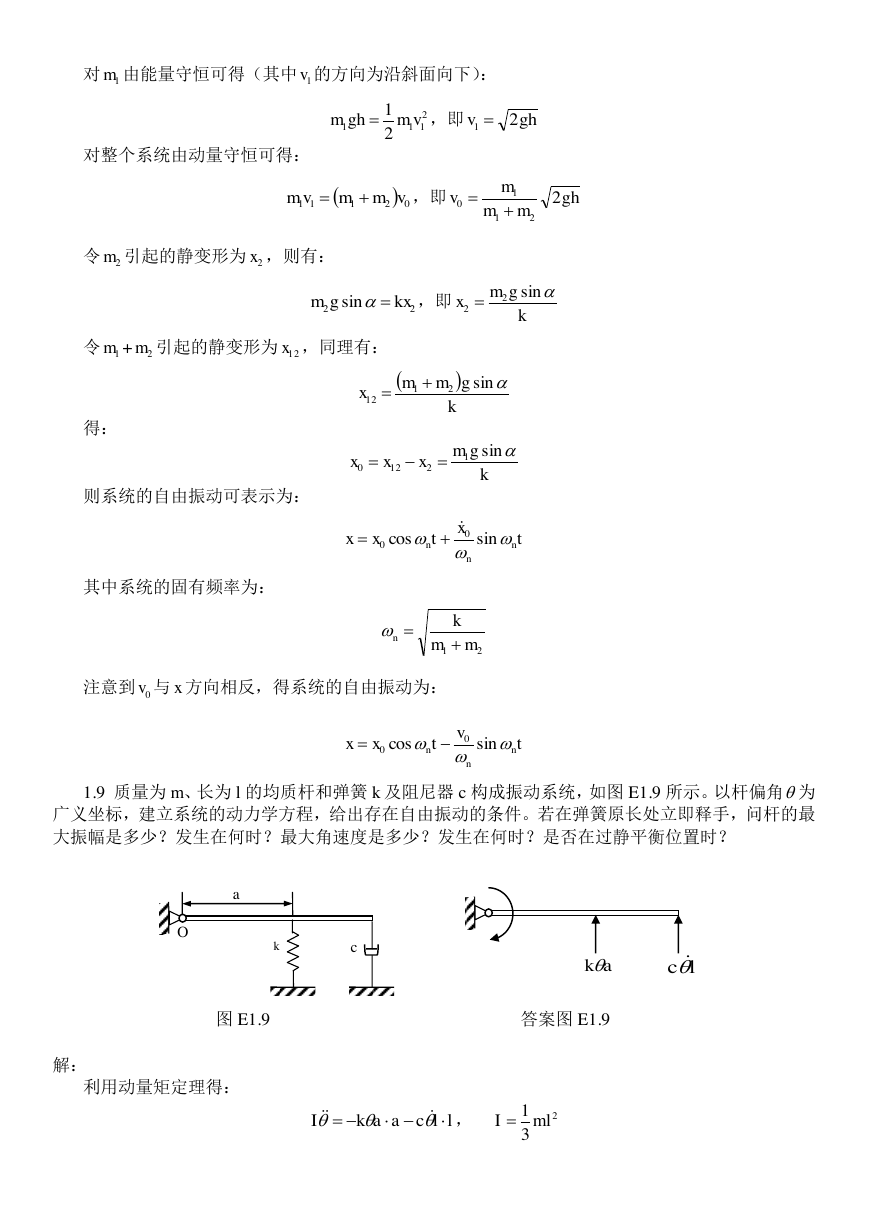
利用和可得： 1.3 转动惯量为 J 的圆盘由三段抗扭刚度分别为，和的轴约束，如图 E1.3 所示。求系统的固有频率。解：系统的动能为：和相当于串联，则有：以上两式联立可得：系统的势能为：利用和可得： J k1 k2 k3 图 E1.3 1.4 在图 E1.4 所示的系统中，已知，横杆质量不计。求固有频率。 22222243212121mRmRmRITB222212aRkaRkUnUTmkRaRmRaRkn3434221k2k3k221JT2k3k332232 , kk32233232 , kkkkkk232323212332222121212121kkkkkkkkkkUnUT3232132kkJkkkkknbamiki , ,3,2,1 和

k1 k2 a b k3 m x1 a x0 b x2 mg 图 E1.4 答案图 E1.4 解：对 m 进行受力分析可得：如图可得：，即则等效弹簧刚度为：则固有频率为： 1.7 质量在倾角为的光滑斜面上从高 h 处滑下无反弹碰撞质量，如图 E1.7 所示。确定系统由此产生的自由振动。 m1 h k m2 x12 x2 x0 x 图 E1.7 答案图 E1.7 解： 33xkmg33kmgx22221111 ,kbamgakFxkbamgbkFxmgkkbakbkabaxxaxxxx212221212110mgkmgkkkbakbkaxxx03212221230112123223123212kkbakkbkkakkkbake222132212321bkakkbakkmbakkkmken1m2mmgbaaF2xmgbabF1

对由能量守恒可得（其中的方向为沿斜面向下）：对整个系统由动量守恒可得：令引起的静变形为，则有：令 + 引起的静变形为，同理有：，即，即，即得：则系统的自由振动可表示为：其中系统的固有频率为：注意到与方向相反，得系统的自由振动为： 1.9 质量为 m、长为 l 的均质杆和弹簧 k 及阻尼器 c 构成振动系统，如图 E1.9 所示。以杆偏角为广义坐标，建立系统的动力学方程，给出存在自由振动的条件。若在弹簧原长处立即释手，问杆的最大振幅是多少？发生在何时？最大角速度是多少？发生在何时？是否在过静平衡位置时？ a O k c 图 E1.9 答案图 E1.9 解：利用动量矩定理得：， 1m1v211121vmghmghv2102111vmmvmghmmmv221102m2x22sinkxgmkgmxsin221m2m12xkgmmxsin2112kgmxxxsin12120txtxxnnnsincos0021mmkn0vxtvtxxnnnsincos00llcaakI231mlIaklc

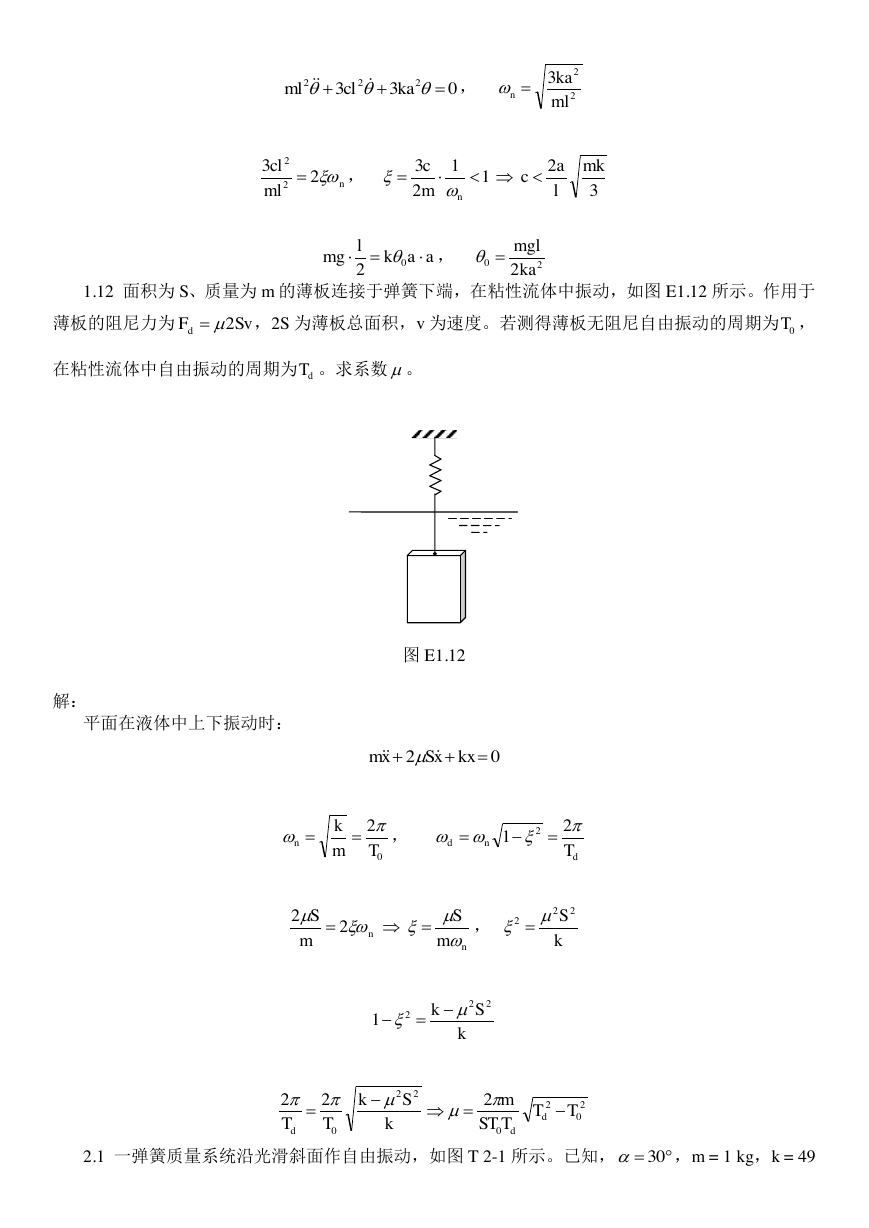
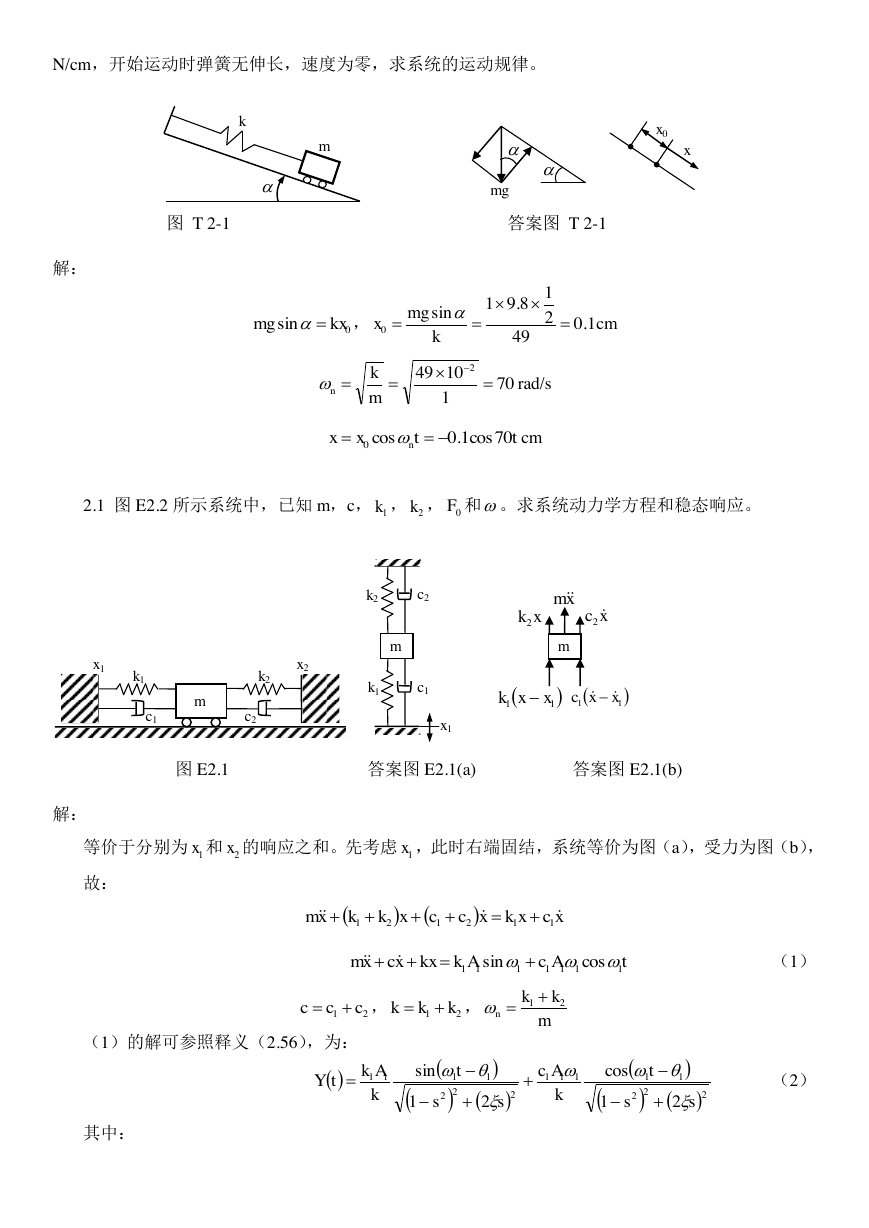
，，， 1.12 面积为 S、质量为 m 的薄板连接于弹簧下端，在粘性流体中振动，如图 E1.12 所示。作用于薄板的阻尼力为，2S 为薄板总面积，v 为速度。若测得薄板无阻尼自由振动的周期为，在粘性流体中自由振动的周期为。求系数。图 E1.12 ，， 2.1 一弹簧质量系统沿光滑斜面作自由振动，如图 T 2-1 所示。已知，，m = 1 kg，k = 49 解：平面在液体中上下振动时： 033222kaclml223mlkannmlcl232232 1123mklacmcnaaklmg02202kamglSvFd20TdT02kxxSxm02TmkndndT212nnmSmS 22kS222kSk22212020220222TTTSTmkSkTTddd30

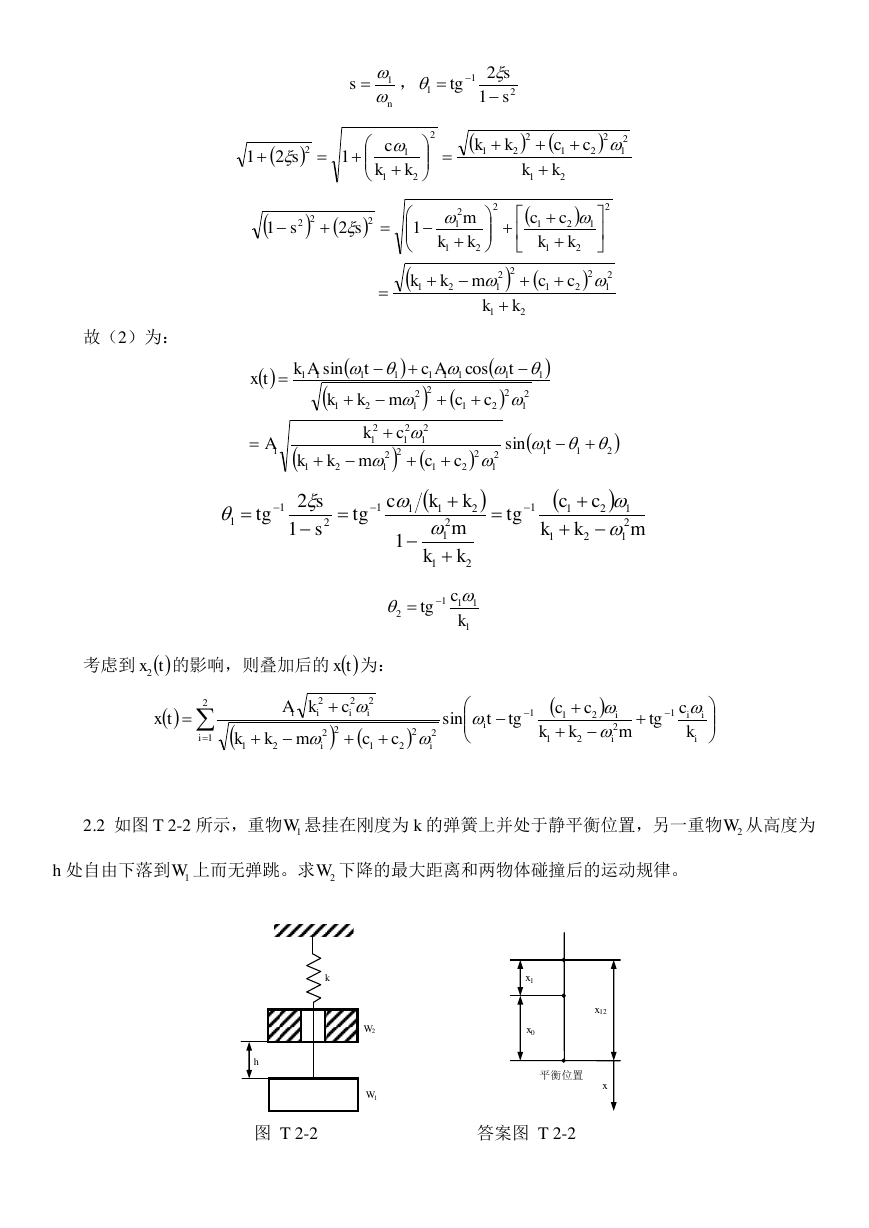
N/cm，开始运动时弹簧无伸长，速度为零，求系统的运动规律。 k m 图 T 2-1 解： mg x0 x 答案图 T 2-1 ， cm rad/s cm 2.1 图 E2.2 所示系统中，已知 m，c，，，和。求系统动力学方程和稳态响应。 x1 k1 x2 k2 m c1 c2 k2 c2 m k1 c1 x1 m 图 E2.1 答案图 E2.1(a) 答案图 E2.1(b) 解：等价于分别为和的响应之和。先考虑，此时右端固结，系统等价为图（a），受力为图（b），故：（1）的解可参照释义（2.56），为：，，其中：（1）（2） 0sinkxmg1.049218.91sin0kmgx70110492mknttxxn70cos1.0cos01k2k0F1x2x1xxcxkxccxkkxm112121tAcAkkxxcxm1111111cossin21ccc21kkkmkkn2122211111222111121cos21sinsstkAcsstkAktYxmxk2xc211xxk11xxc

故（2）为：，考虑到的影响，则叠加后的为： 2.2 如图 T 2-2 所示，重物悬挂在刚度为 k 的弹簧上并处于静平衡位置，另一重物从高度为 h 处自由下落到上而无弹跳。求下降的最大距离和两物体碰撞后的运动规律。 k W2 W1 h x1 x0 x12 平衡位置 x 图 T 2-2 答案图 T 2-2 ns121112sstg212122122122112121kkcckkkkcs21212212212122112122121222 121kkccmkkkkcckkmss211212212212121212112122122121111111111sincossintccmkkckAccmkktActAktxmkkcctgkkmkkctgsstg212112112121211121111211112kctgtx2txiiiiiiiiiiiiikctgmkkcctgtccmkkckAtx12212112122212221222sin1W2W1W2W

解：动量守恒：平衡位置：故：故：，，，， 2.4 在图 E2.4 所示系统中，已知 m，，，和，初始时物块静止且两弹簧均为原长。求物块运动规律。 k1 k2 x1 x2 m m 图 E2.4 答案图 E2.4 解：取坐标轴和，对连接点 A 列平衡方程：即：对 m 列运动微分方程：（1） 222221vgWhWghv22122122vgWWvgWghWWWv22121211kxWkWx111221kxWWkWWx2112kWxxx211202121WWkggWWkntvtxtxtxxnnnnnnsincos sincos120001k2k0F1x2x0sin012211tFxxkxktFxkxkksin0221211222xxkxmtFsin011xk122xxk2xm122xxktFsin0

资料库

振动力学（刘延柱）课后习题答案.pdf

相关推荐

课程资源

热门标签

最新资料