2008年山东海军潜艇学院普通物理考研真题.doc

发布时间：2022-09-15 发布人：admin 分类：说明书资料大小：0.66M 资料格式：doc 举报版权申诉

第1页 / 共9页

第2页 / 共9页

第3页 / 共9页

第4页 / 共9页

第5页 / 共9页

第6页 / 共9页

第7页 / 共9页

第8页 / 共9页

文本预览

2008 年山东海军潜艇学院普通物理考研真题一．单项选择题（本题共 11 小题，每题 3 分，共 33 分，在每小题给出的选项中只有一个是正确的，选对得 3 分，选错、多选或不答均得 0 分） 1．如图 1 所示，一个小物体，位于光滑的水平桌面上，与一绳的一端相连结，绳的另一端穿过桌面中心的小孔 O。该物体原以角速度ω 在半径为 R 的圆周上绕 O 旋转，今将绳从小孔缓慢往下拉，则物体［］。 2．一定量的理想气体贮于某一容器中，温度为 T，气体分子的质量为 m。根据理想气体分子模型和统计假设，分子速度在 x 方向的分量的平均值［］。 3．设有下列过程： (1) 用活塞缓慢地压缩绝热容器中的理想气体。(设活塞与器壁无摩擦) (2) 用缓慢地旋转的叶片使绝热容器中的水温上升。 (3) 一滴墨水在水杯中缓慢弥散开。 (4) 一个不受空气阻力及其它摩擦力作用的单摆的摆动。其中是可逆过程的为［］。 (A) (1)、(2)、(4)。 (B) (1)、(2)、(3)。 (C) (1)、(3)、(4)。 (D) (1)、(4)。 4．有两个相同的容器，容积固定不变，一个盛有氨气，另一个盛有氢气（看成刚性分子的理想气体），它们的压强和温度都相等，现将 5J 的热量传给氢气，使氢气温度升高，如果使氨气也升高同样的温度，则应向氨气传递热量是：［］。 (A) 6 J. (B) 5 J.

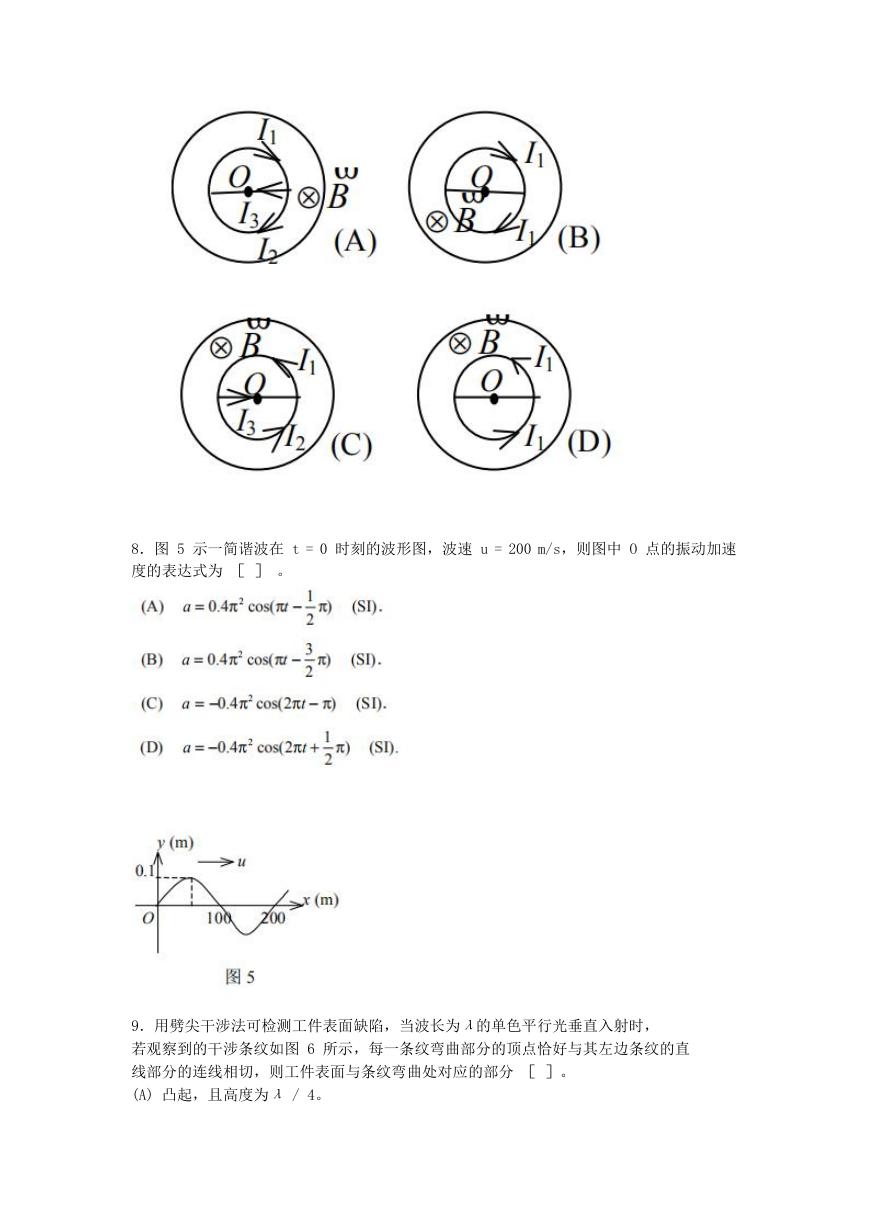
(C) 3 J. (D) 2 J. 5．C1 和 C2 两空气电容器，把它们串联成一电容器组。如图 2 所示。若在 C1 中插入一电介质板，则［］。 6．一矩形线框长为 a 宽为 b，置于均匀磁场中，线框绕 OO′轴，以匀角速度 ω旋转(如图 3 所示)。设 t =0 时，线框平面处于纸面内，则任一时刻感应电动势的大小为［］。 7．用导线围成如图 4 所示的回路(以 O 点为心的圆，加一直径)，放在轴线通过 O 点垂直于图面的圆柱形均匀磁场中，如磁场方向垂直图面向里，其大小随时间减小，则感应电流的流向为［］

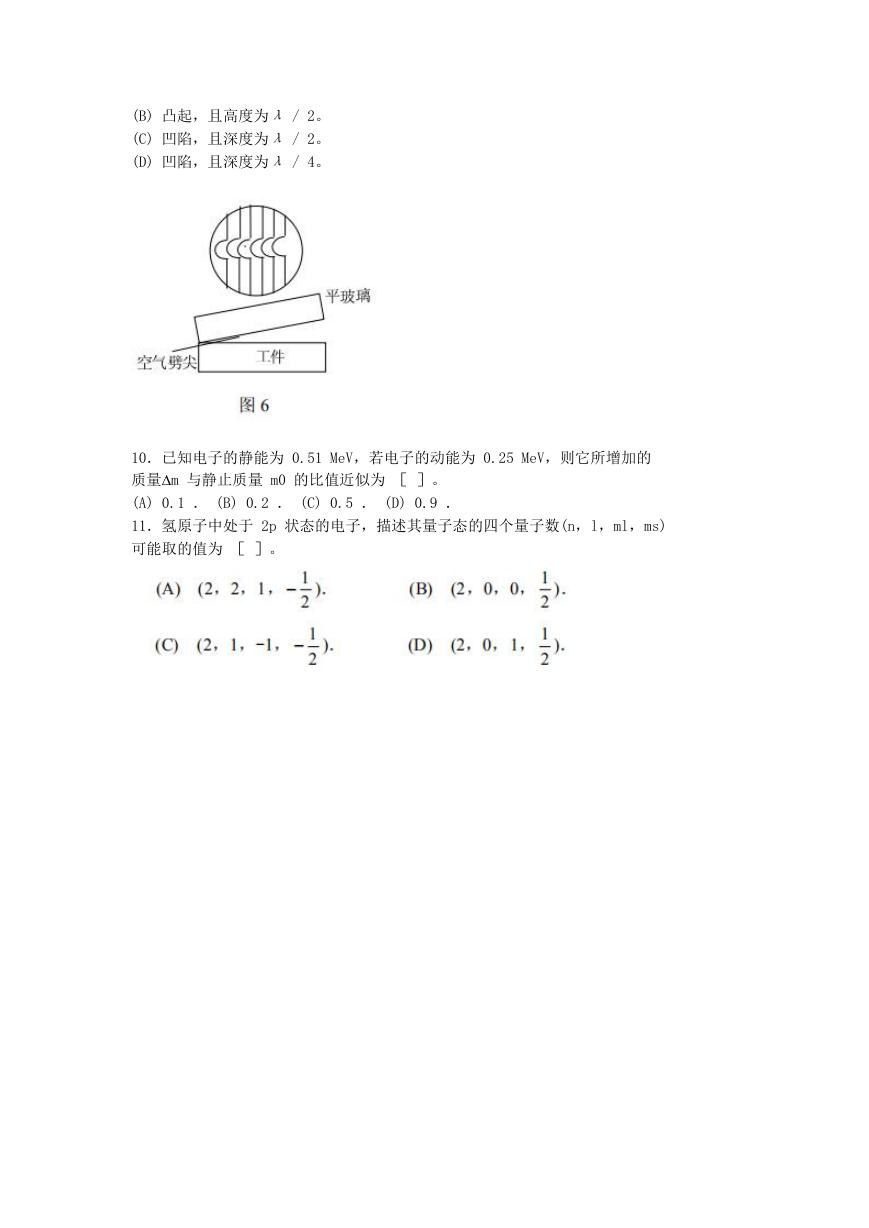
8．图 5 示一简谐波在 t = 0 时刻的波形图，波速 u = 200 m/s，则图中 O 点的振动加速度的表达式为［］。 9．用劈尖干涉法可检测工件表面缺陷，当波长为λ的单色平行光垂直入射时，若观察到的干涉条纹如图 6 所示，每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切，则工件表面与条纹弯曲处对应的部分［］。 (A) 凸起，且高度为λ / 4。

(B) 凸起，且高度为λ / 2。 (C) 凹陷，且深度为λ / 2。 (D) 凹陷，且深度为λ / 4。 10．已知电子的静能为 0.51 MeV，若电子的动能为 0.25 MeV，则它所增加的质量∆m 与静止质量 m0 的比值近似为［］。 (A) 0.1 ． (B) 0.2 ． (C) 0.5 ． (D) 0.9 ． 11．氢原子中处于 2p 状态的电子，描述其量子态的四个量子数(n，l，ml，ms) 可能取的值为［］。

5．在点电荷 q 的电场中，把一个－1.0×10-9 C 的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处，克服电场力作功 1.8×10-5 J，则该点电荷 q ＝_______________。(真空介电常量 0 ε ＝8.85×10-12 C2·N -1·m -2 ) 6．电子在磁感强度 B = 0.1 T 的匀强磁场中沿圆周运动，电子运动形成的等效圆电流强度 I =_______________。 (电子电荷 e =1.60×10-19 C，电子质量 m = 9.11 × 10-31 kg)

12．平行单色光垂直入射在缝宽为 a=0.15 mm 的单缝上。缝后有焦距为 f=400mm 的凸透镜，在其焦平面上放置观察屏幕。现测得屏幕上中央明条纹两侧的两个第三级暗纹之间的距离为 8 mm，则入射光的波长为=_______________。 13．用相互平行的一束自然光和一束线偏振光构成的混合光垂直照射在一偏振片上，以光的传播方向为轴旋转偏振片时，发现透射光强的最大值为最小值的 5 倍，则入射光中，自然光强 I0 与线偏振光强 I 之比为_______________。 14．氢原子由定态 l 跃迁到定态 k 可发射一个光子。已知定态 l 的电离能为 0.85 eV，又知从基态使氢原子激发到定态 k 所需能量为 10.2 eV，则在上述跃迁中氢原子所发射的光子的能量为_______________eV。 15．在电子单缝衍射实验中，若缝宽为 a = 0.1 nm (1 nm = 10-9 m)，电子束垂直射在单缝面上，则衍射的电子横向动量的最小不确定量 y ∆p =_______________N·s。 (普朗克常量 h =6.63×10-34 J·s)

5．一根半径为 R 的长直导线载有电流 I，作一宽为 R、长为 l 的假想平面 S，如图 13 所示。若假想平面 S 可在导线直径与轴 OO＇所确定的平面内离开 OO＇轴移动至远处。试求当通过 S 面的磁通量最大时 S 平面的位置(设直导线内电流分布是均匀的)。

分享到：

赞收藏

资料库

2008年山东海军潜艇学院普通物理考研真题.doc

相关推荐

考研

热门标签

最新资料