论文研究-模块化机器人关节非线性摩擦力建模研究 .pdf-资料库

weixin_39841848-11575855-4744302542940217716.pdf-第1页.png

第1页 / 共7页

weixin_39841848-11575855-4744302542940217716.pdf-第2页.png

第2页 / 共7页

weixin_39841848-11575855-4744302542940217716.pdf-第3页.png

第3页 / 共7页

weixin_39841848-11575855-4744302542940217716.pdf-第4页.png

第4页 / 共7页

weixin_39841848-11575855-4744302542940217716.pdf-第5页.png

第5页 / 共7页

weixin_39841848-11575855-4744302542940217716.pdf-第6页.png

第6页 / 共7页

weixin_39841848-11575855-4744302542940217716.pdf-第7页.png

第7页 / 共7页

中国科技论文在线 http://www.paper.edu.cn 模块化机器人关节非线性摩擦力建模研究 5 10 15 20 唐颖雯1，孙汉旭1，李晓2，宋荆州1** （1. 北京邮电大学自动化学院； 2. 北京航空航天大学机械工程学院）摘要：针对 stribeck 摩擦模型换向时误差较大的问题，提出采用 stribeck 模型+高斯函数的形式来描述模块化机器人关节的摩擦特性，在此基础上进行了参数辨识的实验设计，并通过遗传算法对实际数据进行辨识实验。实验结果表明，采用提出的摩擦模型更能描述模块化关节的摩擦特性。关键词：模块化关节非线性摩擦 stribeck 模型参数辨识中图分类号：TM315 Nonlinear friction modeling for Modular robot joints TANG Yingwen1, SUN Hanxu1, LI Xiao2, SONG Jingzhou1 (1. School of Automation, Beijing University of Posts and Telecommunications; 2. School of Mechanical Engineering and Automation, Beihang University) Abstract: To decrease the effect of error caused by reversing of stribeck model, a new method of Stribeck+Gaussian model was proposed for describing the friction characteristics of Robot’s modular joint. The parameter identification experiment is designed based on this method, and the identification experiment on practical data is carried out through genetic algorithm. The experiment result indicates that it is more appropriate to describe the friction characteristics of modular joint with the friction model which has been proposed. Key words: Modular joint; Nonlinear friction; Stribeck model; Parameter identification 25 0 引言模块化机器人的性能很大程度上由其关节决定，在关节控制中，非线性摩擦力是不容忽视的一环，它对系统的动态和静态性能均有影响，会造成系统爬行、极限环振荡等问题，当系统做低速运动时尤为明显。因此建立一个正确合理、简单有效的摩擦力模型对提高关节的 30 控制性能非常重要。目前已有的摩擦模型可以根据是否由微分方程描述分为静态和动态摩擦模型两类[1]：静态模型中比较常用的有 stribeck 摩擦模型，它具有简单有效，参数易辨识的优点，广泛用于实际应用当中——倪风雷[2]就运用 stribeck 模型建立了谐波驱动的柔性关节的摩擦模型，朱世强[3]在 stribeck 模型的基础上，增加了一个正弦函数项来描述谐波减速器当中与转速有关的摩擦力矩，但 stribeck 模型只能描述匀速时摩擦的静态特性，而且它在零速附近存在不连 35 续，无法描述换向时的摩擦的问题。动态模型既可以描述摩擦的静态特性，也可以描述动态特性，有鬃毛模型、lugre 摩擦模型和 GMS 摩擦模型等；但动态模型能描述的特性越多越精确，模型越复杂，参数也就越多越难辨识，因此综合考虑精确度与模型复杂度，常用 lugre 模型对摩擦力进行建模，具体过程为：首先采用匀速稳态的方式辨识出模型的静态参数，方 40 法同静态摩擦模型的参数一致；接着辨识动态参数，比较常用的方法是对系统预滑动阶段进行研究来辨识系统的动态参数，除此之外，孙宏鑫[4]以控制力为辨识目标，用改进的遗传算法获得动态参数，于伟[5]通过观察电机的自由减速过零现象针对性的讨论 lugre 动态参数的作者简介：唐颖雯(1993-)，女，硕士研究生，主要研究方向:机器人技术通信联系人：孙汉旭(1960-)，男，教授，主要研究方向:机器人技术. E-mail: hxsun@bupt.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 辨识；但总的来说，这些辨识方法都存在实验复杂，对周围环境要求高，辨识过程容易引入干扰等问题。郭彦青[6]对原模型进行离散化，提出了一种可以一次性获得模型所有参数的辨 45 识方法，但此种方法拟合的 lugre 模型在涉及到速度换向时仍有明显滞后误差。在模型的精确性与实用性综合考量后，本文采用 stribeck 模型对模块化关节进行摩擦力建模，同时针对 stribeck 模型难以描述换向时的摩擦这一缺点添加一个高斯项进行补偿，达到降低模型与实际数据之间的误差的效果。 1 包含摩擦力的模块化关节建模 50 1.1 模块化关节的构成本文采用典型的模块化关节结构，关节的驱动系统采用直流无刷伺服电机与单极谐波减速器；内部传感器系统包括集成在电机内部的数字霍尔传感器以及增量式编码器；伺服控制系统由驱动器与控制器构成，其中驱动器可以分别实现电流环、位置环与速度环的 PID 控制，并实时采集电机信息，控制器实现与驱动器的通信、关节内部控制参数调节以及与上位 55 机的通信；制动系统由制动器与继电器开关电路构成。 1.2 包含摩擦力的关节模型对关节进行动力学建模： (1) 式中，为电机输出力矩；为负载折合到电机输出端的力矩；为转动惯量， 60 此处的转动惯量为电机本身和负载折合到电机轴上的转动惯量之和；为电机转速；为关节内部的摩擦力矩。其中为电机转矩系数，可以由厂家提供数据获得，因而在空载状态下，可以通过观 (2) 察电机电流来获得电机当前摩擦力状态。 65 2 非线性摩擦力的建模与参数辨识 2.1 非线性摩擦力模型模块化关节的摩擦力主要来源于轴承摩擦与谐波减速器中刚轮柔轮啮合摩擦，其中谐波减速器的影响最大。用 stribeck 摩擦模型建模如下： (3) 70 其中，为库伦摩擦力；为静摩擦力；为粘性摩擦系数；为 stribeck 速度；然而这个模型在零速附近不连续，一般会采用一个过零点的比例函数来进行补充，但通过实验可以发现，在零速附近的摩擦力动态特性比较明显，主要受到可变静摩擦力和摩擦滞后的影响，只用一个与速度有关的比例函数造成的误差比较大，针对这种情况，本文在零速附近增加了一个与加速度有关的高斯函数来对此时摩擦力的动态 75 特性进行描述，即： - 2 - ωeLfdJTTTdteTLTJωfTemTCimC2ωωωωsfcscvTfffesgnfcfsfvfωsgf

中国科技论文在线 http://www.paper.edu.cn (4) 考虑到函数的连续性，以及速度换向时加速度不同引起的摩擦力的变化，将用下式描述： (5) 80 式中，、、都是需要辨识的参数，为此时电机端的加速度，可以通过电机的速度信息与采样时间信息获得。 2.2 非线性摩擦力参数辨识 2.2.1 实验设计首先进行高增益闭环控制实验，获得相对精确的稳态速度及维持该速度的平均力 85 矩，进而求出摩擦力的静态参数、、和。此时 (6) (7) 具体的实验步骤为：1.将电机的期望速度设为 1rpm，以 0.5rpm 的间隔递增一直增加到 10rpm；2.以 2rpm 的间隔递增，运行到 50rpm；记录在每一速度下，电机正反方 90 向的转速与电流的平均值，一共获得 80 组数据，对所得电流值除以转矩系数即可得到摩擦力矩。接着在求出 stribeck 摩擦模型系数的基础下，进行第二个加速度的实验：让电机以不同的加速度进行匀变速运动，记录下这个过程当中电机转速与电流值，按照一定间 95 隔时间对电机的转速与电流进行采样并取平均值，具体实验步骤为：将初始速度设置为 50rpm 或-50rpm，从 0.1rad/s2 开始，以 0.1rad/ s2 的间隔增加加速度，分别进行加速和减速两个实验，一直到 1.5rad/ s2。 2.2.2 数据处理获得实验数据后，采用遗传算法对数据进行拟合，摩擦力矩的误差定义为： (8) 100 为实际测得的力矩，为识别的力矩，目标函数定义为： (9) 根据实验 1 所得数据，静摩擦系数辨识结果如图： - 3 - 2ωωωωsfcscvgTfffesgnffgf2ωv*ω**a*ω***gscsfsessgnfflvadsgnacsgnldcacfsfvfωsω0LdTdtefmTTCiˆeffTTfTˆfT21ˆJNfifiITT

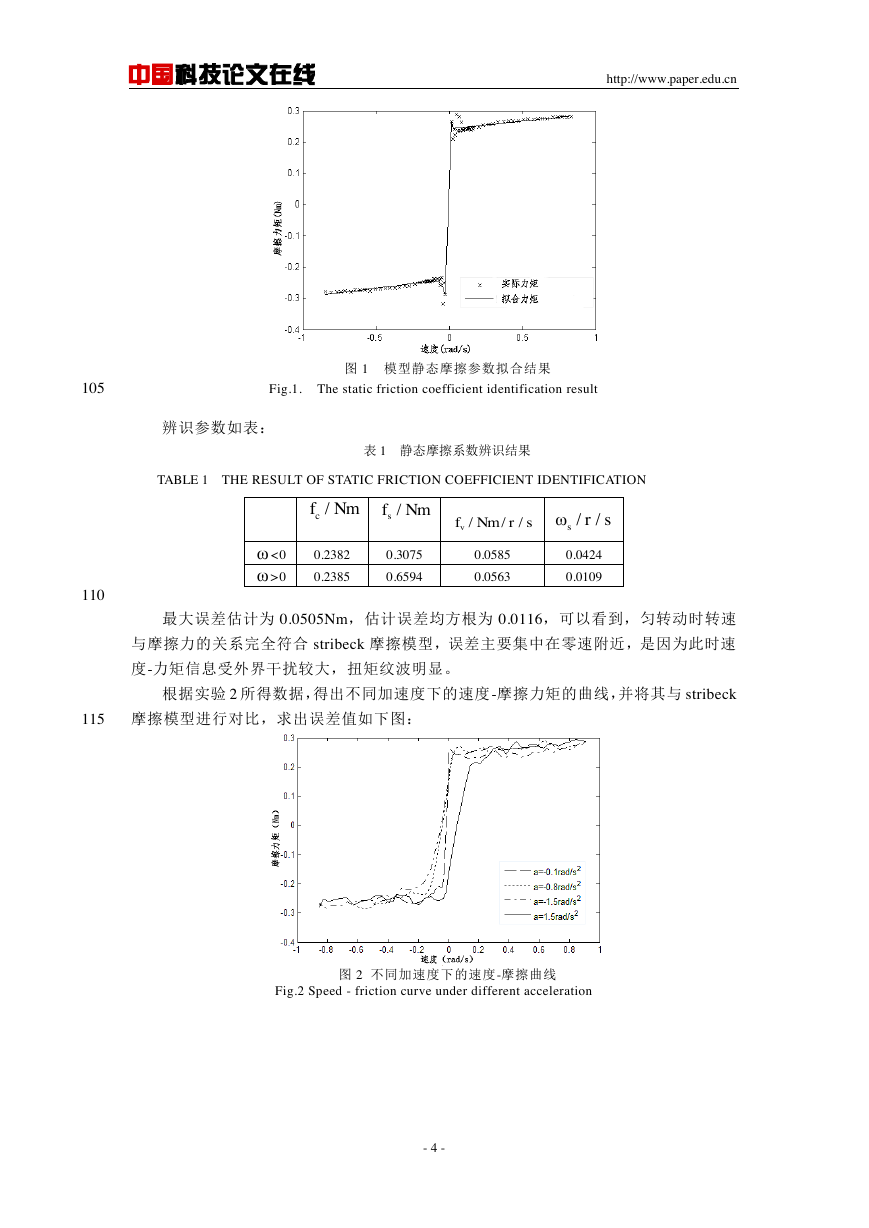
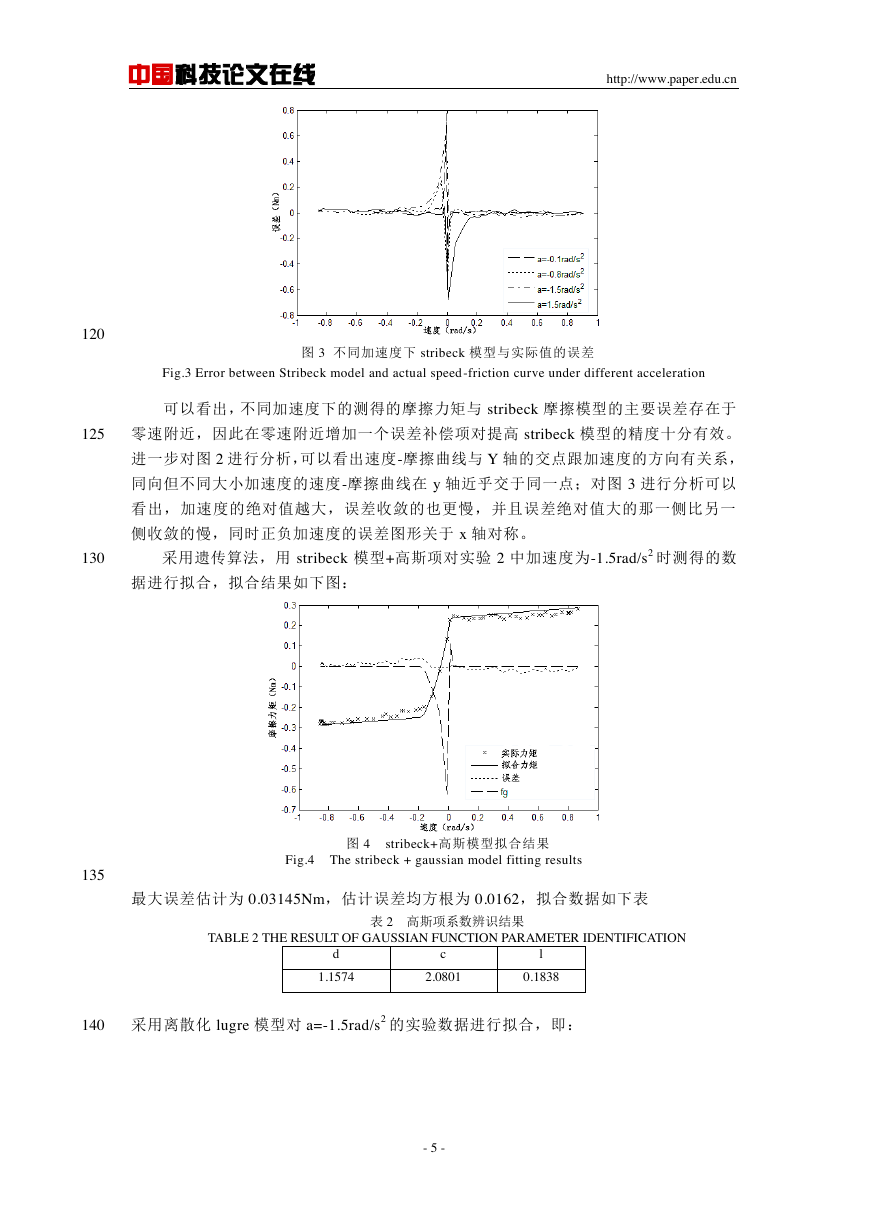
中国科技论文在线 http://www.paper.edu.cn 图 1 模型静态摩擦参数拟合结果 105 Fig.1. The static friction coefficient identification result 辨识参数如表：表 1 静态摩擦系数辨识结果 TABLE 1 THE RESULT OF STATIC FRICTION COEFFICIENT IDENTIFICATION <0 >0 0.2382 0.3075 0.2385 0.6594 0.0585 0.0563 0.0424 0.0109 110 最大误差估计为 0.0505Nm，估计误差均方根为 0.0116，可以看到，匀转动时转速与摩擦力的关系完全符合 stribeck 摩擦模型，误差主要集中在零速附近，是因为此时速度-力矩信息受外界干扰较大，扭矩纹波明显。根据实验 2 所得数据，得出不同加速度下的速度-摩擦力矩的曲线，并将其与 stribeck 115 摩擦模型进行对比，求出误差值如下图：图 2 不同加速度下的速度-摩擦曲线 Fig.2 Speed - friction curve under different acceleration - 4 - /cfNm/sfNm///vNmrfsω//srsωω

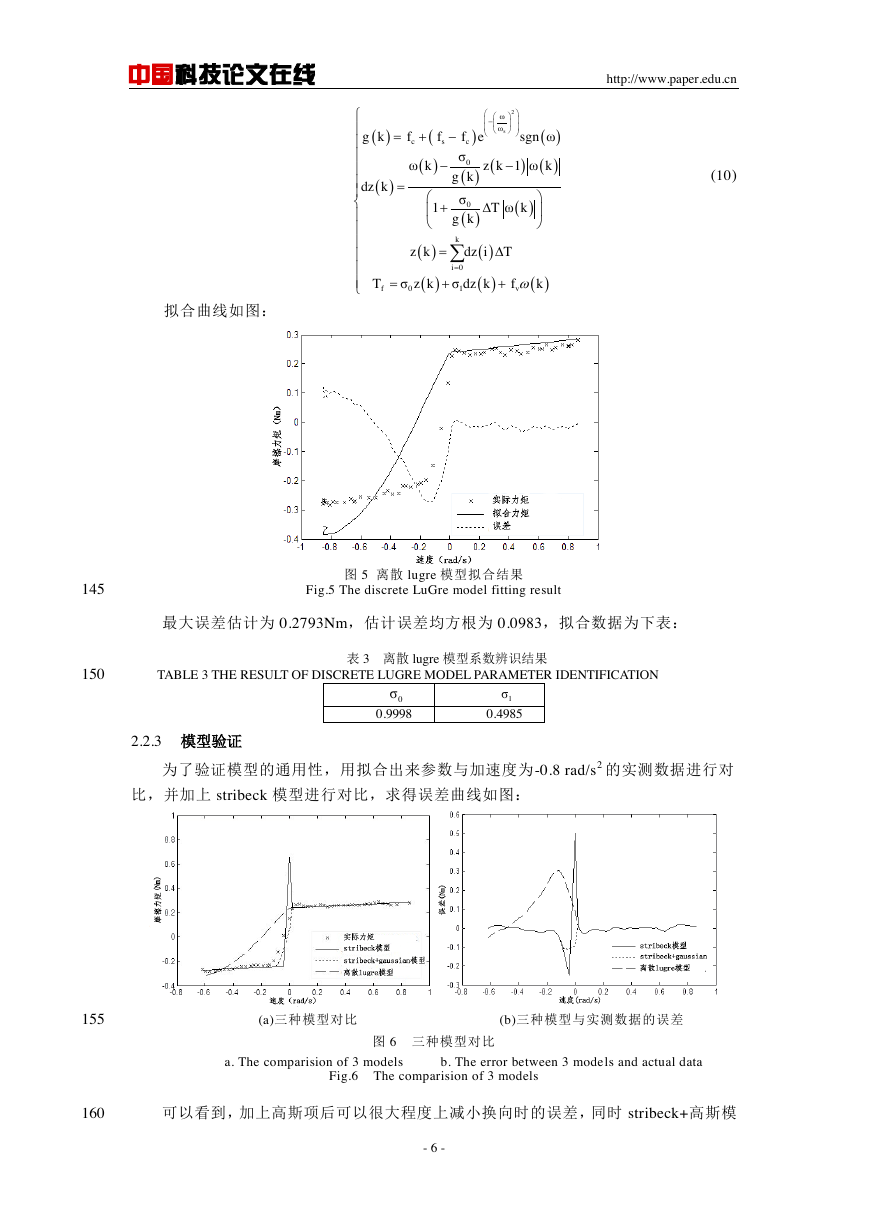
中国科技论文在线 http://www.paper.edu.cn 120 图 3 不同加速度下 stribeck 模型与实际值的误差 Fig.3 Error between Stribeck model and actual speed -friction curve under different acceleration 可以看出，不同加速度下的测得的摩擦力矩与 stribeck 摩擦模型的主要误差存在于 125 零速附近，因此在零速附近增加一个误差补偿项对提高 stribeck 模型的精度十分有效。进一步对图 2 进行分析，可以看出速度-摩擦曲线与 Y 轴的交点跟加速度的方向有关系，同向但不同大小加速度的速度-摩擦曲线在 y 轴近乎交于同一点；对图 3 进行分析可以看出，加速度的绝对值越大，误差收敛的也更慢，并且误差绝对值大的那一侧比另一侧收敛的慢，同时正负加速度的误差图形关于 x 轴对称。 130 采用遗传算法，用 stribeck 模型+高斯项对实验 2 中加速度为-1.5rad/s2 时测得的数据进行拟合，拟合结果如下图：图 4 stribeck+高斯模型拟合结果 Fig.4 The stribeck + gaussian model fitting results 135 最大误差估计为 0.03145Nm，估计误差均方根为 0.0162，拟合数据如下表 TABLE 2 THE RESULT OF GAUSSIAN FUNCTION PARAMETER IDENTIFICATION 表 2 高斯项系数辨识结果 d 1.1574 c l 2.0801 0.1838 采用离散化 lugre 模型对 a=-1.5rad/s2 的实验数据进行拟合，即： 140 - 5 -

中国科技论文在线 http://www.paper.edu.cn (10) 拟合曲线如图： 145 图 5 离散 lugre 模型拟合结果 Fig.5 The discrete LuGre model fitting result 最大误差估计为 0.2793Nm，估计误差均方根为 0.0983，拟合数据为下表：表 3 离散 lugre 模型系数辨识结果 150 TABLE 3 THE RESULT OF DISCRETE LUGRE MODEL PARAMETER IDENTIFICATION 0.9998 0.4985 2.2.3 模型验证为了验证模型的通用性，用拟合出来参数与加速度为 -0.8 rad/s2 的实测数据进行对比，并加上 stribeck 模型进行对比，求得误差曲线如图： 155 (a)三种模型对比 (b)三种模型与实测数据的误差 a. The comparision of 3 models b. The error between 3 mode ls and actual data 图 6 三种模型对比 Fig.6 The comparision of 3 models 160 可以看到，加上高斯项后可以很大程度上减小换向时的误差，同时 stribeck+高斯模 - 6 - 2ωω00001kωσωk1ωkkσ1ωkkσσscsckifvgfffesgnzkgkdzTgkzdziTTzkdzkfk0σ1σ

中国科技论文在线 http://www.paper.edu.cn 型具有运算简单快速，参数辨识实验设计方便、容易实现的优点。 3 结论针对 stribeck 模型无法描述换向时的非线性摩擦力的问题，提出了一种 stribeck 模型+ 高斯函数的新的形式来描述模块化关节的摩擦特性，并根据模型设计了参数辨识实验，实验 165 证明采用提出的新模型可以更好的描述换向时的非线性摩擦力，同时参数辨识实验简单有效，为之后的模块化关节的摩擦建模提供了实验参考。 [参考文献] (References) 170 175 [1] 刘丽兰,刘宏昭,吴子英,王忠民.机械系统中摩擦模型的研究进展[J].力学进展，2008，38（2）：201-213 [2] 倪风雷，刘业超，黄剑斌.具有谐波减速器柔性关节摩擦力辨识及控制[J].机械与电子，2012（4）:71-74 [3] 朱世强，吴文祥，王宣银，刘华山.考虑摩擦的谐波驱动机器人低速运动控制方法[J].农业机械学报， 2013,44(11):293-299 [4] 孙洪鑫，王修勇，陈政清 . 基于改进遗传算法的 LuGre 模型参数辨识 [J]. 武汉理工大学学报， 2009,31(23):113-117. [5] 于伟，马佳光，李锦英，肖靖.基于 LuGre 模型实现精密伺服转台摩擦参数辨识及补偿[J].光学精密工程， 2011,19(11)：2736-2743. [6] 郭彦青，付永领，张朋.一种新型 LuGre 摩擦模型参数辨识方法[J].机床与液压，2015(1)：149-152. - 7 -

资料库

论文研究-模块化机器人关节非线性摩擦力建模研究 .pdf

相关推荐

开发技术

热门标签

最新资料