无线通信答案goldsmith.pdf-资料库

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第1页.png

第1页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第2页.png

第2页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第3页.png

第3页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第4页.png

第4页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第5页.png

第5页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第6页.png

第6页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第7页.png

第7页 / 共86页

c35c9b7e-9c5e-495d-ab8d-f50b14539c5f.pdf-第8页.png

第8页 / 共86页

Chapter 1 1. In case of an accident, there is a high chance of getting lost. The transportation cost is very high each time. However, if the infrastructure is set once, it will be very easy to use it repeatedly. Time for wireless transmission is negligible as signals travel at the speed of light. 2. Advantages of bursty data communication (a) Pulses are made very narrow, so multipaths are resolvable (b) The transmission device needs to be switched on for less time. Disadvantages (a) Bandwidth required is very high (b) Peak transmit power can be very high. 3. Pb = 10−12 2γ = 10−12 γ = 1012 1 2 = 5 × 1011 (very high) 4. Geo: 35,786 Km above earth ⇒ RT T = 2×35786×103 = 0.2386s Meo: 8,000- 20,000 Km above earth ⇒ RT T = 2×8000×103 Leo: 500- 2,000 Km above earth ⇒ RT T = 2×500×103 Only Leo satellites as delay = 3.3ms < 30ms c c c = 0.0033s = 0.0533s 5. 6. optimum no. of data user = d optimum no. of voice user = v Three diﬀerent cases: Case 1: d=0, v=6 ⇒ revenue = 60.80.2 = 0.96 Case 2: d=1, v=3 revenue = [prob. of having one data user]×(revenue of having one data user) + [prob. of having two data user]×(revenue of having two data user) + [prob. of having one voice user]×(revenue of having one voice user) + [prob. of having two voice user]×(revenue of having two voice user) + [prob. of having three or more voice user]×(revenue in this case) ⇒ 0.52 × $1 + 0.52 × $1 + 0.8 × 0.25 × $0.2 + 0.82 × 0.24 × $0.4+ 0.8 × 0.25 × $0.2 − 0.82 × 0.24 × $0.4 × $0.6 2 1 1 − 6 1 6 2 6 1 6 2 ⇒ $1.35 Case 3: d=2, v=0 revenue =2 × 0.5 = $1 So the best case is case 2, which is to allocate 60kHz to data and 60kHz to voice.

7. 8. 1. Hand-oﬀ becomes a big problem. 2. Inter-cell interference is very high and should be mitigated to get reasonable SINR. 3. Infrastructure cost is another problem. 9. Smaller the reuse distance, larger the number of users who can use the same system resource and so 10. capacity (data rate per unit bandwidth) increases. (a) 100 cells, 100 users/cell ⇒ 10,000 users (b) 100 users/cell ⇒ 2500 cells required 100km2 Area/cell = 2500cells ⇒ Area cell = .04km2 (c) From Rappaport or iteration of formula, we get that 100 channels cell ⇒ 89 channels cell @Pb = .02 Each subscriber generates 1 Thus, each cell can support 30 × 89 = 2670 subscribers Macrocell: 2670 × 100 ⇒ 267, 000 subscribers Microcell: 6,675,000 subscribers 30 of an Erlang of traﬃc. (d) Macrocell: $50 M Microcell: $1.25 B (e) Macrocell: $13.35 M/month ⇒ 3.75 months approx 4 months to recoop Microcell: $333.75 M/month ⇒ 3.75 months approx 4 months to recoop 11. One CDPD line : 19.2Kbps average Wimax ∼ 40M bps ∴ number of CDPD lines ∼ 2 × 103

1. (a) Chapter 10 (AAH)T = (AH)T .AT = (AT )T = AAH ∴ (AAH)H = AAH AT For AAH , λ = λ, i.e. eigen-values are real AAH = QΛQH (b) X H AAH X = (X H A)(X H A)H = X H A ≥ 0 ∴ AAH is positive semideﬁnite. (c) IM + AAH = IM + QΛQH = Q(I + Λ)QH AH positive semideﬁnite ⇒ λi ≥ 0∀i ∴ 1 + λi > 0∀i ∴ IM + AAH positive deﬁnite (d) det[IM + AAH] = det[IM + QΛQH] = det[Q(IM + ΛM )QH] = det[IM + ΛM ] = ΠRank(A) (1 + λi) i=1 det[IN + AH A] = det[IN + QΛQH] = det[Q(IN + ΛN )QH] = det[IN + ΛN ] = ΠRank(A) (1 + λi) i=1 ∵ AAH and AH A have the same eigen-value ∴ det[IM + AAH] = det[IN + AH A] 2. H = UΣV T U =  −0.4793  1.7034 Σ = 0.8685 −0.1298 −0.5896 −0.4272 −0.6855 −0.6508 −0.2513 0.7164 0 0 0.7152 0 0 0 0 0.1302  

V =  −0.3458  V =  1 0 0 1 0 0 ∴ H =  0.6849 0.4263 −0.5708 0.2191 0.0708 −0.7116 −0.6109 0.0145 −0.2198 0.3311 −0.9017 1 0 0 2  1 0  1 0 0  Σ =  0 1 0 0 0 2 0 0 0 0 3. H = UΣV T Let U = 4. Check the rank of each matrix rank(HI) = 3 ∴ multiplexing gain = 3 rank(H2) = 4 ∴ multiplexing gain = 4 5. 6. Vi = ρ Constraint λi = constant RH i=1 log2 C = 1 + λiρ Mt ∴ ∂C ∂λi = ρ 1 Mt ln 2 (1 + λiρ Mt ) − ρ Mt ln 2 1 (1 + λiρ Mt ) = 0 ⇒ λi = λj ∴ when all RH singular values are equal, this capacity is maximized. (a) Any method to show H ≈ UΛV is acceptable. For example: Hij−H Hij × 100 (b) precoding ﬁlter M = V −1 D = .05 .09 .14 .23 .13 .10 .13 .08 .11  where : dij =  −.5195 −.3460 −.7813  −.2407 −.8894 shaping ﬁlter F = U−1 −.0251 −.9078 .4188 −.8540 .2373 .4629 .3887 −.4727 −.2423 −.8473 −.8478 .3622 .3876 M = F = (c) Pi Thus Y = F(H)MX + FN = U∗UΛVV ∗X + U∗N = ΛX + U∗N − 1 P = 1 γo 2P γi = λi NoB = 94.5 for i = 1, 6.86 for i = 2, .68 for i = 3 Assume γ2 > γ0 > γ3 since γ3 = .68 is clearly too small for data transmission , 0 else for 1 γi > 1 γo γi

Pi − 1 γ2 − 1 P = 1 ⇒ 2 γ0 P = .5676 P2 P = .4324 P1 C = B 1 + γ1 log2 P1 P = 775.9 kbps γ1 = 1 ⇒ γ0 = 1.73 + log2 1 + γ2 P2 P (d) With equal weight beamforming, the beamforming vector is given by c = 1√ is then given by: SN R = cH H H Hc N0B = (.78)(100) = 78. (3) [1 1 1]. The SNR (1) This gives a capacity of 630.35 kbps. The SNR achieved with beamforming is smaller than the best channel in part (c). If we had chosen c to equal the eigenvector corresponding to the best eigenvalue, then the SNR with beamforming would be equal to the largest SNR in part(c). The beamforming SNR for the given c is greater than the two smallest eigenvalues in part(c) because the channel matrix has one large eigenvalue and two very small eigenvalues. 7. C = max B log2 det[IM γ + HRX H H] RX : Tγ(RX) = ρ If the channel is known to the transmitter, it will perform an SVD decomposition of H as H = UΣV HRX H H = (UΣV )RX(UΣV )H By Hadamard’s inequality we have that for A ∈ n×n det(A) ≤ Πn i=1Aii with equality iﬀ A is diagonal. We choose RX to be diagonal, say = Ω then det(IM R + HRX H H) = det(I + ΩΣ2) ∴ C = max i ρi≤ρ Bσi log2(1 + λiρi) √ λi are the singular values. where 8. The capacity of the channel is found by the decomposition of the channel into RH parallel channels, where RH is the rank of the channel matric H. √ λi are the RH non-zero singular values of the channel matrix H and ρ is the SNR constraint. where C = max i ρi≤ρ ρi: i B log2(1 + λiρi) γi = λiρ 1 γ0 0 C = B log2(γi/γ0) i:γi≥γ0 Then the optimal power allocation is given as Pi P = − 1 γi γi ≥ γ0 γi < γ0 (2) for some cut-oﬀ value γ0. The resulting capacity is given as

For H = RH = 3, γ1 = 80, γ2 = 40, γ3 = 40. We ﬁrst assume that γ0 is less than the minimum γi which is 40.  1 1 1 −1 −1 1 1 1 1 1 −1 1 1  1 1 −1 3 3 1 + 1 γi i=1 γ0 = C B = 12.4732 bits/sec/Hz  1 1 −1 1 1 −1 1 1 1 −1 1 1 1 −1 −1 −1  which gives γ0 = 2.8236 < mini γi, hence the assumption was correct. For H = RH = 4, γ1 = 40, γ2 = 40, γ3 = 40, γ4 = 40. We ﬁrst assume that γ0 is less than the minimum γi which is 40. 4 4 γ0 = 1 + 1 γi i=1 which gives γ0 = 3.6780 < mini γi, hence the assumption was correct.  h11 . . . hMr1 9. H = C B = 13.7720 bits/sec/Hz  Mr×Mt h1Mt . . . . . . . . . . . . . . . hMrMt . . .

Denote G = HH T lim Mt→∞ 1 Mt Gii = lim Mt→∞ 1 Mt = lim Mt→∞ 1 Mt = Ejhij2 = σ2 = 1 ∀i lim Mt→∞,i=j 1 Mt Gij = lim Mt→∞ 1 Mt     hi1 . . . hiMt hj1 . . . hjMt [hi1 . . . hiMt] Mt j=1 hij2 [hi1 . . . 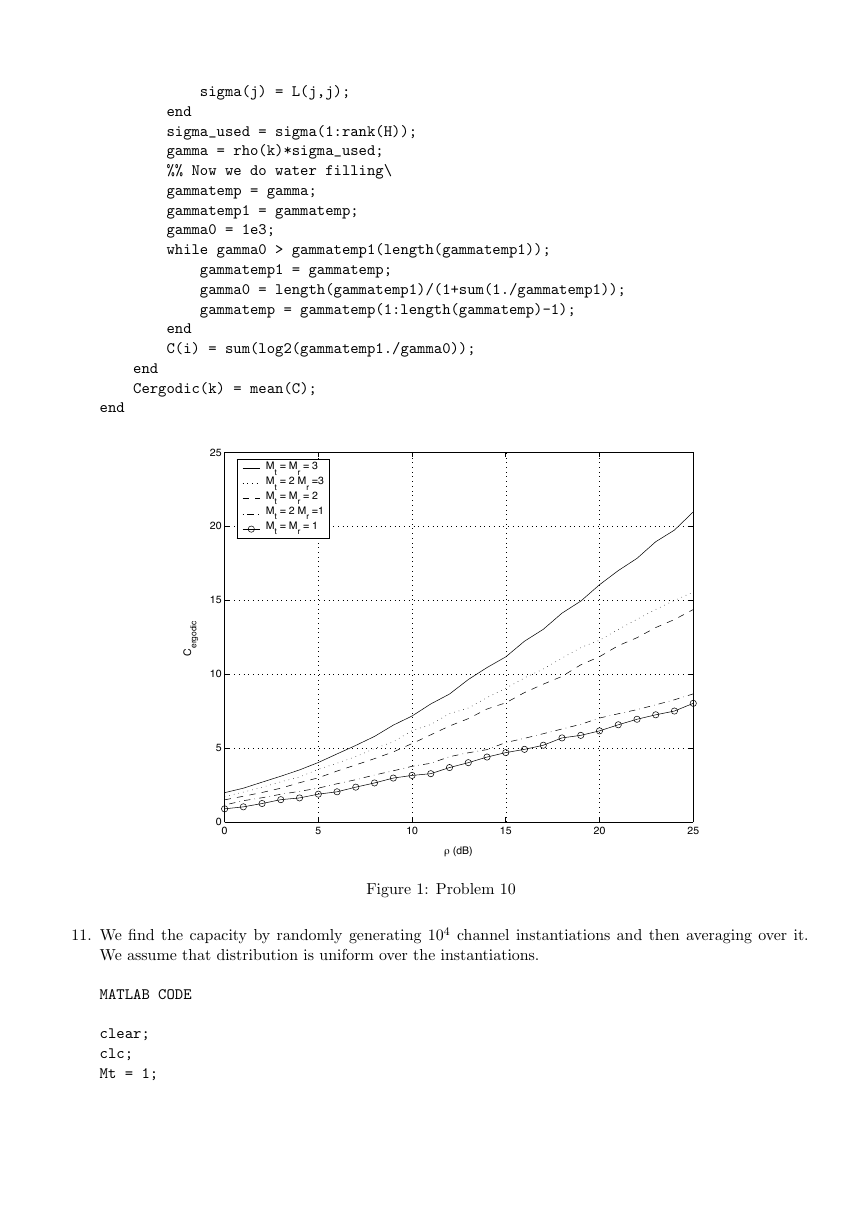hiMt] Mt hikhjk 1 ∴ lim M→∞ M IM + ρ M HH T HH T = IM ∴ lim M→∞ B log2 det k=1 = lim Mt→∞ 1 Mt = Ekhikhjk = Ek(hik)Ek(hjk) = 0 ∀i, j, i = j = B log2 det [IM + ρIM ] = B log2 [1 + ρ] det IM = M B log2 [1 + ρ] 10. We ﬁnd the capacity by randomly generating 103 channel instantiations and then averaging over it. We assume that distribution is uniform over the instantiations. MATLAB CODE clear; clc; Mt = 1; Mr = 1; rho_dB = [0:25]; rho = 10.^(rho_dB/10); for k = 1:length(rho) for i = 1:100 H = wgn(Mr,Mt,0,’dBW’,’complex’); [F, L, M] = svd(H); for j = 1:min(Mt,Mr)

sigma(j) = L(j,j); end sigma_used = sigma(1:rank(H)); gamma = rho(k)*sigma_used; %% Now we do water filling\ gammatemp = gamma; gammatemp1 = gammatemp; gamma0 = 1e3; while gamma0 > gammatemp1(length(gammatemp1)); gammatemp1 = gammatemp; gamma0 = length(gammatemp1)/(1+sum(1./gammatemp1)); gammatemp = gammatemp(1:length(gammatemp)-1); end C(i) = sum(log2(gammatemp1./gamma0)); end Cergodic(k) = mean(C); end Figure 1: Problem 10 11. We ﬁnd the capacity by randomly generating 104 channel instantiations and then averaging over it. We assume that distribution is uniform over the instantiations. MATLAB CODE clear; clc; Mt = 1; 05101520250510152025ρ (dB)CergodicMt = Mr = 3Mt = 2 Mr =3Mt = Mr = 2Mt = 2 Mr =1Mt = Mr = 1

资料库

无线通信答案goldsmith.pdf

相关推荐

课程资源

热门标签

最新资料