中国科技论文在线 http://www.paper.edu.cn 直线二级倒立摆的极点配置控制器的设计 何国瑞* （哈尔滨理工大学自动化学院，哈尔滨 150080） 摘要：对于直线二级倒立摆系统，根据其状态空间方程，我们可以设计极点配置控制器，使 得直线二级倒立摆的系统矩阵的特征值，即系统的极点转移到 S 平面的左半平面，从而使得 系统稳定。对于控制器的设计，我们基于 Ackermann 算法，求出了状态反馈矩阵 K。通过 MATLAB 仿真，可以得出设计的控制器使得系统稳定的结论。 关键词：状态控制方程；系统矩阵；Ackermann 算法；状态反馈；MATLAB 仿真 中图分类号：TP13 Linear double inverted pendulum poles placement controller design He Guorui (Automation School,harbin University of Science and Technilogy, Harbin 150080) Abstract: For linear double inverted pendulum system, according to its state-space equation, we can design poles controller, transfer the system matrix poles of linear double inverted pendulum to the left part of S planar, so that the system is stable. For the controller’s design, we base on the Ackermann’s algorithm to work out the system feedback matrix K. though the simulation of MATLAB, we may conclude that the controller design make the system stable. Key words: State Control Equation;System Matrix;Ackermann Algorithm;State Feedback;MATLAB Simulation 5 10 15 20 25 30 0 引言 倒立摆系统是一个典型的快速、多变量、非线性和绝对不稳定的系统，对倒立摆系统的 研究在理论和方法上都有深远的意义，对倒立摆的研究归结为对非线性多变量绝对不稳定系 统的研究，其控制方法和思路对处理一般工业过程都有广泛的用途。近年来，国内外专家对 倒立摆系统进行了大量的研究，试图寻找不同的控制方法实现对倒立摆的控制，以便检查或 验证该方法对非线性和绝对不稳定系统的控制能力。在本文中，我们采用比较常规的控制方 法，即利用现代控制理论的知识，利用 Ackermann 算法，对倒立摆系统进行反馈极点配置。 并对二级倒立摆系统进行了 MATLAB 仿真研究。 1 直线倒立摆极点配置的原理 如果给出了对象的状态方程的模型，我们则希望引入某种控制器，使得闭环系统的极点 可以移动到指定的位置，因为这样可以适当地指定系统闭环极点的位置，使得其动态性能得 到很好的改进[1]。在控制理论中将这种移动极点的方法称为极点配置。 35 假定系统的状态方程为： ( ) tx ( ) ty ⎧ ⎨ ⎩ = = ( ) tAx ( ) tCx + + ( ) tBu ( ) tDu (1) 可以引入系统的状态反馈，假定进入系统的受控信号为： ( ) tu = ( ) tr − ( )tKx (2) 作者简介：何国瑞(1985-),男，研究生，倒立摆的稳定控制. E-mail: 125425697@qq.com - 1 - 

40 45 50 55 60 中国科技论文在线 其中 ( )tr 为系统的外部参考输入信号，这样可以将系统的闭环状态方程写成： http://www.paper.edu.cn ( ) ( tx A = ( ( ) C ty = iui , = 假设闭环系统期望的极点位置为 ⎧ ⎨ ⎩ 成： ( ) s α = n ∏ i = 1 ( us − i ) = n s + s α 1 n − 1 + + αα + s n − 1 ( ) tBr ( ) tDr (3) ) ( ) txBK + − ) ( ) txDK + − ，则闭环系统的特征方程 ( )sα 可以表示 2,1 n (4) 对于开环状态方程模型（A,B,C,D）来说，在状态反馈向量 K 下，闭环系统的状态方程可以 写成（A-BK,B,C-DK,D）[2]。 2 直线二级倒立摆极点配置 Ackermann 算法 在这种算法中，状态反馈向量 K 可以由如下的式子得出： [ 0,0,0 −= ] ( c α1 T 1,0 − )A k 式中， ( 满秩矩阵，对单变量系统来说， (5) )Aα 为将 A 代入式（4）中得出的矩阵多项式的值[3]。如果系统完全可控，则 cT 为 cT 存在，所以可以设计出极点配置控制器[4]。MATLAB ac 函 数 来 实 现 该 算 法 ， 该 函 数 调 用 格 式 为 ： 控 制 系 统 工 具 箱 给 出 了 一 个 K (6) 其中 A 为系统状态空间方程的系统矩阵，B 为系统状态空间方程的输入矩阵，p 为期望极点 位置描述矩阵。 )pBA , ( ) ker ker ac = ( 1− , 直线二级倒立摆的状态空间方程为： x ⎡ ⎢ θ ⎢ 1 ⎢ θ 2 ⎢ x ⎢ ⎢ θ 1 ⎢ θ ⎢ ⎣ 2 y = = ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ x ⎡ ⎢ θ ⎢ 1 ⎢ θ 2 ⎢ x ⎢ ⎢ θ 1 ⎢ θ ⎢ ⎣ 2 0 ⎡ ⎢ 0 ⎢ 0 ⎢ ⎢ 0 ⎢ ⎢ 0 ⎢ 0 ⎢ ⎣ ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ = − .39 0 0 0 0 6837 3079 0 0 0 0 62.21 .86 4511 .40 − 000001 ⎤ ⎡ ⎥ ⎢ 000010 ⎥ ⎢ 000100 ⎥ ⎢ ⎥ ⎢ 001000 ⎥ ⎢ ⎥ ⎢ 010000 ⎥ ⎢ 100000 ⎥ ⎢ ⎦ ⎣ 001 010 100 000 000 000 x 0 ⎤ ⎤ ⎡ ⎥ ⎢ ⎥ 0 θ ⎥ ⎥ ⎢ 1 0 ⎥ ⎢ ⎥ θ 2 ⎥ ⎥ ⎢ x 0 ⎥ ⎢ ⎥ ⎥ ⎥ ⎢ 0 θ 1 ⎥ ⎢ ⎥ 0 θ ⎥ ⎥ ⎢ ⎦ ⎦ ⎣ 2 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ + u (7) + 0 0 0 1 6396 .6 874 .0 − ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ u 1 θθ、、x 2 其中 分别表示直线二级倒立摆系统小车的位移、摆杆 1 的角度和摆杆 2 的 角度。要使系统稳定，则系统特征方程的极点应该在是 S 平面的左半部分[5]。假定我们期望 [ −= ，则我们通过 MATlAB 软件计算 系统的极点为 出系统反馈矩阵为: 1 +− 1 −− ]i P − − − 7 6 5 8 i ] ker( K ac A B P , , [ 1.31 63.79 = = ) − 71.22 2.155 3.74 − 11.02 - 2 - 

中国科技论文在线 3 直线二级倒立摆的稳定控制仿真 http://www.paper.edu.cn x' = Ax+Bu y = Cx+Du State-Space -K- Gain -K- Gain1 -K- Gain2 -K- Gain3 -K- Gain4 -K- Gain5 Scope 1 Out1 Scope1 Scope2 Scope3 图 1 直线二级倒立摆的控制图 Figure 1. Linear double inverted pendulum control diagram 65 70 图 1 中的 state-space 模块表示的是在第二章中提出的二级倒立摆状态空间方程。它引出 的六条线即为输出，从上到下依次表示为倒立摆系统小车的位移 x 、下摆的角度 1θ 、上摆 的角度 2θ 、小车的数度 x 、下摆的角速度 1θ 、上摆的角速度 2θ 。系统的输入控制量为： ，其中 K 为状态反馈增益矩阵，已在第二章求出， X 为系统的状态变量组，即 KX u −= [ x X θθ = 1 2 这样得到： x u 31.1 在图中表示为每个状态变量依次乘以相应的比例系数然后相加得到算式和就为系统的 (8) θθ 1 2 + 02.11 22.71 θ 2 79.63 θ 1 155.2 x θ 2 − 74.3 θ 1 x − −= 。 ]T + − 控制量u 。 75 在 state-space 模块中可以设置系统状态变量组 X 的初始值，在这里我们设定初始值为： ( tX ) 0 = [ ]T 1.01.01.01.01.01.0 (9) 最后运行系统的控制仿真图，我们从依次从上而下的示波器中依得到下面的仿真图： 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 e d u t i l p m A 80 -0.8 0 1 2 3 4 5 Time(sec) 6 7 8 9 10 图 2 直线二级倒立摆的仿真图 Figure 2 Linear double inverted pendulum simulation diagram - 3 - 

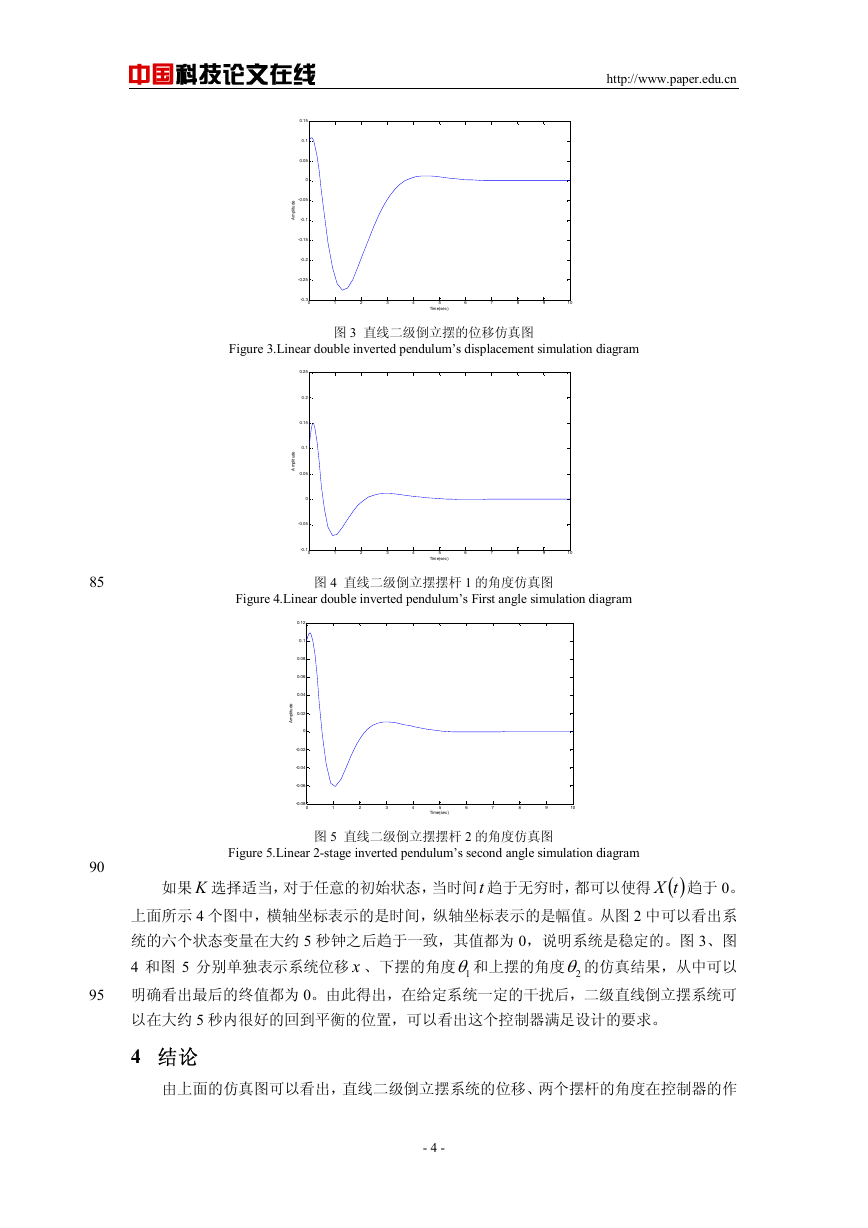
中国科技论文在线 http://www.paper.edu.cn Figure 3.Linear double inverted pendulum’s displacement simulation diagram 图 3 直线二级倒立摆的位移仿真图 图 4 直线二级倒立摆摆杆 1 的角度仿真图 Figure 4.Linear double inverted pendulum’s First angle simulation diagram 0.15 0.1 0.05 0 e d u t i l p m A -0.05 -0.1 -0.15 -0.2 -0.25 -0.3 0 1 2 3 4 5 Time(sec) 6 7 8 9 10 e d u t i l p m A 0.25 0.2 0.15 0.1 0.05 0 -0.05 -0.1 0 1 2 3 4 5 Time(sec) 6 7 8 9 10 e d u t i l p m A 0.12 0.1 0.08 0.06 0.04 0.02 0 -0.02 -0.04 -0.06 -0.08 0 1 2 3 4 5 Time(sec) 6 7 8 9 10 85 90 95 图 5 直线二级倒立摆摆杆 2 的角度仿真图 Figure 5.Linear 2-stage inverted pendulum’s second angle simulation diagram 如果 K 选择适当，对于任意的初始状态，当时间t 趋于无穷时，都可以使得 ( )tX 趋于 0。 上面所示 4 个图中，横轴坐标表示的是时间，纵轴坐标表示的是幅值。从图 2 中可以看出系 统的六个状态变量在大约 5 秒钟之后趋于一致，其值都为 0，说明系统是稳定的。图 3、图 4 和图 5 分别单独表示系统位移 x 、下摆的角度 1θ和上摆的角度 2θ 的仿真结果，从中可以 明确看出最后的终值都为 0。由此得出，在给定系统一定的干扰后，二级直线倒立摆系统可 以在大约 5 秒内很好的回到平衡的位置，可以看出这个控制器满足设计的要求。 4 结论 由上面的仿真图可以看出，直线二级倒立摆系统的位移、两个摆杆的角度在控制器的作 - 4 - 

中国科技论文在线 http://www.paper.edu.cn 用下都达到了稳定。由此可以得出对于一个可控的系统，不管系统是单输入单输出的还是多 输入多输出的，基于极点配置的状态反馈控制器，都能够控制系统的每个变量，将系统的极 点配置到预期的位置，从而达到期望的控制效果[6]。在掌握了控制算法后,即可以利用计算机 计算反馈矩阵 K 的值[7]，这样系统控制器不仅结构简单，而且操作方便，很容易应用于工程 实践中，通过仿真分析进一步证明了这种控制方法是十分有效的。 致谢 首先感谢我的导师武俊峰教授，对哈尔滨理工大学自动化学院表示感谢，还有对研究生 肖乐、李金万表示感谢！ [参考文献] (References) [1] 段广仁.线性系统理论[M].哈尔滨：哈尔滨工业大学出版社，2006 [2] 吴晓燕、张双远.MATLAB 在自动控制中的应用[M].西安：西安电子科技大学出版社，2005. [3] 郑大钟.线性系统理论[M].北京：清华大学出版社，2005. [4] 李友善.自动控制原理[M].北京：国防工业出版社，2007. [5] 郑大钟.现代控制理论[M].北京：清华大学出版社,1978. [6] 胡寿松.自动控制原理[M].北京：科学出版社，2002. [7] 郑大钟.矩阵特征多项式的一种简易算法[J].清华大学学报，1985,25(2):60-68. 100 105 110 115 - 5 -