LSTM公式详细推导.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：0.13M 资料格式：pdf 举报版权申诉

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第1页.png

第1页 / 共7页

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第2页.png

第2页 / 共7页

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第3页.png

第3页 / 共7页

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第4页.png

第4页 / 共7页

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第5页.png

第5页 / 共7页

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第6页.png

第6页 / 共7页

b77acaf9-4c53-4242-8b5a-cb7c892f9fa5.pdf-第7页.png

第7页 / 共7页

文本预览

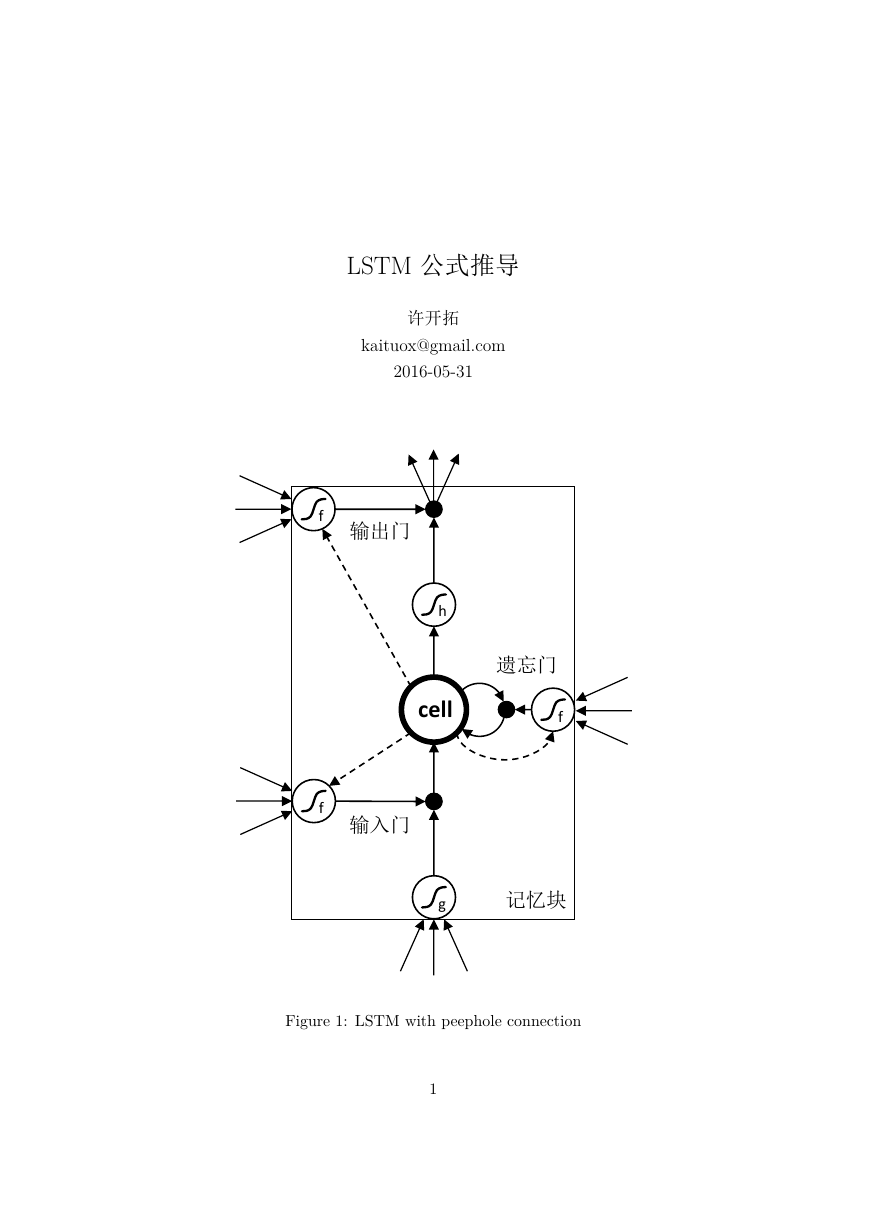
LSTM 公式推导许开拓 kaituox@gmail.com 2016-05-31 Figure 1: LSTM with peephole connection 1 fhfgfcell

1 FORWARD PASS 2 本节介绍隐层为 LSTM 的 RNN 的前向传播过程。与之前相同，定义 wij 为从单元 i 到单元 j 的连接的权值，单元 j 在 t 时刻的输入用 at j 表示， j 表示。下面只给出了包含一个记忆块的 LSTM 的前向该单元的激励用 bt 传播公式，对于包含多个块的 LSTM，只需以任意顺序对每个块重复下述计算即可。下标 ι，ϕ 和 ω 分别对应该记忆块的输入门、遗忘门和输出门。下标 c 对应一个记忆块中 C 个记忆单元中的一个，C 一般取 1，此处取 1。从单元 c 到输入门、遗忘门和输出门的 peephole 权值分别用 wcι、wcϕ 和 wcω 表示。st c 是单元 c 在 t 时刻的状态。f 是每个门的激励函数，g 和 h 分别是记忆单元的输入和输出的激励函数。 I 表示输入单元的个数，K 表示输出单元的个数，H 表示隐层的记忆 c 和隐层中的其他记忆块相连的，LSTM 的单元数。只有记忆单元的输出 bt 单元状态、单元的输入或门的激励值都只在块中可见。我们用下标 h 来标识隐层中其他块的输出，和标准的隐单元完全一样，此处的 bt h 相同。不同于标准的 RNN，一个 LSTM 层的输入比输出多，因此定义 G 为隐层总的输入数，包括记忆单元和各个门的输入，当我们不区分输入类型时，使用 g 表示这些输入。对于每个记忆块包含一个记忆单元的标准 LSTM 而言，G = 4H。 c 与 bt 和标准的 RNN 一样，前向传播是在一个长度为 T 的输入序列 x 上从 t = 1 时刻开始递归地计算所有的激励值，直到 t = T 时刻，t = 0 时刻所有的状态和激励都初始化为零。在前向传播和反向传播过程中，下述公式的计算顺序非常重要，应该严格按照下述顺序进行计算。 1 Forward Pass 1.1 Hidden Layer Input Gates I∑ at ι = wiιxt i + i=1 ι = f (at bt ι) H∑ h=1 C∑ c=1 wcιst−1 c whιbt−1 h + (1) (2)

2 BACKWARD PASS Forget Gates at ϕ = I∑ wiϕxt i + H∑ h=1 whϕbt−1 h + C∑ c=1 wcϕst−1 c Cells i=1 bt ϕ = f (at ϕ) at c = I∑ H∑ whcbt−1 h wicxt i + C∑ c=1 wcωst c h=1 ιg(at c) i=1 ϕst−1 c + bt H∑ st c = bt I∑ wiωxt i + whωbt−1 h + Output Gates at ω = i=1 bt ω = f (at ω) Cell Outputs h=1 1.2 Output-Layer bt c = bt wh(st c) C∑ c=1 at k = wckbt c 2 Backward Pass 2.1 Multi-class tasks. Network Outputs k = P (Ckjx) = yt k∑ eat k′ k′=1 eat K Loss function Lt = K∑ L = T∑ k=1 ( k ln yt zt k K∑ k ln yt zt k) t=1 k=1 3 (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)

2 BACKWARD PASS Gradient descent def = δt j ∂L ∂at j = w(m) ∂L ∂wij ij = w(m+1) ij ∆wij = T∑ α∆wij ∂L ∂at j t=1 T∑ t=1 δt j ∂at j ∂wij ∂at j ∂wij = 2.2 Output Layer ∑ ∂at k k′ ln yt k′) T t′=1( K k′=1 zt ′ ′ k′ ln yt k′) ∂ = t=1 δt kbt c ( ∑ ∑ T∑ ∂L ∂(∑ ∂at k ∑ ∑ k∑ eat k′′ k′′=1 eat zt K k′=1 zt ∂at k k′ ln K k′=1 zt ∂at k k′′ ) k′′=1 eat ∂at k zt ∂(ln ∂ K K k = yt k k ∆wck = δt k = = = = = ) ∑ ∑ K k′′ k′′=1 eat ∂ ∑ K k′=1 zt k′ ∂ k′ ln eat k′ K k′=1 zt ∂at k K k′=1 zt ∂at k k′at k′ 4 (13) (14) (15) (16) 2.3 Hidden Layer 此时要更新的参数如下：wiw、whw、wcw、wic、whc、wiϕ、whϕ、wcϕ、 wiι、whι、wcι.

2 BACKWARD PASS 2.3.1 Part 1 5 T∑ t=1 δt wxt i ∂at w ∂wiw = T∑ h = ∂L ∂at w t=1 t=1 ∆wiw = ∆whw = wbt−1 δt ∂L T∑ ∂wiw T∑ ∆wcw = ∂L ∂bt c c 与 bt h 是一回事。at ι 、at+1 c 、at+1 δt wst c def = ϵt c t=1 此处可以认为 bt 有关，且 L 与 at+1 g 索引，G=4H。由多元函数链式求导法得 ϕ 、at+1 k、at+1 ι 、at+1 ω 均与 bt c ω 有关，且将这四部分合在一起，用 ϕ 、at+1 c 、at+1 Cell Outputs ϵt c = K∑ K∑ k=1 = k=1 Output Gates ∂L ∂at k ∂at k ∂bt c ∂L ∂at+1 g ∂at+1 g ∂bt c δt kwck + δt+1 g wcg + g=1 G∑ G∑ C∑ g=1 δt w = ∂L ∂at w = ∂bt c ∂bt w ∂L C∑ ∂bt c ∂bt w ∂at w c=1 ′ 2.3.2 Part 2 = f (at w) ch(st ϵt c) c=1 T∑ t=1 = ∂L ∂at c ∂at c ∂wic = T∑ t=1 cxt δt i ∆wic = ∂L T∑ ∂wic ∆whc = ∂L ∂st c def = ϵt s t=1 cbt−1 δt h (17) (18)

6 (19) (20) 2 BACKWARD PASS ϕ 、sct + 1、at ω、bt c 均与 st c 有关 ι 、at+1 at+1 States ∂Lt+1 ∂at+1 ι ∂at+1 ι ∂st c + c + ∂Lt+1 ∂st+1 ∂Lt ∂bt c ∂bt ∂st c c ∂Lt+1 ∂at+1 ϕ ∂at+1 ∂st c ϕ ′ c + bt+1 c)ϵt wh (st + ∂st+1 c ∂st c ∂at ω ∂st c ∂Lt ∂at ω s + wcιδt+1 ϕ ϵt+1 ϵt s = + = bt ι + wcϕδt+1 ϕ + wcωδt ω Cells 2.3.3 Part 3 δt c = ∂L ∂at c ∂L ∂st c ∂st c ∂at c = = ϵt cbt ιg ′ (at c) T∑ t=1 = δt ϕxt i ∂L T∑ ∂wiϕ T∑ t=1 ϕbt−1 δt h ϕst−1 δt c ∆wiϕ = ∆whϕ = ∆wcϕ = t=1 Forget Gates δt ϕ = ∂L ∂at ϕ = C∑ c=1 ∂L ∂st c ∂st c ∂bt ϕ ∂bt ϕ ∂at ϕ ′ (at ϕ) = f C∑ c=1 st−1 c ϵt s (21) 2.3.4 Part 4 T∑ t=1 = δt ιxt i ∂L T∑ ∂wiι T∑ t=1 ιbt−1 δt h ιst−1 δt c ∆wiι = ∆whι = ∆wcι = t=1

2 BACKWARD PASS 7 Input Gates δt ι = ∂L ∂at ι = C∑ c=1 ∂L ∂st c ∂st c ∂bt ι ∂bt ι ∂at ι ′ (at ι) = f C∑ c=1 g(at c)ϵt s (22)

分享到：

赞收藏

资料库

LSTM公式详细推导.pdf

相关推荐

课程资源

热门标签

最新资料