第1页 / 共23页
第2页 / 共23页
第3页 / 共23页
第4页 / 共23页
第5页 / 共23页
第6页 / 共23页
第7页 / 共23页
第8页 / 共23页
2019年美国大学生数学建模竞赛（MCM）B题特等奖论文 .pdf
Introduction
Assumptions and Justification
Transportation Capability Evaluation Model
Assumptions in This Model
Three Space Division Model
Putting MEDs into Bays
Drone Transport Capability Model
Putting Drones and Bays into Cargo Conatainers
Monte-Carlo Simulation And Results
Geospatial Analysis Model
Drone Reconnaissance Model
Geographical Features
Singal Location Determination
Multiple Locations Determination
Results
Fleet Arrange Model
Schedule Arrangement Model
Drone Route Planning Model
Sensitivity Analysis
Strengths and Weaknesses
Strengths
Weaknesses
Conclusion
For office use only
T1
T2
T3
T4
Team Control Number
1908286
Problem Chosen
B
For office use only
F1
F2
F3
F4
2019 MCM/ICM Summary Sheet
Hurricane Maria Damage left Puerto Rico people a lot of pain and devastation. HELP,Inc., an NGO,
is attempting to improve its response capabilities by designing a transportable disaster response system
called "DroneGo".
In order to better assess the transport capability of the drone fleet, we establish a Transport Capability
Evaluation Model of the drone fleet, so that we can maximize the medicine transportation capability of
the drone fleet when the disaster location is unknown. In this model, we use the algorithm of linear
programming to solve the limitations of volume, weight and other simple factors. After that, we used
an algorithm based on three-space segmentation and improved Monte Carlo simulation to solve the size
limitation of the objects. As a result, we obtain a reliable evaluation of the transport capability of drones,
and it can be found that among the drones, the transportation capability of drone G is the strongest.
Through the research on the reconnaissance method of the drones, we get the Reconnaissance Ca-
pability Model of the drone fleet. In this model, we find that the reconnaissance capability of drone
B is the strongest. Based on these two models (TCM & RCM) and abundant geographic information,
we developed a Geospatial Analysis Model. We employ the Analytical Hierarchy Process (AHP) in the
space of all position, obtaining a spatial distribution of drone fleet ˛a´rs transportation capability and re-
connaissance capability. Then, we establish an overall Efficiency Evaluation Model for the drone fleet,
using a nonlinear programming with a variable parameter to obtain the optimal solution of the drone
fleet overall efficiency and its spatial location. Consequently, we can determine a configuration of the
drone fleet and each container’s drop point. DroneGo users can also adjust the variable parameter de-
pending on whether they care more about their fleet ˛a´rs transport capability or reconnaissance capability
to determine different options. For the problem of multiple containers, we use a dynamic programming
rule that allows users to arrange multiple containers.
In considering that the transportation capability of the drone fleet is as important as the reconnais-
sance capability, we get results that the medicine delivery can be maintained for more than two months
and road reconnaissance coverage can reach nearly 60%. Meanwhile we construct an efficient Schedule
Arrangement Model and Route Arrangement Model of drones using an integer programming model
and an improved greedy algorithm, so that the drone fleet can be auto arranged.
The sensitivity analysis shows the strong robustness of our model. Meanwhile, we further discuss
the possibility of developing a DroneGo system software, and provide practicable advice to the HELP,
Inc. CEO.
Keywords: Multi-Objective Programming,Dynamic Programming, Drone Rescue Model, AHP
Team # 1908286
Page 1 of 22
Contents
1
Introduction
2 Assumptions and Justification
3 Transportation Capability Evaluation Model
3.1 Assumptions in This Model
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Three Space Division Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Putting MEDs into Bays .
3.4 Drone Transport Capability Model
. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5 Putting Drones and Bays into Cargo Conatainers . . . . . . . . . . . . . . . . . . .
3.6 Monte-Carlo Simulation And Results . . . . . . . . . . . . . . . . . . . . . . . . . .
.
4 Geospatial Analysis Model
4.1 Drone Reconnaissance Model
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Geographical Features .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Singal Location Determination . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4 Multiple Locations Determination . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5 Results .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
5 Fleet Arrange Model
5.1 Schedule Arrangement Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Drone Route Planning Model
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6 Sensitivity Analysis
7 Strengths and Weaknesses
.
.
7.1 Strengths .
7.2 Weaknesses
.
.
.
.
.
.
.
.
.
8 Conclusion
.
.
.
.
.
.
. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2
3
3
3
5
6
7
7
8
8
9
10
13
14
14
14
16
19
19
19
20
20
Team # 1908286
Page 2 of 22
An optional Design of DroneGo
1
Introduction
People in disaster areas are in great need of timely emergency services. [1] Drones can help
a lot in emergency rescue. According to a drone manufacturer DJI [2], drones have saved 59
lives since 2013.
In this paper, we will
• Analyze three dimensional packing problem and develop Three Space Division Model
and improved Monte-Carlo Simulation to solve the problem of packing restrictions in the
transportation.
• Analyze the transportation capability and detective capability of each Drone type,apply
AHP method to considers the influence of many possible factors on the selection of con-
tainer drop location , including transportation, population, geography and medical infor-
mation.
• Build a model to determine drone payload packing configuration and solve it with a com-
• Improve greedy algorithm and figure out the drone route planing quickly and accurately.
plex integer programming quickly and accurately.
2 Assumptions and Justification
We make some general assumptions to simplify our model. These assumptions together
with corresponding justification are listed below:
• There are no charging devices for drones. In 2017, Hurricane Maria knocked down 80%
of Puerto Rico’s utility poles and all transmission lines. We can infer that electricity are
not available on the island. Our Cargo will not include charging equipment or generating
set, due to extra weight and inconvenience.
• The cargo weight does not influence the maximum flight distance of a drone. That
is, maximum flight distance is exactly the same with or without a cargo. We make the
assumption for simplicity. In reality, the weight of a delivery drone is often larger than
that of its cargo. It is quite reasonable to neglect the influence of cargo weight. And this
will greatly simply our model.
• For each Cargo Container, we will load one tethered Drone (type H). In natural disasters,
communication facilities are often affected to various degrees, and emergency communi-
cation becomes an urgent need. It can act as an emergency communication base station.
Tethered drones will greatly enhance the disaster response capability of DroneGo system.
• One drone can carry one drone cargo bay or no bay for every flight. If the drone carries
one, it can only deliver the bay to one location. Both of the two types of drone cargo
bay are "top loaded", that is, loaded on the top of a drone. If we distribute more than one
bay at a flight, connections between cargo bays could be unstable. We can deliver a drone
cargo bay to only one place since it is an integral package that cannot be open in transit.
• Helicopters can transport cargo containers to any given place in the disaster area. In
disaster-affected areas, timely external assistance is urgently needed to restore order. There-
fore, we consider air transportation rather than sea transportation. Although Puerto Rico
is an island, air transportation will bring adaptability to our model in other situations.
• Communication and data transmission of drones are always available. We can achieve
telecommunication by radio communication or satellite communication. Drone commu-
nication dose not rely on ground devices.
Team # 1908286
Page 3 of 22
• For the ith type of drone, its maximum Flight Distance, denoted by Disti is in direct
proportion to the product of Speed and F lightT ime(N o Cargo). From that assumption,
we have Disti = α × Speed × F light T ime (N o Cargo), where α represents distance-loss
coefficient. Here we neglect the effect of weather (especially wind) and different battery
and motor of different drones of a specific type. To determine α, we note that there are
mostly mountains with few plains. And Puerto Rico has a mean elevation of 261 m. [3] The
high elevation shortens the maximum flight distance. We have α < 1. For simplification,
we choose α = 0.9.
More detailed assumptions will be listed if needed.
3 Transportation Capability Evaluation Model
In this section, we will evaluate transportation ability of each type of drones. For simplicity,
we will focus on the need of medical transportation here. We will incorporate road reconnais-
sance into our model in Section 5.
3.1 Assumptions in This Model
We will use the following assumptions in this section:
• All Cargo Containers(CC), Drone (in shipping containers), Drone Cargo Bays (DCB),
• Drones and Drone Cargo Bays should be placed into Cargo Containers in parallel,
which is "parallel placement". That is, the inner subface of Drones or Bays must be par-
allel to the corresponding surface of the Cargo Container. There are two reasons. For one
thing, the parallel placement is one of the most commonly used packing methods. For
another thing, cargos can be easily placed in this way and have a high stability.
• The thickness of Drone Cargo Bays can be neglected.
• Goods can be arbitrarily rotated, but must still satisfy the "parallel placement" condi-
• As is interpreted in the problem description, each Cargo Container’s contents should
be packed, so all Medical Packages should be packed in Drone Cargo Bays. We do not
consider Medical Packages directly placed in a Cargo Container.
and Medical packages (MP) are cuboids.
tion.
3.2 Three Space Division Model
3.2.1 One Goods Condition
To design a packing configuration for DroneGo, we need to put MEDs into Bays and put
Bays or Drones into Containers. Due to various kinds of goods in the problem, this is a three-
dimensional heterogeneous container loading problem. We use the Three Space Division
Method and Monte Carlo Simulation to solve it.
Note that we refer to a rectangular container that contains goods as a box. As is shown in
Figure 1, L, W and H is the length, width and height of the container, respectively. Similarly,
l, w and h is the length, width and height of the cargo, respectively. We set up a Cartesian
coordinate at the left bottom vertex of the container. Note that we consider the position of the
container is unchanged. We put the cargo into the container, so that two left bottom vertexes
coincide. Arrangement problem is a way to think about ways to put the cargo. To put
Team # 1908286
Page 4 of 22
h into x, y and z coordinates, we have A3
is, there are six possible combinations of the coordinates of the diagonal vertex of the cargo.
3 = 6. There are six ways to put the cargo inside. That
Figure 1: Three Space Division
For every specific combination, we can see that the rest space in the container are cut into
three parts (spaceX, spaceY and spaceZ) , see figure 1. One possible sequence (shown in Figure
1) to generate the three parts is
1. Procedure X: Cut the remaining space using a plane perpendicular to the X-axis and get
2. Procedure Y: Cut the remaining space using a plane perpendicular to the Y-axis and get
3. Procedure Z: Cut the remaining space using a plane perpendicular to the Z-axis and get
spaceX.
spaceY.
spaceZ.
We refer to this sequence as a X-Y-Z sequence. The rest are similar. Arrangement problem
is a way to think about the space cutting process. To generate a sequence from procedure X, Y
and Z we have A3
3 = 6.
Thus, if a cargo can be put into the cargo, we have the total cases of three space division:
6 × 6 = 36 Then we consider every new space as a new container. And the three space division
process goes on, until the cargo can not be put into any of the existing containers. In this way,
we can traverse all situations and find the optimal solution for a specific objective function.
3.2.2 Multiple Goods Condition
To clarify the problem, we will use the following notations:
• K = {1, 2, . . . ,|K|} is the set of Boxes’ number;
• R = {1, 2, . . . ,|R|} is the set of goods’ types;
• Mr = {1, 2, . . . ,|Mr|} is the set of goods’ number (same type) ;
• sB = (L W H)T is Box Size column vector;
• sG
• Xk is the number of goods in the kth box;
•
r = (lr wr hr)T is the rth type of Goods Size column vector;
if the mth Goods of Type r is in Box k
Ykrm =
0, otherwise
1,
1,
is an Existing Flag;
• u = (xkrm ykrm zkrm)T is coordinates of the mth goods of Type r in Box k;
•
if the length of the mth Goods of Type r is parallel to the x-axis
lxrm =
0, otherwise
is a Configuration Variable;
lxrm
•
P =
lyrm
lzrm
wxrm wyrm wzrm
hxrm hyrm hzrm
is Configuration Matrix.
Team # 1908286
Page 5 of 22
Undefined elements in the matrix is defined similarly to lxrm.
In multiple-goods-condition, we consider the container loading problem as a Single-objective
integer programming problem. Constraint Conditions of the three-dimensional heterogeneous
container loading problem are listed below:
1. Boxes should contain all goods:
2. Corresponding Rule. Each goods should be placed into just only one box:
|K|
k=1
Xk =
Mr
|R|
|K|
r=1
k=1
3
∀r ∈ R,∀m ∈ Mr,
Ykmr = 1
3
pab = 1
pab = 1.
3. Configuration Constraint. Each edge in each goods should be parallel to just only one
edge of the corresponding box. Let P = (pab)3×3, we have
a=1
b=1
4. Box Size Constraint. All goods should be inside the corresponding box:
∀k ∈ K,∀r ∈ R,∀m ∈ Mr, Ykrm(u + P · sG
r ) ≤ sB
We can solve the programming problem with a specific objective function.
3.3 Putting MEDs into Bays
Since there are only three types of MEDs and two types of Bays, putting MEDs into Bays
is relatively simple. In 3D heterogeneous container loading problems, space utilization(SU)
usually decreases as type of goods R increases. For simplicity, we only consider two types of
MEDs or less in a Bay. We do not need to consider an objective function in this process. Rather,
we list all possible combinations subject to its constraint conditions.
Let R = {1, 2, 3}, whose elements 1, 2 and 3 correspond to MED1, MED2 and MED3, re-
spectively. And |Mr| is the number of MEDr. For type q Bay (q = 1, 2), we have the following
constraint conditions:
where sB
1 = (8 10 14)T, sB
Capability(M P Ci):
|K|
k=1 Xk =3
|K|
3
k=1 Ykmr = 1,∀r ∈ R,∀m ∈ Mr
3
a=1 pab = 1
b=1 pab = 1
r=1 Mr
Ykrm(u + P · sG
2 = (24 20 20)T.
r ) ≤ sB
q ,∀k ∈ K,∀r ∈ R,∀m ∈ Mr
,
(1)
For type i Drone, an additional constraint is that total weight cannot exceed Max Payload
2|M1| + 2|M2| + 3|M3| ≤ M P Ci
(2)
(1 and (2) determine whether we can put a set of MEDs into a Bay. If that set of MEDs works,
we calculate its space utilization:
3
r=1 (|Mr|lrwrhr)
,
LqWqHq
SU =
Team # 1908286
Page 6 of 22
where (l1 w1 h1)T = (14 7 5)T, (l2 w2 h2)T = (5 8 5)T, (l3 w3 h3)T = (12 7 4)T, (L1 W1 H1)T =
(8 10 14)T, (L2 W2 H2)T = (24 20 20)T.
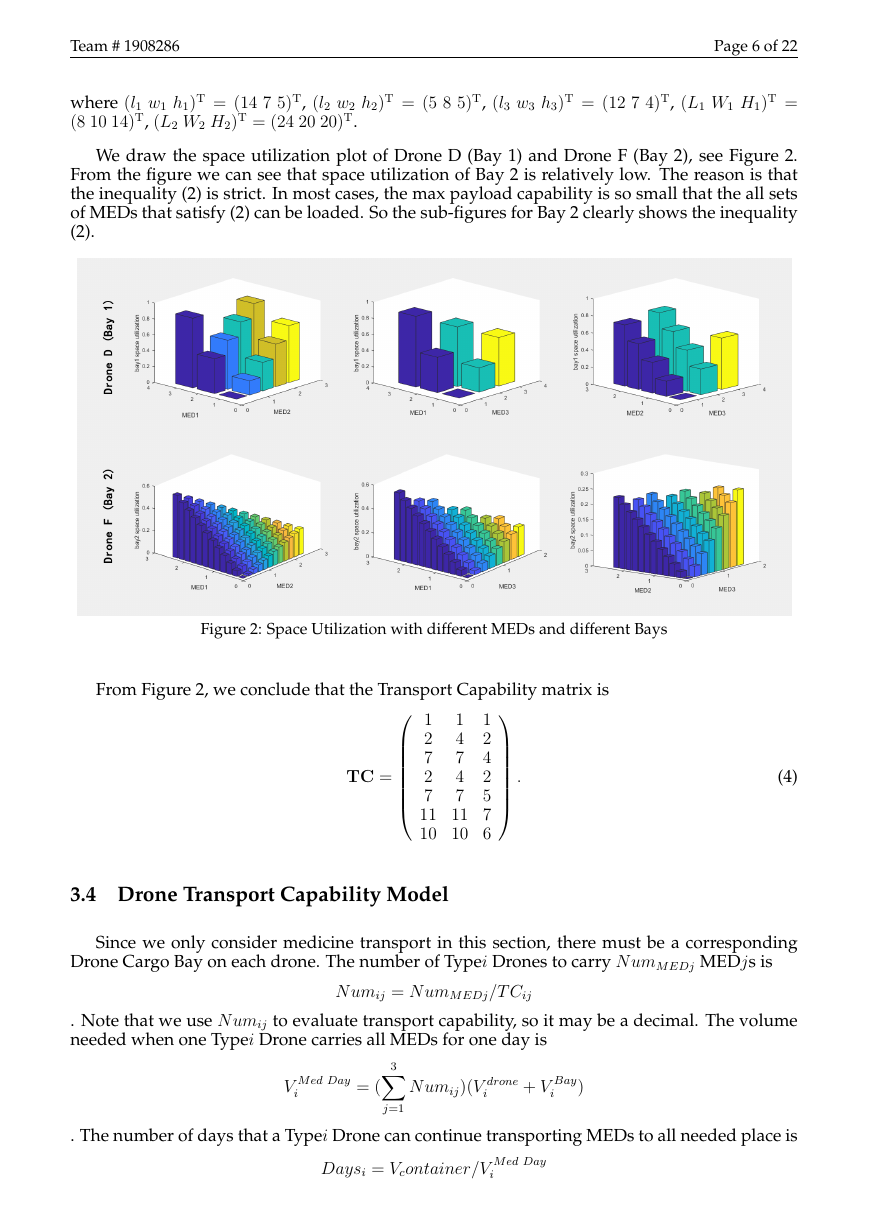
We draw the space utilization plot of Drone D (Bay 1) and Drone F (Bay 2), see Figure 2.
From the figure we can see that space utilization of Bay 2 is relatively low. The reason is that
the inequality (2) is strict. In most cases, the max payload capability is so small that the all sets
of MEDs that satisfy (2) can be loaded. So the sub-figures for Bay 2 clearly shows the inequality
(2).
Figure 2: Space Utilization with different MEDs and different Bays
From Figure 2, we conclude that the Transport Capability matrix is
1
4
7
4
7
1
1
2
2
4
7
2
2
7
5
11 11 7
10 10 6
.
TC =
(4)
3.4 Drone Transport Capability Model
Since we only consider medicine transport in this section, there must be a corresponding
Drone Cargo Bay on each drone. The number of Typei Drones to carry N umM EDj MEDjs is
N umij = N umM EDj/T Cij
. Note that we use N umij to evaluate transport capability, so it may be a decimal. The volume
needed when one Typei Drone carries all MEDs for one day is
3
V M ed Day
i
= (
N umij)(V drone
i
+ V Bay
i
)
. The number of days that a Typei Drone can continue transporting MEDs to all needed place is
j=1
Daysi = Vcontainer/V M ed Day
i
Team # 1908286
Page 7 of 22
Transport Capability Index of Typei Drone is defined as the normalization of maximum day
Daysi:
T CIi = Daysi/ max
1≤k≤7
{Daysk}
We have two matrices:
2.97
15.92
8.78
24.45
41.46
28.98
47.21
TCI =
0.0629
0.3371
0.1859
0.5178
0.8782
0.6139
1.0000
Days =
(5)
3.5 Putting Drones and Bays into Cargo Conatainers
According to TCI matrix (5), Type E and G Drones have the best transport capability. We
will choose Type E and G as alternative transport drones. The corresponding Bays are Bays 2.
We will also load one Drone H (tethered drone) in each Cargo Container, because it helps to
build emergency communication.
Let R = {4, 5, 6, 7}. 4, 5, 6 and 7 represent Bay 2, Drone E, H and G, respectively. The number
of MEDs in Bay 2 only relies on Type i drone’s Max Payload Capability M P Ci. So we conclude
that for Drone fleet consisting of E and G, transport capability is only relevant to Total Load
Weight:
T LW =
M P Ci × |Mi| = 15|M5| + 20|M7|
(6)
i=5,7
Our problem can be stated as
max T LW = 15|M5| + 20|M7|
Equation (??) shows that each Drone must carry one Bay, so the total number of Drones E
and G equal to the number of Bays 2. Equation (??) shows that each Cargo Container should
have one Type H Drone.
3.6 Monte-Carlo Simulation And Results
We use Monte-Carlo Simulation to get a satisfactory solution of the problem in Section 4.5.
Since this is a NP-completeness problem, it takes too long to traverse all situations. Our objec-
tive function will not have major changes with a narrow change of inputs. That is, the optimal
point is not an isolated singularity. That’s why we choose Monte-Carlo Simulation.
If the probability to find the optimal point is 10−5 for one simulation, the probability to find
the optimal point will be 1 − 0.999991000000 = 0.999954 with one billion simulations. Figure 3
is our simulation process using Three Space Division method. We start at a feasible solution
|M4| = 50,|M5| = 30,|M6| = 1,|M7| = 20.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
