第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
（研究生 数理统计）多元线性回归及显着性检验Matlab程序（完美版）.doc
多元线性回归及显著性检验 Matlab 程序（完美版）
一、说明：
1、本程序是研究生教材《数理统计》（杨虎、刘琼、钟波 编著） 例 4.4.1（P133）的 Matlab
编程解答程序。教材上的例题只做了回归方程显著性分析和一次回归系数显著性分析（剔
除 x1 后没有再检验 x2 和 x3）。
2、本程序在以上的基础之上，还分别检验了 x2 和 x3，并且计算精度更高。
3、本程序可根据用户的需要，在输入不同的显著性水平α之下得到相应的解答。
4、本程序移植性强，对于其他数据，只需要改变 excel 中的数据即可。
5、本程序输出的可读性强，整洁美观。
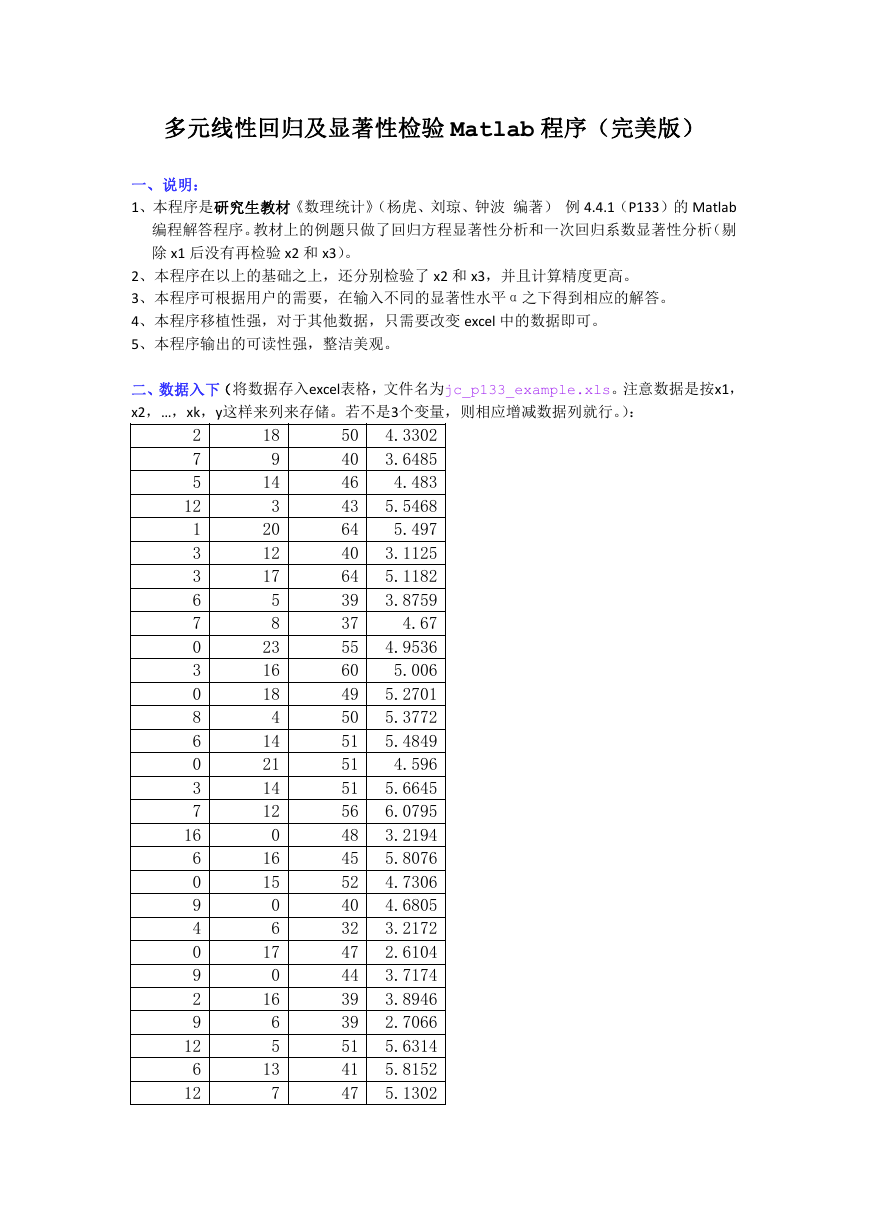
二、数据入下（将数据存入excel表格，文件名为jc_p133_example.xls。注意数据是按x1，
x2，…，xk，y这样来列来存储。若不是3个变量，则相应增减数据列就行。）：
2
7
5
12
1
3
3
6
7
0
3
0
8
6
0
3
7
16
6
0
9
4
0
9
2
9
12
6
12
18
9
14
3
20
12
17
5
8
23
16
18
4
14
21
14
12
0
16
15
0
6
17
0
16
6
5
13
7
50
40
46
43
64
40
64
39
37
55
60
49
50
51
51
51
56
48
45
52
40
32
47
44
39
39
51
41
47
4.3302
3.6485
4.483
5.5468
5.497
3.1125
5.1182
3.8759
4.67
4.9536
5.006
5.2701
5.3772
5.4849
4.596
5.6645
6.0795
3.2194
5.8076
4.7306
4.6805
3.2172
2.6104
3.7174
3.8946
2.7066
5.6314
5.8152
5.1302
0
5
4
0
6
4
10
4
5
9
6
5
5
8
2
7
4
10
3
4
24
12
15
20
16
17
4
14
13
8
13
8
11
6
13
8
10
5
17
15
61
37
49
45
42
48
48
36
36
51
54
100
44
63
55
50
45
40
64
72
5.391
4.4533
4.6569
4.5212
4.865
5.3566
4.6098
2.3815
3.8746
4.5919
5.1588
5.4373
3.996
4.397
4.0622
2.2905
4.7115
4.531
5.3637
6.0771
三、完整程序如下：
%----------------------------by ggihhimm----------------------------
%《数理统计》杨虎、刘琼、钟波 编著 例 4.4.1 多元线性回归及显著性检验 完整解答
% 输入需要的显著水平α（默认α=0.02），计算出不同结果（见运行结果）
% 该程序也适合其他维数的数据分析（只需改变 excel 表格中的数据即可）
%----------------------------by ggihhimm----------------------------
clear;clc;
data=xlsread('jc_p133_example.xls','sheet1');
xi=data(:,1:end-1);
[n,k]=size(data);
k=k-1;
index_of_xi_array=ones(1,k);
X=[ones(n,1) xi];
Y=data(:,end);
fprintf('第 1 次计算结果：\r')
beta_mao=((X'*X)\X'*Y)';
fmt_str0='';
for i0=1:k+1
fmt_str0=[fmt_str0 'β' num2str(i0-1) ' = %0.4f\r'];
end
fprintf(fmt_str0,beta_mao)
fprintf('\r')
%%检验回归方程的显著性
x_ba=mean(xi);
y_ba=mean(Y);
St_square=sum(Y.^2)-n*y_ba^2;
lxy=sum((xi-ones(n,1)*x_ba).*((Y-y_ba)*ones(1,k)));
Sr_square=sum(beta_mao(2:end).*lxy);
Se_square=St_square-Sr_square;
c_flag=Sr_square/Se_square;
F_alpha=input('>>>>>>请输入您要求的显著性水平(0<α<1)α= ');
while ~(isscalar(F_alpha) && F_alpha<1 && F_alpha>0)
F_alpha=input('您的输入有误，请重新输入一个大于 0，小于 1 的数，α= ');
end
F_fenweidian=finv(1-F_alpha,k,n-k-1);
c=k/(n-k-1)*F_fenweidian;
if c_flag>c
fprintf(['\r--------------------回归方程显著性检验（H0：β1=β2=...=βk=0）' ...
'--------------------\r 经过计算：拒绝 H0，原假设不成立。'])
fprintf(['\r--------------------回归方程显著性检验（H0：β1=β2=...=βk=0）' ...
'--------------------\r 经过计算：接受 H0，原假设成立。'])
else
end
%%检验回归系数的显著性（循环检验，直到 OK，得出最后结果）
fprintf(['\r\r-----------------回归系数显著性检验（分别对β1、β2、...、βk 进行）' ...
'------------------'])
flag_go_on=1;
num_of_loop=0;
while flag_go_on
cij=inv(X'*X);
cii=diag(cij);
F_fenweidian_1=finv(1-F_alpha,1,n-k-1);
ci=sqrt(cii(2:end)*Se_square*F_fenweidian_1/(n-k-1));
format_str='%15.4f';
for ii=1:k-1
format_str=[format_str '%13.4f'];
end
fprintf(['\r 第%d 次检验：\rcii: ' format_str '%13.4f\r ci:
' ...
format_str '\rβi：' format_str '%13.4f'],num_of_loop+1,cii,ci,beta_mao)
if ~all(abs(beta_mao(2:end))>ci')
flag_go_on=1;
beta_1tok=beta_mao;
beta_1tok(1)=[];
fi_xin=beta_1tok.^2./cii(1:end-1)';
min_fi=min(fi_xin);
beta_index=find(fi_xin==min_fi)+1;
fprintf('\rx%d 对 y 的线性影响最不显著（ |β%d|=%0.4f ）。删除 x%d，进行第%d 次计
算：',...
else
beta_index-1+num_of_loop,beta_index-1+num_of_loop,...
abs(beta_mao(beta_index)),beta_index-1+num_of_loop,...
beta_index-1+num_of_loop+1)
fmt_str2='x%d';
index_of_xi=find(index_of_xi_array);
for i2=1:length(find(index_of_xi))-1
fmt_str2=[fmt_str2 '、x%d'];
end
fprintf(['\r\r 经过检验，剩余所有变量:' ...
fmt_str2 '对 y 的线性影响均显著。检验结束。\r'],index_of_xi)
flag_go_on=0;
end
if flag_go_on
num_of_loop=num_of_loop+1;
k=k-1;
if ~k
fprintf('\r\r 警告：通过一一对所有变量做显著性检验，已剔除所有变量！');
break;
end
beta_mao=beta_mao-beta_mao(beta_index)/cii(beta_index)*cij(beta_index,:);
beta_mao(beta_index)=[];
fmt_str1='';
for i1=2:k+1
fmt_str1=[fmt_str1 'β' num2str(i1-1+num_of_loop) ' = %0.4f\r'];
end
fprintf(['\rβ0 = %0.4f\r' fmt_str1],beta_mao)
X(:,beta_index)=[];
index_of_xi_array(beta_index-1+num_of_loop-1)=0;
xi=X(:,2:end);
x_ba=mean(xi);
lxy=sum((xi-ones(n,1)*x_ba).*((Y-y_ba)*ones(1,k)));
Sr_square=sum(beta_mao(2:end).*lxy);
Se_square=St_square-Sr_square;
end
end
四、运行结果如下（分别为α=0.01 和 α=0.02 的运行结果）：
第 1 次计算结果：
β0 = 0.7344
β1 = 0.1585
β2 = 0.1063
β3 = 0.0357
>>>>>>请输入您要求的显著性水平(0<α<1)α= 0.01
-----------------------------------α = 0.0100-----------------------------------
--------------------回归方程显著性检验（H0：β1=β2=...=βk=0）--------------------
经过计算：拒绝 H0，原假设不成立。
1.1355
-----------------回归系数显著性检验（分别对β1、β2、...、βk 进行）------------------
第 1 次检验：
cii:
ci:
βi：
x1 对 y 的线性影响最不显著（ |β1|=0.1585 ）。删除 x1，进行第 2 次计算：
β0 = 2.5302
β2 = 0.0231
β3 = 0.0362
0.0055
0.1622
0.1585
0.0021
0.1006
0.1063
0.0002
0.0284
0.0357
0.7344
0.4274
第 2 次检验：
cii:
ci:
βi：
x2 对 y 的线性影响最不显著（ |β2|=0.0231 ）。删除 x2，进行第 3 次计算：
β0 = 2.6615
β3 = 0.0391
0.0006
0.0569
0.0231
0.0002
0.0302
0.0362
2.5302
第 3 次检验：
cii:
ci:
βi：
0.4079
2.6615
0.0002
0.0294
0.0391
经过检验，剩余所有变量:x3 对 y 的线性影响均显著。检验结束。
第 1 次计算结果：
β0 = 0.7344
β1 = 0.1585
β2 = 0.1063
β3 = 0.0357
>>>>>>请输入您要求的显著性水平(0<α<1)α= 0.02
-----------------------------------α = 0.0200-----------------------------------
--------------------回归方程显著性检验（H0：β1=β2=...=βk=0）--------------------
经过计算：拒绝 H0，原假设不成立。
-----------------回归系数显著性检验（分别对β1、β2、...、βk 进行）------------------
第 1 次检验：
cii:
ci:
βi：
0.0055
0.1455
0.1585
0.0021
0.0902
0.1063
1.1355
0.7344
0.0002
0.0255
0.0357
经过检验，剩余所有变量:x1、x2、x3 对 y 的线性影响均显著。检验结束。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
