2.2 离散余弦变换(DCT)
There are many other transforms that are used quite often by
engineers and mathematicians.. Hilbert transform, short-time Fourier
transform (more about this later), Wigner distributions, the Radon
Transform, and of course our featured transformation, the wavelet
transform, constitute only a small portion of a huge list of transforms that
are available at engineer's and mathematician's disposal. Every
transformation technique has its own area of application, with advantages
and disadvantages. –R. Polikar, the Wavelet Totorial
2.2.1 离散图像变换的一般表达式[4]
离散图像变换的代数表达式
对于 2-D 离散函数
yxf
,(
)
x
=
0,1,2,
,
M
−
;1
y
=
,2,1,0
L
,
N
−
1
L
有变换对
T u v
( , )
=
=
⎛
⎜
⎝
1
−
M N
1
−
∑∑
x
=
0
y
=
0
1
−
M N
1
−
∑∑
x
=
0
y
=
0
f x y g x u y v
u
) ( ,
,
( ,
)
正变换核
uuuuuuuuuuuuru
,
=
0,1,2,
L
,
M
−
v
1
=
0,1,2,
,
N
−
1
L
g x u f x y g y v
( ,
1
( , )
( ,
)
2
)
⎞
⎟
⎠
f x y
( , )
=
T u v h x u y v
( , ) ( ,
,
)
反变换核
uuuuuuuuuuuur
,
x
=
0,1,2,
,
L
M y
1
−
=
0,1,2,
,
L
N
1
−
1
−
M N
1
−
∑∑
v
0
0
=
=
M N
1
−
u
⎛
=⎜
⎝
1
−
∑∑
u
0
=
v
0
=
h x u T u v h y v
( , ) ( , )
1
( , )
2
⎞
⎟
⎠
上两式已经考虑了可分离性(Separability),变换核可分离的离
散图像变换表示为
1
�
vuT
),(
=
M
1
−
1
−
N
∑∑
0
y
x
0
=
=
N
M
1
−
1
−
)
=
∑∑
0
u
v
0
=
=
yxf
,(
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
vygyxfuxg
),(
1
),(
,(
)
2
=
=
u
v
,2,1,0
,2,1,0
,
L
,
L
vyhvuTuxh
),(
1
),(),(
M
N
2
1
−
1
−
x
y
=
=
,2,1,0
,2,1,0
,
,
M
N
1
−
1
−
L
L
如此,二维离散变换就可以用两次一维变换实现。
对傅里叶变换,正变换核
g
=
exp
−
⎡
⎢
⎣
j
⎛
π2
⎜
⎝
ux
M
+
vy
N
⎞
⎟
⎠
⎤
⎥
⎦
,实际是由正弦和
余弦函数组成;反(或说是逆)变换核
h
=
exp
⎡
⎢
⎣
j
⎛
π2
⎜
⎝
ux
M
+
vy
N
⎞
⎟
⎠
⎤
⎥
⎦
。
矩阵表达式
在二维离散傅里叶变换式(可分离变换)
vuF
),(
=
1
MN
1
M
N
1
−
∑∑−
x
=
0
y
=
0
yxf
,(
)
exp
−
⎡
⎢
⎣
j
⎛
2
π
⎜
⎝
ux
M
+
vy
N
⎞
⎟
⎠
⎤
⎥
⎦
中,令
exp
F
(0,0)
F
(1,0)
⎡
⎢
⎢
⎢
⎢
⎣
N
j
j
=
−
=
⎡
⎢
⎣
W
M
, exp
,则上式用矩阵可表示为
2
2
π⎡
Wπ
⎤
⎤
−
⎥
⎢
⎥
N
M
⎦
⎣
⎦
x=0 1 2 ..... M-1 u=
W
0
0
M
W
1
M
1)
(
−
M
W
2
1)
2(
−
M
F N
(0,
F N
(1,
F
(0,1)
F
(1,1)
W
0
M
W
2
M
W
4
M
W
0
M
W
1
M
W
2
M
1)
−
1)
−
L
L
=
M
L
L
L
⎤
⎥
⎥
⎥
⎥
⎦
1
MN
⎡
W
0
M
⎢
W
0
⎢
M
⎢
W
0
M
⎢
⎢
M
⎢
W W
(
⎢
⎣
M
0
M
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦-
M
M
1)
−
M
W
M
2(
M
1)
−
L
2
1)
−
M
W
(
M
M
M 1
W
0
N
W
1
N
W
2
N
y=0 1 2 ..... N-1 v=
⎡
W
0
N
⎢
W
0
⎢
N
⎢
W
0
N
⎢
⎢
M
M
⎢
W W
N
(
⎢
⎣
N
⎤
⎥
⎥
⎥
⎥
⎥
N 1
-
⎥
⎥
⎦
W
0
0
N
W
1
N
(
1)
−
N
W
2
2(
N
W
0
N
W
2
N
W
4
N
M
W
N
2(
N
L
L
L
W
(
N
L
M
N
0
N
1)
−
1)
−
1)
−
1)
−
N
2
×
M
−
F M
(
1,0)
F M
(
1,0)
L
M
−
M
1,
−
F M N
(
−
1)
f
f
(0,0)
(1,0)
f
f
(0,1)
(1,1)
M
−
1,0)
f M
(
M
f M
(
−
1,1)
L
L
L
f
N
(
0,
f N
(1,
1)
−
1)
−
M
1,
−
f M N
(
−
1)
⎤
⎥
⎥
⎥
⎥
⎦
×
⎡
⎢
⎢
⎢
⎢
⎣
2
�
简写为
M fWWF =
N
,
式中, 的矩阵元为 ; 的矩阵元为 。
MW
ux
NW
vy
MW
NW
傅里叶逆变换矩阵式可如下获得
WfWWWf
=
1
−
M
M
N
1
−
N
=
FWW
1
−
M
1
−
N
。
易得(上式与二维离散傅里叶逆变换式对比)
W
1
−
M
=
1
M
⎡
W
⎢
W
⎢
⎢
W
⎢
⎢
M
⎢
W
⎢
⎣
0
M
0
M
0
M
0
M
易知
W
1
−
N
=
1
N
W
0
⎡
N
⎢
W
0
⎢
N
⎢
W
0
N
⎢
M
⎢
W
⎢
⎣
0
N
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
W
W
W
0
M
1
−
M
−
M
2
W
W
W
0
M
2
−
M
−
M
4
L
L
L
0
M
M
−
1)
2(
M
−
1)
W
(
−
M
−
M
W
W
M
M
(
−
1)
W
−
M
M
2 (
M
−
1)
W
−
M
M
M
(
2
−
1)
L
W
−
M
W
0
N
W
1
−
N
W
−
N
M
N
(
2
W
−
N
)1
−
W
0
N
W
2
−
N
W
−
N
M
(2
N
4
W
−
N
L
L
L
L
)1
−
0
N
N
W
(
−
N
(2
−
N
W
W
)1
−
N
)1
−
M
N
(
2)1
−
W
−
N
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
W
T
*
M
=
1
W
−
M
,
W
T
*
N
=
1
−
WN
,
故, 和 是酉矩阵,所对应的傅里叶变换是一种酉变换。
MW
NW
普遍情
况下,假如一个变换(或反变换)的变换核是可分离的,
均可写成
对
yxf
,(
)
⎧
⎨
⎩
x
y
=
=
方阵。
,2,1,0
,2,1,0
,
,
L
L
T
f
= AfB
1
−=
TBA
,
1
−
M
N
1
−
1
−
,矩阵 A 为
MM × 方阵;矩阵 B 为
NN ×
3
�
假如一个变换的变换核是不可分离的,有
T =
f
=
Af
TA
1−
,其中 A 和 1A−
均是
M × M
方阵,这时无法通过两次一维变换来实现二维变换。
2.2.2
One-D离散余弦变换(DCT)
[4,5]
DFT 供了频谱分析最重要的工具。但 DFT 运算是复数域运
提
算,
在实时处理中并不方便。
但傅立叶变换的实部只含有余弦项,可以构
造 DCT,这是一种实数域的变换,是简化傅里叶变换的重要方法,
在一系列视频压缩编码的国际标准建议中,都把|DCT 作为一个基本
处理模块,已经在图像压缩编码中得到广泛应用。
离散余弦变换的正变换核
xg
)0,(
=
uxg
),(
=
1
N
2
N
⎫
⎪⎪
(
⎬
u
)1
π
+
⎪
⎪⎭
N
2
2(
x
cos
对应的离散余弦变换
x
=
0,1,2,
L
,
N
u
1;-
=
,2,1
,
N
−
)1
L
F
)0(
=
uF
)(
= ∑
x
=
0
N
1
−
∑
x
N
=
0
1
−
1
N
2
N
xf
)(
(
x
=
,2,1,0
,
N
−
)1
L
2(
x
f
x
)(
cos
u
)1
+
π
N
2
u
(
=
,2,1
L
,
N
−
)1
其中 是时域 N 点序列; 为第 u 个余弦变换系数;u 为广义频
)(uF
)(xf
率变量。
取反变换核=正变换核,有
xf
)(
=
1
N
F
)0(
+
2
N
1
N
∑−
u
1
=
uF
)(
cos
2(
x
u
)1
+
π
N
2
(
x
=
,2,1,0
,
N
−
)1
L
4
�
2.2.3 Two-D 离散余弦变换
正变换
yxf
,(
)
=
F
)0,0(
F
v
),0(
uF
)0,(
=
vuF
),(
=
1
−
y
N
y
N
N
N
=
0
x
=
0
=
0
1
−
1
−
1
−
1
N
= ∑∑
∑∑
x
2
N
2
N
2
N
∑∑
∑∑
x
0
=
N
1
−
y
0
=
1
−
1
−
1
−
N
N
=
0
N
x
=
0
=
0
y
yxf
,(
)
cos
yxf
,(
)
cos
yxf
,(
)
cos
v
π
u
π
)1
)1
2(
y
+
N
2
x
2(
+
N
2
u
x
)1
+
π
N
2
2(
cos
2(
y
v
π
)1
+
N
2
其中,
yxf
,(
)
是空间域二维向量之元素,
yx
,
=
,2,1,0
L
,
N
−
1
;
vuF
),(
是
变换系数阵列之元素。式中表示的阵列为
NN × 。
2.2.4 正弦变换[1]
DST 的原始结果是由奇函数 ( ,
f x y 得到。可以如下定义变换核
)
A u x
( , )
=
2
+
1
N
sin
(
x
+
)
1
π
(
1)
N
u
+
+
1
x u
( ,
=
0,1,2,
,
N
-1)
L
One -D
对应的一维离散正弦变换与反变换公式分别为
F u
( )
=
f
x
( )
=
2
N
1
+
2
1
+
N
N
1
−
∑
x
=
N
0
1
−
∑
u
=
0
f x
( )sin
F u
( )sin
(
x
+
(
x
+
(
1)
N
(
1)
N
u
+
u
+
+
1
+
1
)
1
π
0
)
1
π
0
≤ ≤
u N
−
1
≤ ≤
x N
−
1
)(xf 是时域 N 点序列; )(uF 为第 u 个余弦变换系
数;u 为广义频
率变量。
Two-D
正变换与反变换分别为
5
�
F u
v
( , )
=
f x y
( ,
)
=
2
N
1
+
2
N
+
N
1
−
N
1
−
∑∑
x
=
0
y
=
0
N
1
−
1
−
N
∑∑
1 u
=
0
v
=
0
f x y
( ,
)sin
F u v
( , )sin
(
x
+
(
x
+
⎡
⎢
⎣
⎡
⎢
⎣
(
1)
N
(
1)
N
u
+
u
+
+
1
+
1
)
1
π
⎤
⎥
⎦
)
1
π
⎤
⎥
⎦
sin
sin
(
y
+
(
y
+
⎡
⎢
⎣
⎡
⎢
⎣
(
v
1)
N
+
(
v
1)
N
+
+
1
+
1
)
1
π
⎤
⎥
⎦
)
1
π
⎤
⎥
⎦
其中,
yxf
,(
)
是空间域二维向量之元素,
yx
,
=
,2,1,0
L
,
N
−
1
;
vuF
),(
是
变换系数阵列之元素。式中表示的阵列为
NN × 。
余弦变换与正弦变换的性质
1)
它们的正变换核与反变换核是相同的;
2) DCT 和 DST 分别是 DFT 的对称
和非
对称
扩展式;
3) DCT 和 DST 均有快速算
法;
4) DCT 和 DST 对图像均有把能量集中在低
频的特征。
关 这些性质的较详细讨论可以参
于
考教学参考书,如本章参考
文 中
献[1]
pp. 81- 83;参考文献[3]中pp. 83- 84。
Examp
le I To compute the discrete cosine transform for the autumn
i
mage.
RGB = imread('autumn.tif');
figure, imshow('autumn.tif');
I
= rgb2gray(RGB); % 将彩图转成灰度图像进行以进行
D
CT 变换
J = dct2(I);
figure, imshow(log(abs(J)),[]), colormap(jet(64)), colorbar
6
�
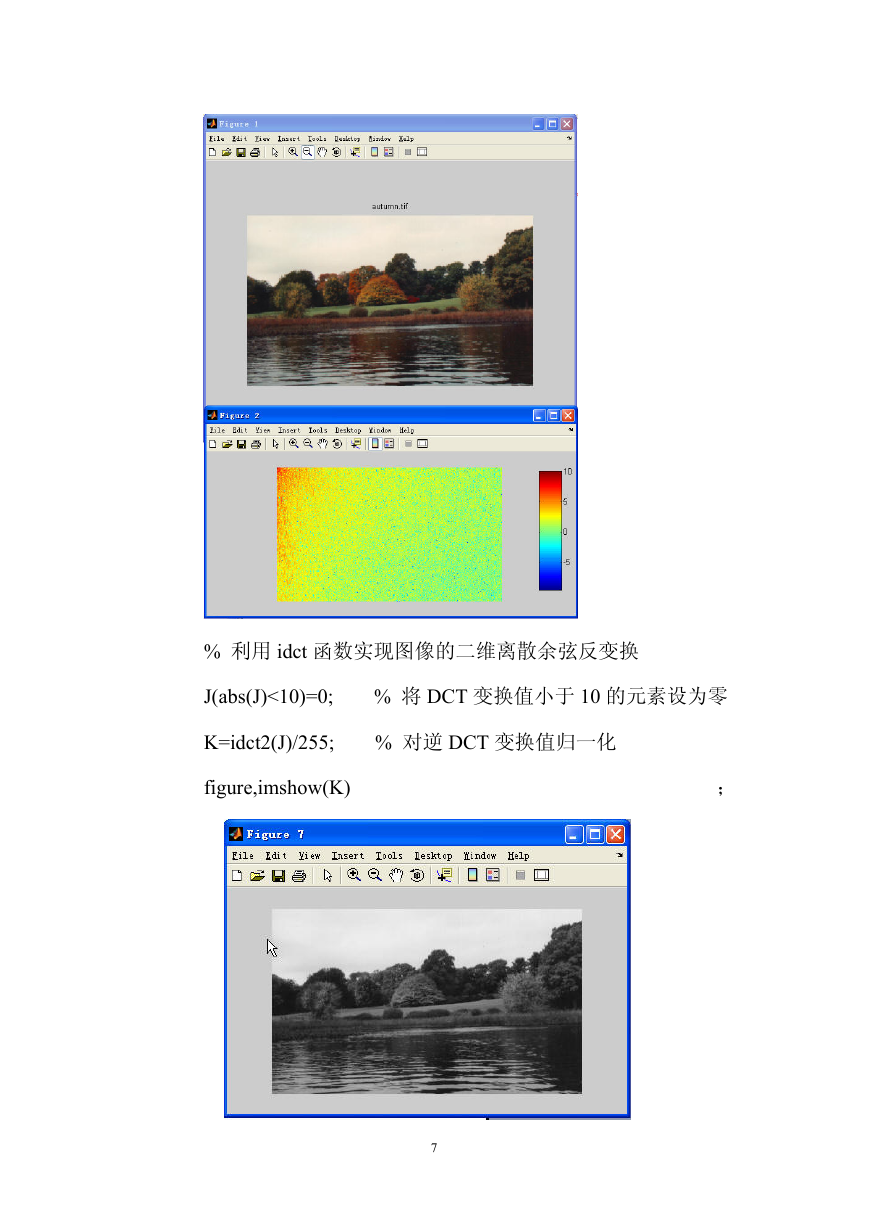
% 利用 idct 函数实现图像的二维离散余弦反变换
J(abs(J)<10)=0; % 将 DCT 变换值小于 10 的元素设为零
K=idct2(J)/255; % 对逆 DCT 变换值归一化
figure,imshow(K)
;
7
�













 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc