2008年广东省湛江市中考数学试题及答案.doc-资料库

第1页 / 共9页

第2页 / 共9页

第3页 / 共9页

第4页 / 共9页

第5页 / 共9页

第6页 / 共9页

第7页 / 共9页

第8页 / 共9页

2008 年广东省湛江市中考数学试题及答案说明：1．本试卷满分150 分，考试时间90 分钟． 2．本试卷共 4 页，共5 大题． 3．答题前，请认真阅读答题卡上的“注意事项”，然后按要求将答案写在答题卡相应的位置上． 4．请考生保持答题卡的整洁，考试结束，将试卷和答题卡一并交回．注意：在答题卡上作图必须用黑色字迹的钢笔或签字笔．一、选择题：本大题共 12 小题，每小题 3 分，共 36 分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．在 2 、0 、1、3 这四个数中比 0 小的数是（）Ａ． 2 Ｂ．0 Ｃ．1 D．3 2．人的大脑每天能记录大约8600 万条信息，数据8600 用科学计数法表示为（） A． 0.86 10 4 B． 8.6 10 2 C． 8.6 10 3 D． 86 10 2 3．不等式组Ａ． x   x      3 x 1 1 的解集为（）Ｂ． 3x  Ｃ． 1    3x D．无解 4． ⊙O的半径为5 ，圆心 O到直线l 的距离为3 ，则直线l 与⊙O的位置关系是（） A．相交 B．相切 C．相离 D．无法确定 5．下面的图形中，是中心对称图形的是（） A． B． C． D． 6．下列计算中，正确的是（） A． 2    2 B． 5  2  3 C． 3 a a  2  5 a D． 22x   x x 7．从 n 个苹果和3 个雪梨中，任选1个，若选中苹果的概率是 1 2 ，则 n 的值是（） A． 6 B． 3 C． 2 D． 1 8．函数 y  A． x  1  2 x 2 的自变量 x 的取值范围是（） B． x  2 C． x   2 D． x  2

9．数据 2 ， 7 ，3 ， 7 ，5 ，3 ， 7 的众数是（）Ａ． 2 Ｂ．3 Ｃ． 5 Ｄ． 7 10．将如图 1 所示的 Rt△ABC绕直角边 BC旋转一周，所得几何体的左视图是（） B C A 图 1 A B C D 11．已知三角形的面积一定，则它底边 a 上的高 h 与底边 a 之间的函数关系的图象大致是（） h O a h O a h O a h O a A． B． C． D ． 12．如图 2 所示，已知等边三角形 ABC的边长为1，按图中所示的规律，用 2008 个这样的三角形镶嵌而成的四边形的周长是（） A B C Ａ． 2008 Ｂ． 2009 必须是偶数而且长度比个数多 2 ┅┅ 图 2 Ｃ． 2010 Ｄ． 2011 二、填空题：本大题共 6 小题，每小题 4 分，共 24 分． 13．湛江市某天的最高气温是 27 ℃，最低气温是17 ℃，那么当天的温差是 10 ℃． 14．分解因式： 22 a  2 ab  2a（a-b）． 15．圆柱的底面周长为 2，高为3 ，则圆柱侧面展开图的面积是 6 派 16．如图 3 所示，请写出能判定 CE∥AB的一个条件角 ecb=角 cba ．． D C A 图 3 E B 海洋 71% 陆地 29% 图 4 17．图 4 所示的扇形图给出的是地球上海洋、陆地的表面积约占地球总表面积的百分比，若宇宙中有一块陨石落在地球上，则它落在海洋中的概率是 71% ． 18．将正整数按如图 5 所示的规律排列下去，若有序实数对（ n ， m ）表示第 n 排，从左

到右第 m 个数，如（ 4 ，2 ）表示实数9 ，则表示实数17 的有序实数对是（6，2）． 3 9 4 10 1 5 2 8 ┅┅ 6 7 图 5 第一排第二排第三排第四排三、解答题：本大题共 5 小题，每小题 7 分，共 35 分． 19．计算：( 1 )2008－(－3 )0＋ 4 ． =2 20．某足球比赛的计分规则为胜一场得3 分，平一场得1分，负一场得 0 分．一个队踢14 场球负5 场共得19 分，问这个队胜了几场？ =5 14—5=9 场（赢或者平）设球队赢 x 场，平 y 场 3x+y=19 x+y=9 解方程 x=5 y=4 答： 21．有五张除字不同其余都相同的卡片分别放在甲、乙两盒子中，已知甲盒子有三张，分别写有“北”、“京”、“奥”字样，乙盒子有两张，分别写有“运”、“会”字样，若依次从甲乙两盒子中各取一张卡片，求能拼成“奥运”两字的概率．三分之一 x 二分之一=六分之一 22．如图 6 所示，课外活动中，小明在离旗杆 AB 10 米的 C处，用测角仪测得旗杆顶部 A 的仰角为 40 ，已知测角仪器的高 CD=1.5 米，求旗杆 AB的高． (精确到 0.1 米) （供选用的数据： sin 40  0.64 ， cos 40  0.77 ， tan 40  0.84 ）由题可知 de=cb=10 米在三角形 aed 中，天剑 40 度=ae 除以 de=0.84 求得 ae=8.4 米由图可知旗杆 ab=ae+be 而 cd=be=1.5 米所以旗杆 ab=ae+be=8.4+1.5=9.9 米答 D C 40 图 6 A E B

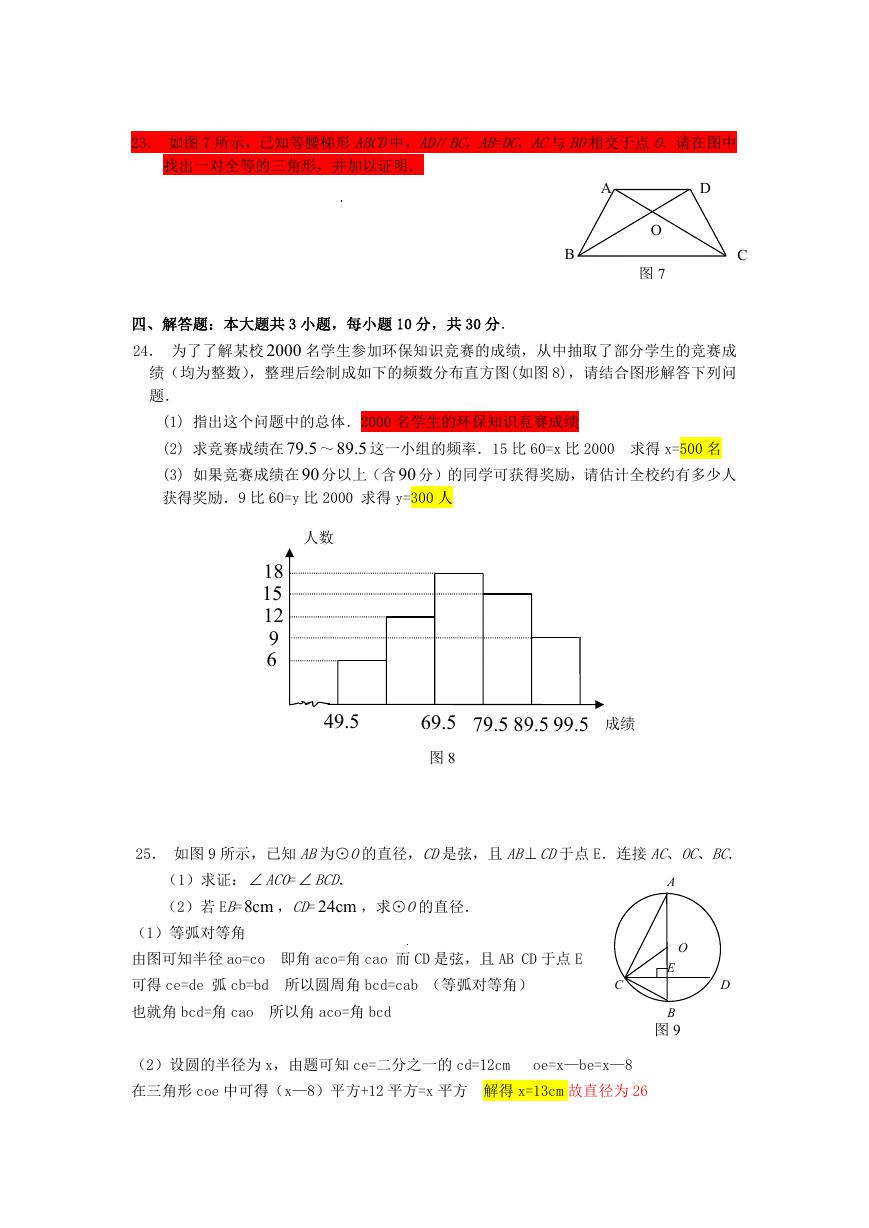
23．如图 7 所示，已知等腰梯形 ABCD中，AD∥BC，AB=DC，AC与 BD相交于点 O．请在图中找出一对全等的三角形，并加以证明． A D B O 图 7 C 四、解答题：本大题共 3 小题，每小题 10 分，共 30 分． 24．为了了解某校 2000 名学生参加环保知识竞赛的成绩，从中抽取了部分学生的竞赛成绩（均为整数），整理后绘制成如下的频数分布直方图(如图 8)，请结合图形解答下列问题． (1) 指出这个问题中的总体．2000 名学生的环保知识竞赛成绩 (2) 求竞赛成绩在 79.5 ～89.5 这一小组的频率．15 比 60=x 比 2000 求得 x=500 名 (3) 如果竞赛成绩在90 分以上（含90 分）的同学可获得奖励，请估计全校约有多少人获得奖励．9 比 60=y 比 2000 求得 y=300 人人数 18 15 12 9 6 49.5 69.5 图 8 79.5 89.5 99.5 成绩 25．如图 9 所示，已知 AB为⊙O的直径，CD是弦，且 AB CD于点 E．连接 AC、OC、BC．（1）求证：  ACO=  BCD．（2）若 EB=8cm ，CD= 24cm ，求⊙O的直径．（1）等弧对等角由图可知半径 ao=co 即角 aco=角 cao 而 CD 是弦，且 AB CD 于点 E A O E 可得 ce=de 弧 cb=bd 所以圆周角 bcd=cab （等弧对等角） C D 也就角 bcd=角 cao 所以角 aco=角 bcd B 图 9 （2）设圆的半径为 x，由题可知 ce=二分之一的 cd=12cm oe=x—be=x—8 在三角形 coe 中可得（x—8）平方+12 平方=x 平方解得 x=13cm 故直径为 26

26．某农户种植一种经济作物，总用水量 y （米 3 ）与种植时间 x （天）之间的函数关系式如图 10 所示． y（米 3 ）（1）第 20 天的总用水量为多少米 3 ？1000 （2）当 x  20 时，求 y 与 x 之间的函数关系式．（3）种植时间为多少天时，总用水量达到 7000 米 3 ？ 4000 1000 O 设 y=kx+b 方程组 1000=20k+b 和 4000=30k+b 求得 k=300 b=—5000 所以 y=300x—5000 将 y=7000 代入函数关系式可得 x=40 答：40 天。。。。。。。。。。 20 30 x (天) 图 10 五、解答题：本大题共 2 小题，其中第 27 题 12 分，28 题 13 分，共 25 分． 27．先观察下列等式，然后用你发现的规律解答下列问题．   11   2 1 1 2 3 1 1 3 4   1 1 2  1 2 3  1 3 4  ┅┅ 1 1 2  1 1 2  (1) 计算（2）探究    1 1 2 3 3 4   1 1 2 3 3 4     1 4 5   ......   1 5 6  1 ( n n  1)  六分之五．  （n+1 ）分之 n ．（用含有 n 的式子表示）（3）若 1 1 1 3 3 5     1 5 7   ......  1 1)(2 n  1) (2 n  的值为 17 35 ，求 n 的值． 28．如图 11 所示，已知抛物线 y x 2 1  与 x 轴交于 A、B两点，与 y 轴交于点 C．

（1）求 A、B、C三点的坐标．（2）过点 A作 AP∥CB交抛物线于点 P，求四边形 ACBP的面积．（3）在 x 轴上方的抛物线上是否存在一点 M，过 M作 MG x 轴于点 G，使以 A、M、G三点为顶点的三角形与  PCA相似．若存在，请求出 M点的坐标；否则，请说明理由． A（1，0） B（—1，0） C（0，—1） 4 数学试题参考答案及评分标准一、选择题：本大题共 12 小题，每小题 3 分，共 36 分． 1． A 3． C 6． C 4． A 2． C 5． D 7． B y P A o C B x 图 11 8． B 9． D 10． A 11 D 12． C 二、填空题：本大题共 6 小题，每小题 4 分，共 24 分． 13 ． 10 18．（，） 14 ． 15 ． 16 ． DCE= A 或 ECB= B 或 A+ ACE= 17．三、解答题：本大题共 5 小题，每小题 7 分，共 35 分． 19．解：原式= = 20．解：设这个队胜了场，依题意得: （分）（分）（分）（分）解得：答：这个队胜了场．（分） 21．解：由题意可得：乙盒运（北，运）（京，运）（奥，运）会（北，会）（京，会）（奥，会）北京奥甲盒（4 分）从表中可以看出，依次从甲乙两盒子中各取一张卡片，可能出现的结果．有个，它们出现的可能性相等，其中能拼成 “ 奥运 ” 两字的结果有个．（5 分）所以能拼成“奥运”两字的概率为．（分） 22．解：在 Rt△ADE 中， ADE= （2 分） ∵DE= ， ADE= ∴AE=DE ADE = ≈ = （4 分） ∴AB=AE+EB=AE+DC= （6 分）

答：旗杆 AB 的高为米．（7 分） 23．解： ABC≌ DCB （2 分）证明：∵在等腰梯形 ABCD 中，AD∥BC，AB=DC ∴ ABC= DCB （4 分）在 ABC 与 DCB 中 ∴ ABC≌ DCB （7 分）（注：答案不唯一）四、解答题：本大题共 3 小题，每小题 10 分，共 30 分． 24．解： (1) 总体是某校名学生参加环保知识竞赛的成绩．（2 分）（2）（5 分）答：竞赛成绩在～这一小组的频率为．（6 分）（3）（9 分）答：估计全校约有人获得奖励．（10 分）（2 分）（3 分） 25．证明：(1)∵AB 为⊙O 的直径，CD 是弦，且 AB CD 于 E， ∴CE=ED， ∴ BCD= BAC ∵OA=OC ∴ OAC= OCA ∴ ACO= BCD （5 分） (2)设⊙O 的半径为 Rcm，则 OE=OB EB=R 8 CE= CD= 在 Rt CEO 中，由勾股定理可得 OC =OE +CE 解得 R=13 答：⊙O 的直径为 26cm．（10 分） 26．解：（1）第天的总用水量为米（3 分）即 R = (R 8) ∴2R=2 13=26 +12 （8 分） (6 分） 24=12 （2）当时，设 ∵函数图象经过点（20，1000），（30，4000） ∴ （5 分）解得 ∴ 与之间的函数关系式为：y=300 （3）当 y =7000 时有 7000=300 5000 解得 =40 5000 （7 分）答：种植时间为 40 天时，总用水量达到 7000 米（10 分）（3 分）五、解答题：本大题共 2 小题，其中第 27 题 12 分，28 题 13 分，共 25 分． 27．解：（1）（2）（6 分）（3） = + ┄ + = = 由 = （11 分）经检验是方程的根，∴ （12 分） 28．解：（1）令，得（9 分）解得解得

B 令，得 ∴ A （2）∵OA=OB=OC= ∵AP∥CB， C （2 分） ∴ BAC= ACO= BCO= ∴ PAB= 过点 P 作 PE 轴于 E，则 APE 为等腰直角三角形令 OE= ，则 PE= ∴P ∵点 P 在抛物线上 ∴ 解得，（不合题意，舍去） ∴PE= 4 分） 6 分） 7 分） ∴PA AC PCA 时，有 = ∴AC= ∴AP= ∴四边形 ACBP 的面积 = AB•OC+ AB•PE = (3)．假设存在 ∵ PAB= BAC = ∵MG 轴于点 G， ∴ MGA= PAC = 在 Rt△AOC 中，OA=OC= 在 Rt△PAE 中，AE=PE= 设 M 点的横坐标为，则 M ①点 M 在轴左侧时，则 (ⅰ) 当 AMG ∵AG= ，MG= 即解得（舍去）（舍去） (ⅱ) 当 MAG PCA 时有 = 即解得：（舍去） ∴M ② 点 M 在轴右侧时，则 (ⅰ) 当 AMG ∵AG= ，MG= ∴ 解得（舍去）（10 分） PCA 时有 = ∴M PCA 时有 = (ⅱ) 当 MAG 即解得：（舍去） ∴M ∴存在点 M，使以 A、M、G 三点为顶点的三角形与 PCA 相似 M 点的坐标为，，（13 分）说明：以上各题如有其他解（证）法，请酌情给分沁园春·雪北国风光，千里冰封，万里雪飘。

资料库

2008年广东省湛江市中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料