第29卷第8期 2007年8月 系统工程与电子技术 Systems Engineering and Electronics V01．29 No．8 Aug．2007 文章编号：1001—506X(2007)08—1238～04 基于自适应窗的小波域图像去噪算法 周祚峰，水鹏朗，李军侠 (西安电子科技大学雷达信号处理国家重点实验室，陕西西安710071) 摘 要：提出了一种利用自适应窗的小渡域双重局部维纳滤波图像去噪算法。综合考虑小波分解后各 个子带中能量分布的方向特性和图像本身的边缘和纹理特性，该算法首先估计每个子带中信号的能量分布 进而在每个子带中确定自适应窗，然后利用自适应窗估计出的能量分布对含噪图像进行双重维纳滤波来去 除噪声。实验结果表明该算法对含噪图像去噪的效果优于已有的采用二雏可分实小波进行图像去噪的 算法。 关键词：双重局部维纳滤波；自适应窗；小波去噪；能量分布 中图分类号：TN 973．3 文献标志码：A Image denoising algorithm based on adaptive windows in wavelet domain ZHOU Zuo—feng，SHUI Peng—lang，LI Jun-xia (Key Lab．ofRadar Signal Processing，Xidian Univ．，Xi’an 710071，China) Abstract：The image denoising algorithm based on wavelet analysis is a hot point in image processing appli— cations．A wavelet—based image denoising algorithm via doubly local Wiener filtering with adaptive windows is presented．Combing the consideration of the energy distributions’directional features of each subband after wavelet decomposition and the intrinsic features of the edge and textures of natural images，firstly，the adaptive windows are fixed by autocorrelation function of wavelet coefficients’energy distribution，and then the doubly local Wiener filtering is used to denoise the noisy image．Experiment results show that the proposed algorithm is better than the existing image denoising algorithms using the separable 2-D real wavelets． Keywords：doubly local Wiener filtering；adaptive window；wavelet denoising；energy distribution 0 引 言 系数来估计信号的方差。文献[6～7]中，不只利用待估计 点的同子带内邻域中的系数，还要加上下一个较粗尺度上 近年来，基于小波的图像去噪算法在图像处理应用中 相同位置的小波系数来估计该点的信号方差。 发挥了重要的作用。在这些算法中，空间自适应方法可以 上述的大部分算法一般假定图像在小波域中的3个方 达到很好的效果并且计算复杂度较低。图像的小波域系数 向子带中的能量分布是各向同性的，窗的选择并没有考虑 可以认为是方差随空间位置变化的条件独立高斯随机变 各子带的方向选择性。大多数实际图像在小波分解后的不 量。空间自适应方法中关键的一步就是如何准确地估计信 同方向子带内能量分布显示出不同的方向特性，文献[1]中 号在每个子带中的方差或能量分布。基于小波域中不同尺 考虑了小波分解后子带中能量分布所具有这种方向选择 度和同尺度间信号能量分布的强相关性，一些方法利用含 性，提出了一种匹配于子带滤波器方向选择性的椭圆形方 噪环境下待估计点适当邻域内的小波系数来估计这一点的 向窗。然而，图像在小波域各子带中的能量分布并不单纯 信号方差，即在待估计点的邻域建立一个窗，利用窗内的系 由子带的方向选择性决定的，它还跟图像本身的边缘以及 数来估计该点的方差。文献[23中，基于区域融合思想，子 纹理的方向分布有关。本文中，我们兼顾子带的方向选择 带中每～点信号的方差是用一个由一些小正方形窗组合起 性和图像本身的边缘和纹理特征，利用计算小波域系数能 来的几乎任意形状的窗来估计的。文献[3]中，首先对窗内 量分布的自相关函数来确定自适应窗，然后通过双重局部 的含噪小波系数进行阈值处理，然后再用窗内的剩余小波 维纳滤波对含噪图像进行去噪。 收稿日期：2006—07—12；修回日期：2007—02—12。 基金项目：国家自然科学基金(60472086)；博士点基金(20050701014)资助课题 作者简介：周祚峰(1982一)，男，博士研究生，主要研究方向为多速率滤波器组理论，小波理论及其在图像处理中的应用。 @126．con ˝ • ‰ ˚ 

第8期 周祚峰等：基于自适应窗的小波域图像去噪算法 · 1239 · 1双重局部维纳滤波 信号的方差是通过含噪信号的小波域系数来估计的，我们 选用短支撑的小波基，这样可以使图像边缘的能量在小波 假定一幅图像被加性的均值为0，方差为蠢的高斯白 域尽可能地集中以便在去噪中能更好地保留边缘；而在第 噪声污染，则含噪图像在小波域可以表示为 二次局部维纳滤波中，估计信号方差时选用的引导图像含 y(i，j)=s(i，j)+e(i，j) (1) 有较少的噪声，我们更倾向于选择高消失矩的小波基，这样 式中，s(i，j)为真实图像的小波系数；￡(i，J)为噪声的小波 就可以更好地保持图像的光滑性。 系数。使用正交小波变换时，e(i，j)也是服从零均值，方差 为蠢的独立同分布的高斯型随机变量。这里为了简单起 2自适应窗的选取 见，略去了不同尺度及不同子带间的下标。 传统的采用正方形窗去噪的算法是假定窗中所有的点 含噪图像在小波域的局部维纳滤波主要由两部分组 和待估计点具有很强的相关性，可以近似地认为是服从同 成。首先每一点信号的方差孑(i，j)由以它为中心的一个 一种分布，所以对所有的点都同等对待，即求得窗中所有点 窗中的所有含噪图像小波分解系数的平均得到，即 的方差后取平均得到待估计点方差的一个估计。但这种假 ；2(i，j)一(雨茜。磊∥2(i+p，j+g)一《)+(2) 式中：(z)+一max(0，z)，W和#W分别为窗和窗中点的 定是不太合理的，窗中有些点的方差很可能与待估计点的 方差有较大的差别。 采用方向窗的图像去噪算法[13考虑了能量分布在子带 个数。接着通过对含噪图像小波域系数的局部维纳滤波来 中的方向性，选取了具有方向性的椭圆型窗函数，实际上是 估计信号的小波系数，即 s(i，j)_蠢势‰y。，j) 把正方形窗中那些不在特定方向上的点去掉了一部分，使 (3) 剩下的那些点的方差更接近于待估计点的方差，所以对去 噪的效果有了一定的改善。图2给出了常用的“Barbara” 图1给出了本文算法的框图表示。我们首先用第一个 小波基对含噪图像进行小波分解，并在各个子带中估计出 自适应窗，接着使用基于自适应窗的局部维纳滤波对含噪 图像去除一次噪声得到一幅近似“干净”的图像，我们把它 称为引导图像。然后用第二个小波基对引导图像进行小波 分解，使用自适应窗来得到对信号方差的一个估计，不同的 是这次信号的方差是通过引导图像的小波域系数来估计 的，即 图像在采用‘sym8’小波进行五层非下采样小波分解后第 三层上的信号能量分布情况。由图2可以看出，各个子带 中的能量分布显示出明显的匹配于子带滤波器方向选择性 的方向特性。但是基于椭圆形方向窗的去噪算法没有考虑 图像本身的几何特征对子带中能量分布的影响。如果一幅 图像本身沿水平方向的边缘很少，那么图像在小波域的水 平高频子带中沿着水平方向的能量分布也就很少，如果继 续采用沿水平方向上的椭圆形方向窗进行去噪作用就不 ≯“，j)-赢。，要，；2“+蛳+q) (4) 明显。 式中，W。和s(i，j)分别代表自适应窗和引导图像在第二个 小波基下的分解系数，接着对含噪图像在第二个小波域再 进行一次局部维纳滤波从而得到最终的去噪结果，则第二 次局部维纳滤波就可以表示为 s-幻)-纛芳‰Y 2Q∽ (5) 式中：Y。(i，j)为含噪图像在第二个小波基分解下的小波域 系数。该算法称为基于自适应窗的小波域双重局部维纳滤 波图像去噪算法。甲一匝垂卜臣黼部陋萼四 圈 2—— I 区圆 匾画亟}咂匪匦亟蟹圃—巫图 』匝壹i歪2卜E囹Iit I小波逆变换rl 去噪像I L______-____·____J。’。。。。。。。。。’’。。。。一 l J 图2各个子带中的能量分布 在小波域中，由图像的边缘或纹理区域引起的幅值大 的小波系数通常会聚集在一起形成能量簇，这些能量簇包 含了信号的大部分能量和边缘信息。子带中能量簇的主方 向是由边缘的方向和子带滤波器的方向选择性共同决定 的。我们采用计算能量分布的自相关函数来确定子带中的 能量簇分布情况，在能量分布的自相关函数取值大的那些 点聚集的方向就是子带中能量分布的方向，这样既考虑到 子带滤波器的方向选择性，又兼顾了图像本身的边缘和纹 图1本文算法的框图表示 理特性。然后窗的方向就取为能量簇分布的主方向，在子 在小波基的选取问题上，第一次局部维纳滤波中，由于 带中实现了窗的自适应选择。具体步骤如下： 假设s(i，j)是图像经过小波分解后子带中的小波系 ˝ • ‰ ˚ 

·1240· 系统工程与电子技术 第29卷 数。首先计算子带的能量分布自相关函数 层数依次取为(80，70，60，50，40)；在第二重局部维纳滤波 r(矗，z)一1只；2(m，挖)；2(m+惫，n+z) 定义权重矩阵 p(曼，z)一_：型兰∑； ~／1+A(舻+z2) (6) (7) 通过增大参数A，可以降低离待估计点远的点对待估计点的 影响。 设p-(·)是把p(k，z)从大到小排序后所得到的结果， 则自适应窗中的点就可以选取为ID’(·)中前M个点，即 p(k，Z)中系数最大的那M个点 W。{(愚，Z)：p(h，Z)≥p’(M)) (8) 式中，阢为自适应窗。图3给出了按照以上方法对图2中 各个子带做处理所得到的几种自适应窗。 n u 几u 中采用“sym8”小波对图像进行分解，自适应窗中点的个数 M按层数依次取为(25，20，15，10，5)；权重系数矩阵中A取 为0．2。实验结果表明A的取值大小对去噪结果的影响不 大。考虑到噪声样本的随机性，对每一个输入信噪比，输 出的峰值信噪比表示取50次不同噪声样本下输出峰值信 噪比的平均值。图4给出了Lena图像被盯一20的高斯白 噪声污染后采用几种最大下采样算法去噪的局部效果比 较，由图4可以看出本文算法可以更好地去除噪声，同时 保留图像的边缘信息。输出峰值信噪比结果如表1。由 表1可以看出，在文献[1]算法的基础上，本文算法在计算 复杂度方面只是多了一个计算子带中能量分布的自相关 函数的计算量，但是本文所提出的算法在去噪效果上比最 近文献[1]中提出的算法峰值信噪比又提高了o．2 dB，在 目前用最大下采样二维可分实小波去噪的算法中效果是 最好的。 图3自适应窗 3 实验结果 我们选常用的Lena和Barbara图像作为测试图像。对 其做5层的二维可分离小波分解，边界采用对称延拓方式。 在小波图像去噪中，噪声的方差一般可以通过对第一层对 角子带上的小波分解系数进行绝对中值估计而比较精确的 得到，同文献[1，9]等，本文假设噪声方差也是已知的。 在采用最大下采样小波分解情况下，同文献[1]中小波 基和窗的尺寸的选取方法，第一重局部维纳滤波中我们采 用“db4”小波对图像进行分解，自适应窗中点的个数M按 图4 去噪效果比较 表1量大下采样情况下各种算法的去噪效果比较 lena barbara 在非下采样小波分解情况下，我们仍选用“db4”和 应当随着分解层数的增加而增大，试验中第一次维纳滤波 “sym8”分别作为对图像进行第一重分解和第二重分解时 中M的取值依次为(171，191，211，231，251)，第二次维纳 所选用的小波基。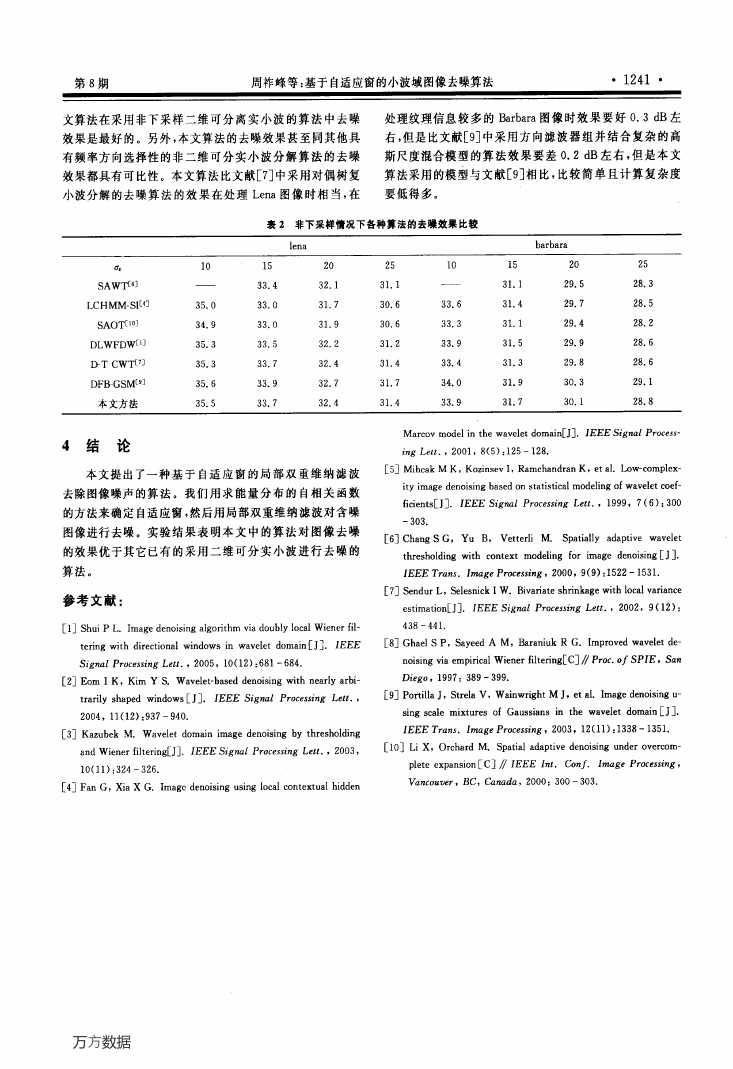但随着非下采样小波分解层数的增加， 滤波中M的取值依次为(61，71，81，91，101)，A的选取同 能量簇被逐渐的平滑，此时自适应窗中的点数M的取值 下采样情况。试验结果如表2。由实验结果可以看出：本 ˝ • ‰ ˚ 

第8期 周祚峰等：基于自适应窗的小波域图像去噪算法 ·1241· 文算法在采用非下采样二维可分离实小波的算法中去噪 效果是最好的。另外，本文算法的去噪效果甚至同其他具 处理纹理信息较多的Barbara图像时效果要好0．3 dB左 右，但是比文献[9]中采用方向滤波器组并结合复杂的高 有频率方向选择性的非二维可分实小波分解算法的去噪 斯尺度混合模型的算法效果要差0．2 dB左右，但是本文 效果都具有可比性。本文算法比文献[7]中采用对偶树复 算法采用的模型与文献[9]相比，比较简单且计算复杂度 小波分解的去噪算法的效果在处理Lena图像时相当，在 要低得多。 表2非下采样情况下各种算法的去噪效果比较 4 结 论 本文提出了一种基于自适应窗的局部双重维纳滤波 去除图像噪声的算法。我们用求能量分布的自相关函数 的方法来确定自适应窗，然后用局部双重维纳滤波对含噪 图像进行去噪。实验结果表明本文中的算法对图像去噪 的效果优于其它已有的采用二维可分实小波进行去噪的 算法。 参考文献： Marcov model in the wavelet domain[J]．IEEE Signal Process— ing Lett．，2001，8(5)：125—128． [5]Miheak M K，Kozinsev I，Ramchandran K，et a1．Low—complex— ity image denoising based on statistical modeling of wavelet coef— ficients[J]．IEEE Signal Processing Lett．，1999，7(6)：300 —303． [6]Chang S G，Yu B，Vetterli M．Spatially adaptive wavelet thresholding with context modeling for image denoising[J]． IEEETrans．ImageProcessing，2000，9(9)：1522—1531． [7]Sendur L，Selesnick I W．Bivariate shrinkage with local variance estimation[J]．IEEE Signal Processing Lett．，2002，9(12)： [1]Shui P L．Image denoising algorithm via doubly local Wiener fil— 438～441． tering with directional windows in wavelet domain[J]．IEEE [8]Ghael S P，Sayeed A M，Baraniuk R G．Improved wavelet de— Signal Processing Lett．，2005，10(12)：681—684． noising via empirical Wiener filtering[C]{}Proc．of SPIE．San [2]Eom I K，Kim Y S．Wavelet-based denoising with nearly arbi- Diego，1997：389—399． trarily shaped windows[J]．IEEE Signal Processing Lett．， 2004，11(12)：937—940． [9]Portilla J，Strela V，Wainwright M J，et a1．Image denoising U— sing scale mixtures of Gaussians in the wavelet domain[J]． [3]Kazubek M．Wavelet domain image denoising by thresholding IEEETram．ImageProcessing，2003，12(11)：1338—1351． and Wiener filtering[J]．IEEE Signal Processing Lett．，2003， 10(11)：324—326． [10]Li X，Orchard M．Spatial adaptive denoising under overcom— plete expansion[c]∥IEEE Int．Conf．Image Processing， [4]Fan G，Xia X G．Image denoising using local contextual hidden Vancouver，BC，Canada，2000：300～303． ˝ • ‰ ˚