第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
模糊聚类分析matlab.doc
设论域为被分类对
于是，得到原始数据矩阵为
，
显然有，而且也消除了量纲的影响。
（2）最大值规格化：
2.5.1根据所求得的传递闭包，再让由大变小，
专业：信息与计算科学 姓名： 学号：
实验一 模糊聚类分析
实验目的：
掌握数据文件的标准化，模糊相似矩阵的建立方法，会求传递闭包矩阵；会
使用数学软件 MATLAB 进行模糊矩阵的有关运算
实验学时：4 学时
实验内容：
⑴ 根据已知数据进行数据标准化.
⑵ 根据已知数据建立模糊相似矩阵，并求出其传递闭包矩阵.
⑶ (可选做)根据模糊等价矩阵绘制动态聚类图.
⑷ (可选做)根据原始数据或标准化后的数据和⑶的结果确定最佳分类.
实验日期：20017 年 12 月 02 日
实验步骤：
1 问题描述：
设有 8 种产品，它们的指标如下：
x1 = (37,38,12,16,13,12)
x2 = (69,73,74,22,64,17)
x3 = (73,86,49,27,68,39)
x4 = (57,58,64,84,63,28)
x5 = (38,56,65,85,62,27)
x6 = (65,55,64,15,26,48)
x7 = (65,56,15,42,65,35)
x8 = (66,45,65,55,34,32)
建立相似矩阵，并用传递闭包法进行模糊聚类。
2 解决步骤：
2.1 建立原始数据矩阵
}
,
,2,1
X
设论域
,
,
x
1
i
,{
xx
1
2
im
x
i
，
nx
x
i
x
i
2
,
为被分类对象，每个对象又有 m 个指标表示其性状，
,
由此可得原始数据矩阵。
n
于是，得到原始数据矩阵为
X
37
69
73
57
38
65
65
66
38
73
86
58
56
55
56
45
12
74
49
64
65
64
15
65
16
22
27
84
85
15
42
55
13
64
68
63
62
26
65
34
12
17
39
28
27
48
35
32
其中 nmx 表示第 n 个分类对象的第 m 个指标的原始数据，其中 m = 6，n = 8。
2.2 样本数据标准化
2.2.1 对上述矩阵进行如下变化，将数据压缩到[0,1]，使用方法为平移极差
变换和最大值规格化方法。
（1）平移极差变换：
x
ik
x
ik
min{ }
x
ik
1
i n
max{ } min{ }
x
ik
1
i n
x
ik
1
i n
， (
k
1,2,
,
m
)
显然有 0
ikx
1
，而且也消除了量纲的影响。
（2）最大值规格化：
x
ij
x '
ij M
j
，
M
max(
x
1
j
,
x
2
j
,
x
nj
)
j
2.2.2 使用 Matlab 实现代码：
function [x_zuida, x_pingyi] = bzh(x)
%函数功能：标准化矩阵
[m,n] = size(x);
B = max(x);
B1 = max(x) - min(x);
Bm = min(x);
for i = 1:n
x1(:,i) = x(:,i)/B(i); %最大值规格化
x2(:,i) = (x(:,i) - Bm(i))/B1(i); %平移极差标准
化
end
x_zuida = x1
x_pingyi = x2
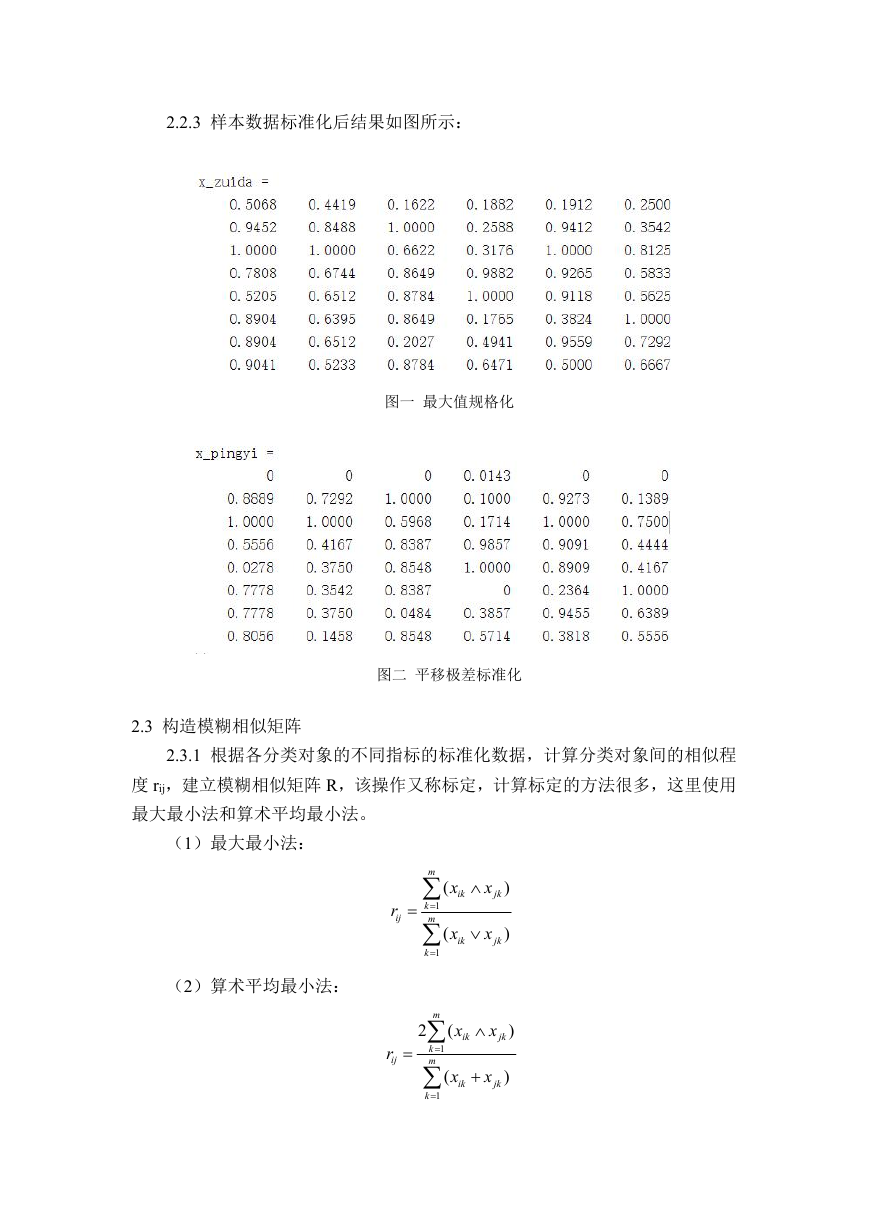
2.2.3 样本数据标准化后结果如图所示：
图一 最大值规格化
图二 平移极差标准化
2.3 构造模糊相似矩阵
2.3.1 根据各分类对象的不同指标的标准化数据，计算分类对象间的相似程
度 rij，建立模糊相似矩阵 R，该操作又称标定，计算标定的方法很多，这里使用
最大最小法和算术平均最小法。
（1）最大最小法：
（2）算术平均最小法：
r
ij
r
ij
m
1
k
m
k
1
(
x
ik
x
jk
(
x
ik
x
jk
)
)
m
2
1
k
m
(
k
1
(
x
ik
x
)
jk
x
ik
x
)
jk
2.3.2 使用 Matlab 实现代码：
function [R1,R2] = bd(x)
%函数功能：标定
[m,n] = size(x);
for i = 1:m
for j = 1:m
for k = 1:n
qx(k) = min(x(i,k),x(j,k)); %取小
qd(k) = max(x(i,k),x(j,k)); %取大
end
R1(i,j) = sum(qx)/sum(qd); %最大最小法
R2(i,j) = 2*sum(qx)/(sum(x(i,:))+sum(x(j,:))); %算术平均
最小法
if i == j
R1(i,j) = 1;
R2(i,j) = 1;
end
end
end
R_zuidazuixiao = R1
R_suanshu = R2
2.3.4 将最大规格化后的数据进行构造模糊相似矩阵如图所示：
图三 最大最小法构造模糊相似矩阵
图四 算术平均法造构造模糊相似矩阵
2.4 建立模糊等价矩阵
2.4.1 根据标定所得的矩阵，只是一个模糊相似矩阵 R ，不一定具有传递性，
为了进行分类，还需要将 R 改造成等价矩阵 *R 。采用平方法计算传递闭包：
R
经过有限次运算后存在 k 使
R
R
2
kR
)1
，于是
R
4
R
k R
(2
k
2
2
* ， *R 即为所求的模
2
kR
糊等价矩阵。
2.4.2 使用 Matlab 实现代码：
function [tr] = chuandi(x)
%函数功能：求传递闭包
R = x;
a=size(R);
B=zeros(a);
flag=0;
while flag==0
for i= 1: a
for j= 1: a
for k=1:a
B( i , j ) = max(min( R( i , k) , R( k, j) ) , B( i , j ) ) ;%R 与 R
内积，先取小再取大
end
end
end
if B==R
flag=1;
R=B;%循环计算 R 传递闭包
else
end
end
tr = B;
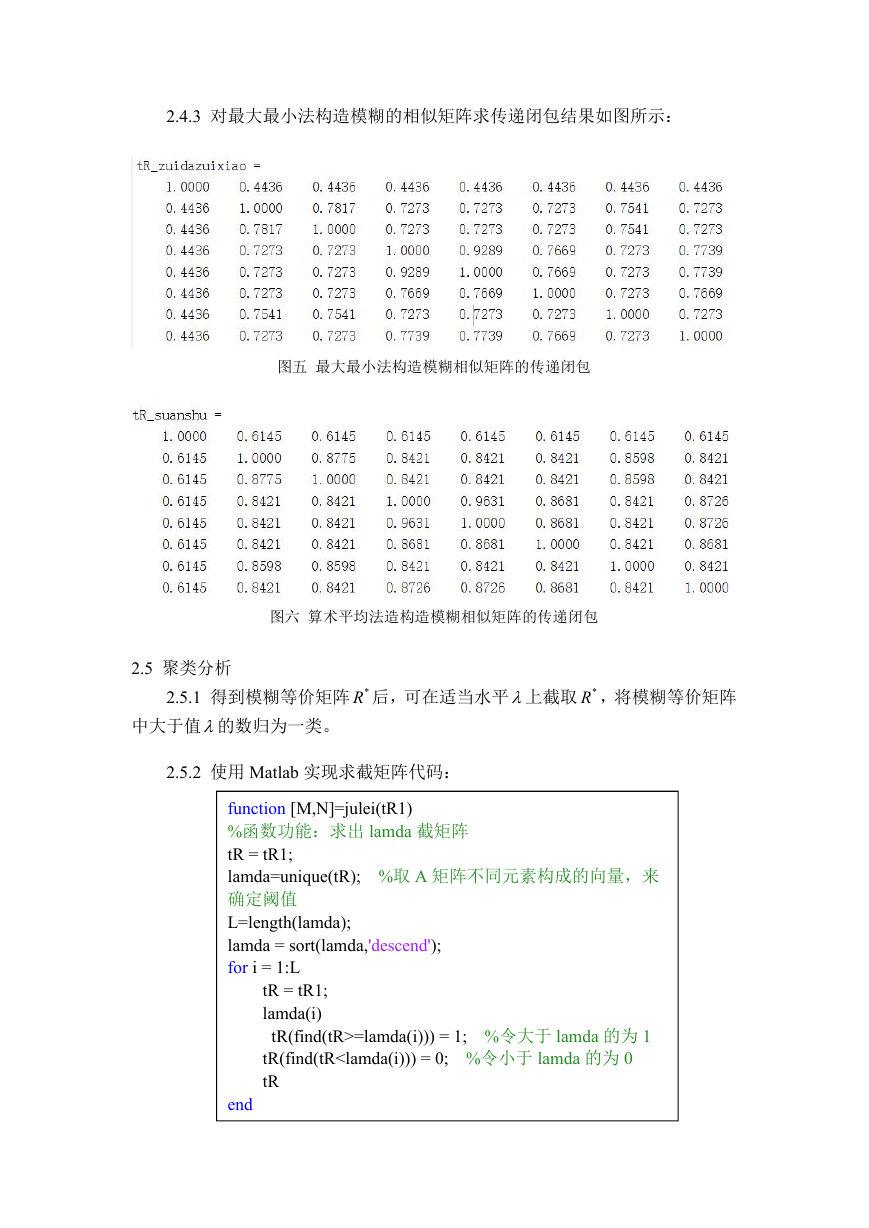
2.4.3 对最大最小法构造模糊的相似矩阵求传递闭包结果如图所示：
图五 最大最小法构造模糊相似矩阵的传递闭包
图六 算术平均法造构造模糊相似矩阵的传递闭包
2.5 聚类分析
2.5.1 得到模糊等价矩阵 *R 后，可在适当水平上截取 *R ，将模糊等价矩阵
中大于值的数归为一类。
2.5.2 使用 Matlab 实现求截矩阵代码：
function [M,N]=julei(tR1)
%函数功能：求出 lamda 截矩阵
tR = tR1;
lamda=unique(tR); %取 A 矩阵不同元素构成的向量，来
确定阈值
L=length(lamda);
lamda = sort(lamda,'descend');
for i = 1:L
tR = tR1;
lamda(i)
tR(find(tR>=lamda(i))) = 1; %令大于 lamda 的为 1
tR(find(tR
2.5.3 对最大最小法构造模糊相似矩阵的传递闭包求出截矩阵，然后进行聚
类，聚类结果如下：
（1）当 1 时，这 8 种产品分为 8 类{x1}，{x2}，{x3}，{x4}，{x5}，{x6}，
{x7}，{x8}。
图七
1 时的截矩阵
（2）当 0.9289
时，这 8 种产品分为 7 类{x1}，{x2}，{x3}，{x4, x5}，{x6}，
{x7}，{x8}。
图八
0.9289
时的截矩阵
（3）当 0.7817
时，这 8 种产品分为 6 类{x1}，{x2, x3}，{x4, x5}，{x6}，
{x7}，{x8}。
图九
0.7817
时的截矩阵
（4）当 0.7739
{x7}。
时，这 8 种产品分为 5 类{x1}，{x2, x3}，{x4, x5, x8}，{x6}，
图十
0.7739
时的截矩阵
（5）当 0.7669
时，这 8 种产品分为 4 类{x1}，{x2, x3}，{x4, x5, x6, x8}，
{x7}。
图十一
0.7669
时的截矩阵
（6）当 0.7541
时，这 8 种产品分为 3 类{x1}，{x2, x3, x7}，{x4, x5, x6, x8}。
图十二
0.7541
时的截矩阵
（7）当 0.7273
时，这 8 种产品分为 2 类{x1}，{x2, x3, x7, x4, x5, x6, x8}。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
