logo资料库

自动控制原理与设计[李中华译]课后答案.pdf

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：9.80M 资料格式：pdf 举报 版权申诉
第1页 / 共672页
第2页 / 共672页
第3页 / 共672页
第4页 / 共672页
第5页 / 共672页
第6页 / 共672页
第7页 / 共672页
第8页 / 共672页
资料共672页，剩余部分请下载后查看
    ch2soln.pdf
    ch3soln.pdf
    ch4soln.pdf
    ch5soln.pdf
    ch6soln.pdf
    ch7soln.pdf
    ch8soln.pdf
    ch9soln.pdf
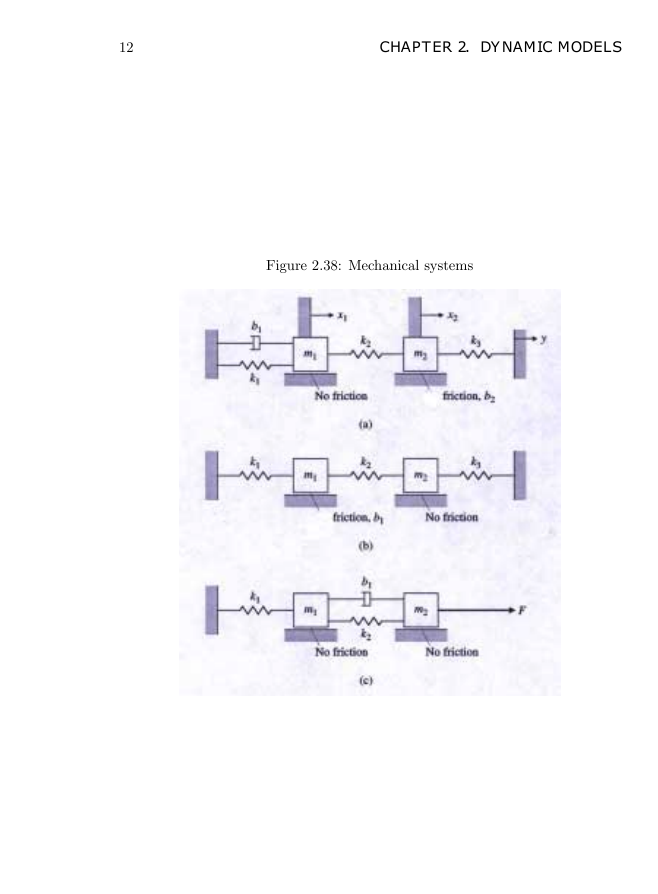
    Chapter 2 Dynamic Models Problems and Solutions for Section 2.1 1. Write the differential equations for the mechanical systems shown in Fig. 2.38. Solution: The key is to draw the Free Body Diagram (FBD) in order to keep the signs right. For (a), to identify the direction of the spring forces on the object, let x2 = 0 and xed and increase x1 from 0. Then the k1 spring will be stretched producing its spring force to the left and the k2 spring will be compressed producing its spring force to the left also. You can use the same technique on the damper forces and the other mass. (a) m1 ¤x1 = −k1x1 − b1 œx1 − k2 (x1 − x2) m2 ¤x2 = −k2 (x2 − x1) − k3 (x2 − y) − b2 œx2
    12 CHAPTER 2. DYNAMIC MODELS Figure 2.38: Mechanical systems
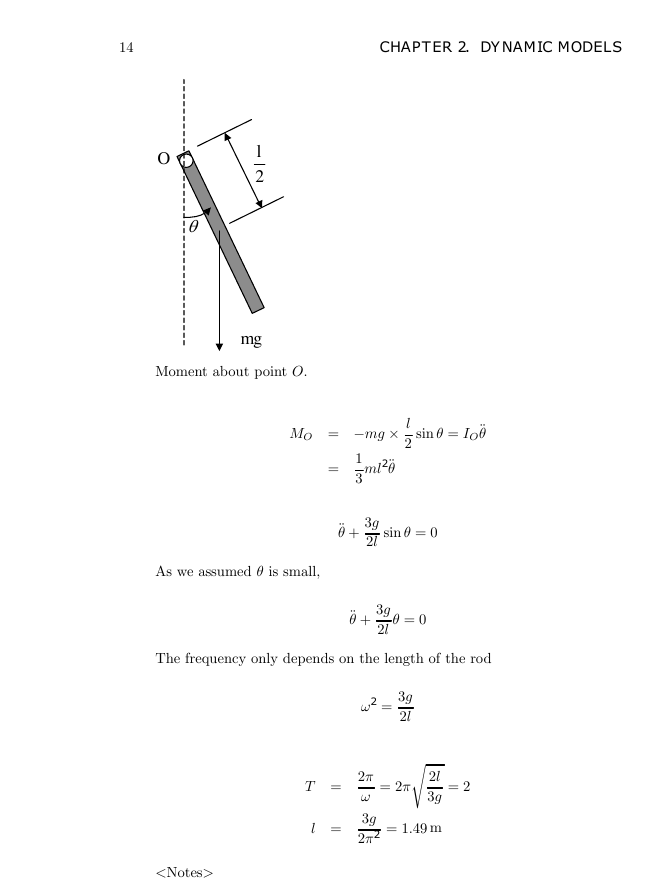
    13 m1 ¤x1 = −k1x1 − k2(x1 − x2) − b1 œx1 m2 ¤x2 = −k2(x2 − x1) − k3x2 m1 ¤x1 = −k1x1 − k2(x1 − x2) − b1( œx1 − œx2) m2 ¤x2 = F − k2(x2 − x1) − b1( œx2 − œx1) 2. Write the equations of motion of a pendulum consisting of a thin, 2-kg stick of length l suspended from a pivot. How long should the rod be in order for the period to be exactly 2 secs? (The inertia I of a thin stick about an endpoint is 1 3 ml2. Assume θ is small enough that sin θ ∼= θ.) Solution: Lets use Eq. (2.14) M = Iα,
    14 CHAPTER 2. DYNAMIC MODELS O G l 2 mg Moment about point O. l 2 sin θ = IO¤θ MO = −mg ml2¤θ = 1 3 As we assumed θ is small, ¤θ + 3g 2l sin θ = 0 ¤θ + 3g 2l θ = 0 The frequency only depends on the length of the rod ω2 = 3g 2l T = l = = 2πs 2l 3g 2π ω 3g 2π2 = 1.49 m = 2 
    Figure 2.39: Double pendulum 15 3g with the well known formula for the period of a point mass hanging with a string with (a) Compare the formula for the period, T = 2πq 2l length l. T = 2πq l g . (b) Important! In general, Eq. (2.14) is valid only when the reference point for the moment and the moment of inertia is the mass center of the body. However, we also can use the formular with a reference point other than mass center when the point of reference is xed or not accelerating, as was the case here for point O. 3. Write the equations of motion for the double-pendulum system shown in Fig. 2.39. Assume the displacement angles of the pendulums are small enough to ensure that the spring is always horizontal. The pendulum rods are taken to be massless, of length l, and the springs are attached 3/4 of the way down. Solution:
    16 CHAPTER 2. DYNAMIC MODELS 1G 2G 3 4 l k m m 3 4 l sin G 1 3 4 l sin G 2 If we write the moment equilibrium about the pivot point of the left pen- dulem from the free body diagram, M = −mgl sin θ1 − k 3 4 l (sin θ1 − sin θ2) cos θ1 3 4 l = ml2¤θ1 ml2¤θ1 + mgl sin θ1 + 9 16 kl2 cos θ1 (sin θ1 − sin θ2) = 0 Similary we can write the equation of motion for the right pendulem −mgl sin θ2 + k 3 4 l (sin θ1 − sin θ2) cos θ2 3 4 l = ml2¤θ2 As we assumed the angles are small, we can approximate using sin θ1 ≈ θ1, sin θ2 ≈ θ2, cos θ1 ≈ 1, and cos θ2 ≈ 1. Finally the linearized equations of motion becomes, ml¤θ1 + mgθ1 + ml¤θ2 + mgθ2 + 9 16 9 16 kl (θ1 − θ2) = 0 kl (θ2 − θ1) = 0 Or
    17 ¤θ1 + ¤θ2 + g l g l θ1 + θ2 + 9 16 9 16 k m k m (θ1 − θ2) = 0 (θ2 − θ1) = 0 4. Write the equations of motion for a body of mass M suspended from a xed point by a spring with a constant k. Carefully dene where the bodys displacement is zero. Solution: Some care needs to be taken when the spring is suspended vertically in the presence of the gravity. We dene x = 0 to be when the spring is unstretched with no mass attached as in (a). The static situation in (b) results from a balance between the gravity force and the spring. From the free body diagram in (b), the dynamic equation results We can manipulate the equation m¤x = −kx − mg. m¤x = −k‡x + m k g· , so if we replace x using y = x + m k g, m¤y = −ky m¤y + ky = 0
    18 CHAPTER 2. DYNAMIC MODELS The equilibrium value of x including the effect of gravity is at x = − m k g and y represents the motion of the mass about that equilibrium point. An alternate solution method, which is applicable for any problem involving vertical spring motion, is to dene the motion to be with respect to the static equilibrium point of the springs including the effect of gravity, and then to proceed as if no gravity was present. In this problem, we would dene y to be the motion with respect to the equilibrium point, then the FBD in (c) would result directly in 5. For the car suspension discussed in Example 2.2, m¤y = −ky. (a) write the equations of motion (Eqs. (2.10) and (2.11)) in state-variable form. Use the state vector x = [ x œx y œy ]T . (b) Plot the position of the car and the wheel after the car hits a unit bump (i.e., r is a unit step) using MATLAB. Assume that m1 = 10 kg, m2 = 350 kg, kw = 500, 000 N/m, ks = 10, 000 N/m. Find the value of b that you would prefer if you were a passenger in the car. Solution: (a) We can arrange the equations of motion to be used in the state- variable form ¤x = − ks m1 x − = − ks m1 ¤y = x + ks m2 b m1 kw œx + ks m1 y + b m1 + m1¶ x − b m1 b m2 œx − ks m2 y − œx + b m2 œy œy − ks m1 kw m1 x + kw m1 r y + b m1 œy + kw m1 r So, for the given sate vector of x = [ x form will be, œx y œy ]T , the state-space œx ¤x œy ¤y   = −‡ ks m1 m1· − b 0 + kw 0 ks m2 1 0 0 ks b m1 m1 m1 0 0 1 m2 − ks m2 − b b m2   x œx y œy + 0 kw m1 0 0  r (b) Note that b is not the damping ratio, but damping. We need to nd the proper order of magnitude for b, which can be done by trial and
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料