2023年湖北鄂州中考数学真题及答案.doc-资料库

第1页 / 共32页

第2页 / 共32页

第3页 / 共32页

第4页 / 共32页

第5页 / 共32页

第6页 / 共32页

第7页 / 共32页

第8页 / 共32页

2023 年湖北鄂州中考数学真题及答案注意事项： 1．本试卷共 8 页，满分 120 分，考试时间 120 分钟． 2．答题前考生务必将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置． 3．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．答在试卷上无效． 4．非选择题用 0.5 毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内．答在试卷上无效． 5．考生必须保持答题卡的整洁．考试结束后，请将本试卷和答题卡一并上交．一、选择题（本大题共 10 小题，每小题 3 分，共计 30 分） ·祝考试顺利· 1．10 的相反数是（） A．－10 B．10 2．下列运算正确的是（） C．  1 10 D． 1 10 A． 2 a  3 a  5 a B． 2 a a  3  5 a C． 2 a  3 a  5 a D． 32 a 5 a 3．中华鲟是地球上最古老的脊椎动物之一，距今约有 140000000 年的历史，是国家一级保护动物和长江珍稀特有鱼类保护的旗舰型物种，3 月 28 日是中华鲟保护日，有关部门进行放流活动，实现鱼类物种的延续并对野生资源形成持续补充．将 140000000 用科学记数法表示应为（） A． 14 10 7 B． 1.4 10 8 C． 0.14 10 9 D． 9 1.4 10 4．下列立体图形中，主视图是圆的是（） A． B． C． D． 5．如图，直线 AB CD ，GE EF 于点 E．若 BGE  60  ，则 EFD 的度数是（） A．60 B．30 C． 40 D． 70

6．已知不等式组 x a       1 x  2 b 的解集是 1    ，则 1x a b 2023  （） A．0 B． 1 C．1 D．2023 7．象棋起源于中国，中国象棋文化历史悠久．如图所示是某次对弈的残图，如果建立平面直角坐标系，使棋子“帅”位于点  2, 1   的位置，则在同一坐标系下，经过棋子 “帅”和“马”所在的点的一次函数解析式为（） A． y x  1 B． y x  1 C． 2 x y  1 D． 2 x y  1 8．如图，在 ABC 中， ABC  90  ， ACB  30  ， AB  ，点O 为 BC 的中点，以O 4 为圆心，OB 长为半径作半圆，交 AC 于点 D ，则图中阴影部分的面积是（） A． 5 3  3 3 B．5 3 4 C．5 3 2 D．10 3 2 9．如图，已知抛物线 y  2 ax   bx c a   的对称轴是直线 1x  ，且过点 0  1,0 ，顶点在第一象限，其部分图象如图所示，给出以下结论：① ab  ；② 4 0 a  2 b c   ； 0 ③3 a c  ；④若  A x y ，  0  , 1 1 x B x y （其中 1 , 2 2 x ）是抛物线上的两点，且 1 x 2 x 2  ， 2  y 则 1 y ，其中正确的选项是（ 2 ） A．①②③ B．①③④ C．②③④ D．①②④ 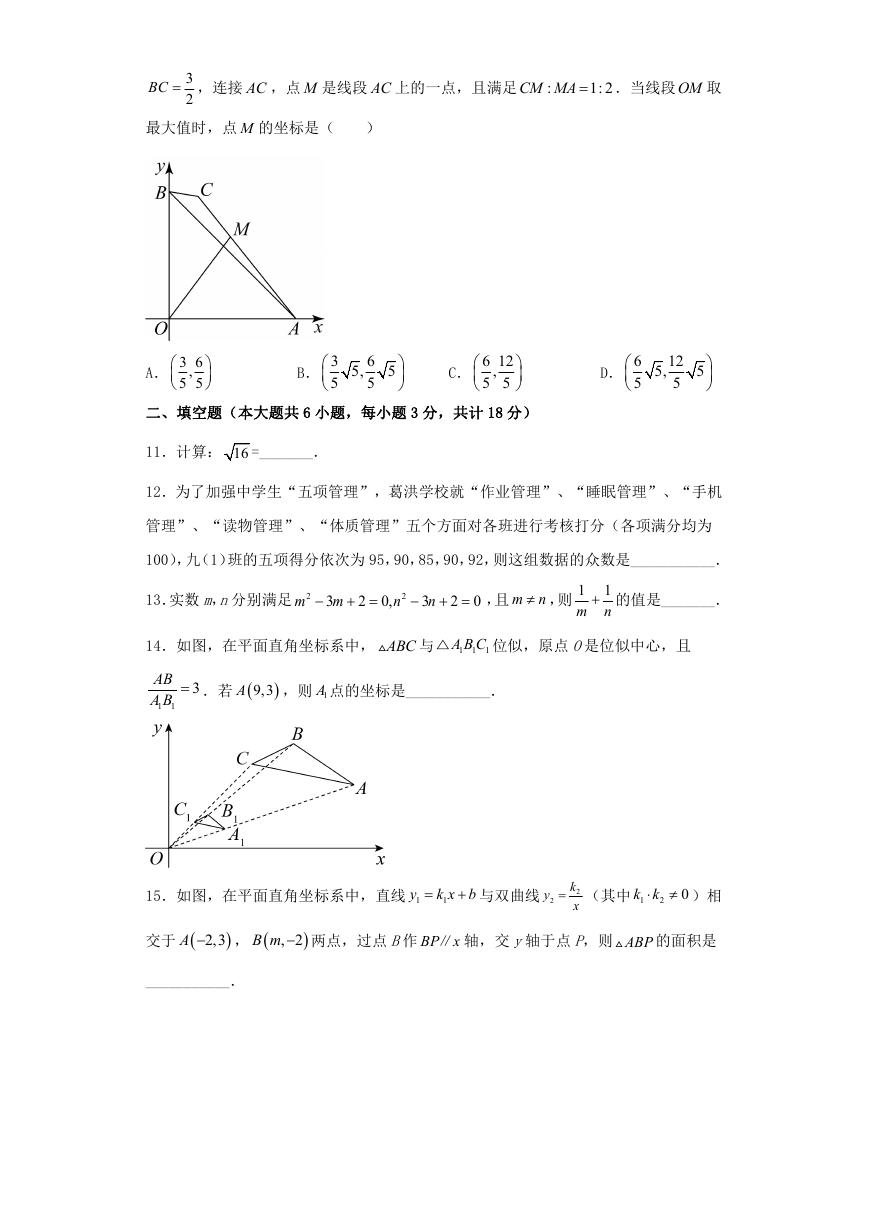10．如图，在平面直角坐标系中，O 为原点， OA OB  3 5 ，点C 为平面内一动点，

BC  ，连接 AC ，点 M 是线段 AC 上的一点，且满足 : CM MA  ．当线段OM 取 1: 2 3 2 最大值时，点 M 的坐标是（） A．    3 6, 5 5    B．    3 5 65, 5 5    C．    6 12, 5 5    D．    6 5 125, 5 5    二、填空题（本大题共 6 小题，每小题 3 分，共计 18 分） 11．计算： 16 =_______． 12．为了加强中学生“五项管理”，葛洪学校就“作业管理”、“睡眠管理”、“手机管理”、“读物管理”、“体质管理”五个方面对各班进行考核打分（各项满分均为 100），九（1）班的五项得分依次为 95，90，85，90，92，则这组数据的众数是___________． 13．实数 m，n分别满足 2 m  3 m   2 2 0, n  3 n   2 0 ，且 m n ，则 1 1 m n  的值是_______． 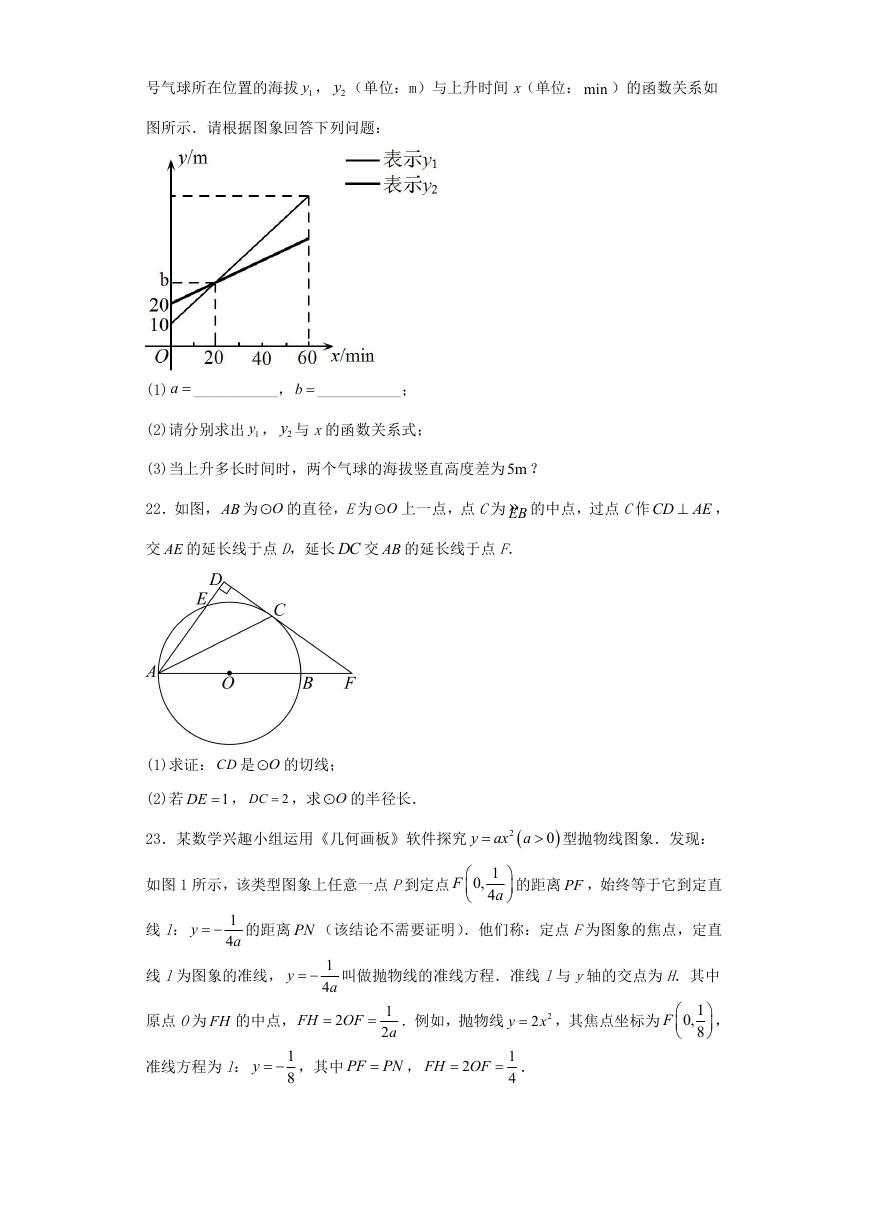14．如图，在平面直角坐标系中， ABC A B C△ 与 1 1 1 位似，原点 O是位似中心，且 AB A B 1 1  ．若  3 A 9,3 ，则 1A 点的坐标是___________． y 15．如图，在平面直角坐标系中，直线 1  k x b 1  与双曲线 y 2  （其中 1 k k k 2 x  ）相 0 2 交于  A  ，  2,3  B m  两点，过点 B作 BP x∥ 轴，交 y轴于点 P，则 ABP , 2  的面积是 ___________．

16．2002 年的国际数学家大会在中国北京举行，这是 21 世纪全世界数学家的第一次大聚会．这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图，世人称之为“赵爽弦图”．如图，用四个全等的直角三角形（ Rt AHB Rt BEC Rt CFD Rt DGA △ ≌ △ ≌ △ ≌ △ ）拼成“赵爽弦图”，得到正方形 ABCD 与正方形 EFGH ，连接 AC 和 EG ， AC 与 DF 、 EG 、 BH 分别相交于点 P、O、Q，若 BE EQ  ，则 3: 2 : OP OE 的值是___________．三、解答题（本大题共 8 小题，17~21 题每题 8 分，22~23 每题 10 分，24 题 12 分，共计 72 分） a 17．先化简，再求值： 2 a  1  1 2  a 1 ，其中 2 a  ． 18．如图，点 E是矩形 ABCD 的边 BC 上的一点，且 AE AD ． (1)尺规作图（请用 2B 铅笔）：作 DAE 的平分线 AF ，交 BC 的延长线于点 F，连接 DF ．（保留作图痕迹，不写作法）； (2)试判断四边形 AEFD 的形状，并说明理由． 19．为庆祝建党 100 周年，让同学们进一步了解中国科技的快速发展，东营市某中学九（1）班团支部组织了一次手抄报比赛．该班每位同学从 A．“北斗卫星”；B．“5G 时代”；C．“东风快递”；D．“智轨快运”四个主题中任选一个自己喜欢的主题．统计同学们所选主题的频数，绘制成以下不完整的统计图，请根据统计图中的信息解答下列

问题：（1）九（1）班共有________名学生；（2）补全折线统计图；（3）D所对应扇形圆心角的大小为________；（4）小明和小丽从 A、B、C、D四个主题中任选一个主题，请用列表或画树状图的方法求出他们选择相同主题的概率． 20．鄂州市莲花山是国家 4A 级风景区，元明塔造型独特，是莲花山风景区的核心景点，深受全国各地旅游爱好者的青睐．今年端午节，景区将举行大型包粽子等节日庆祝活动．如图 2，景区工作人员小明准备从元明塔的点 G处挂一条大型竖直条幅到点 E处，挂好后，小明进行实地测量，从元明塔底部 F点沿水平方向步行 30 米到达自动扶梯底端 A点，在 A点用仪器测得条幅下端 E的仰角为30 ；接着他沿自动扶梯 AD 到达扶梯顶端 D点，测得点 A和点 D的水平距离为 15 米，且 tan DAB  ；然后他从 D点又沿 4 3 水平方向行走了 45 米到达 C点，在 C点测得条幅上端 G的仰角为 45 ．（图上各点均在同一个平面内，且 G，C，B共线，F，A，B共线，G、E、F共线，CD AB∥ ，GF FB ）． (1)求自动扶梯 AD 的长度； (2)求大型条幅 GE 的长度．（结果保留根号） 21．1 号探测气球从海拔10m 处出发，以1m/min 的速度竖直上升．与此同时，2 号探测气球从海拔 20m 处出发，以 m/min a 的速度竖直上升．两个气球都上升了1h ．1 号、2

号气球所在位置的海拔 1y ， 2y （单位：m）与上升时间 x（单位： min ）的函数关系如图所示．请根据图象回答下列问题： (1) a ___________，b  ___________； (2)请分别求出 1y ， 2y 与 x的函数关系式； (3)当上升多长时间时，两个气球的海拔竖直高度差为5m ？ 22．如图，AB 为 O 的直径，E为 O 上一点，点 C为 »EB 的中点，过点 C作CD AE ，交 AE 的延长线于点 D，延长 DC 交 AB 的延长线于点 F． (1)求证： CD 是 O 的切线； (2)若 DE  ， 1 DC  ，求 O 的半径长． 2 23．某数学兴趣小组运用《几何画板》软件探究如图 1 所示，该类型图象上任意一点 P到定点 F 2  ax a  型抛物线图象．发现： 0   y 10, 4 a       的距离 PF ，始终等于它到定直线 l： y   的距离 PN （该结论不需要证明）．他们称：定点 F为图象的焦点，定直 1 4 a 线 l为图象的准线， y   叫做抛物线的准线方程．准线 l与 y轴的交点为 H．其中 1 4 a 原点 O为 FH 的中点， FH  2 OF  ．例如，抛物线 1 2 a y x ，其焦点坐标为 22 F    10, 8    ，准线方程为 l： y   ，其中 PF PN ， 1 8 FH  2 OF  ． 1 4

【基础训练】 (1)请分别直接写出抛物线 y x 2 1 4 的焦点坐标和准线 l的方程：___________， ___________；【技能训练】 (2)如图 2，已知抛物线 y x 2 1 4 上一点  , P x y 0 0  x  到焦点 F的距离是它到 x轴距 0 0  离的 3 倍，求点 P的坐标；【能力提升】 (3)如图 3，已知抛物线 y x 2 1 4 的焦点为 F，准线方程为 l．直线 m： y 1 x 2  交 y轴 3 于点 C，抛物线上动点 P到 x轴的距离为 1d ，到直线 m的距离为 2d ，请直接写出 1 d d 2 的最小值；【拓展延伸】该兴趣小组继续探究还发现：若将抛物线 y  2  ax a  平移至 0  y   a x h   2   k a  ．抛 0  物线 y   a x h   2   k a  内有一定点 0  , F h k     1 4 a    ，直线 l过点 , M h k     1 4 a    且与 x轴平行．当动点 P在该抛物线上运动时，点 P到直线 l的距离 1PP 始终等于点 P到点 F的距离（该结论不需要证明）．例如：抛物线 y  2  x  2 1  上的动点 P到点 3 F    251, 8    的距离等于点 P到直线 l： y  的距离． 23 8 请阅读上面的材料，探究下题： (4)如图 4，点 D    31, 2    是第二象限内一定点，点 P是抛物线 y 21 x 4 1  上一动点，当 PO PD 取最小值时，请求出 POD 的面积． 24．如图 1，在平面直角坐标系中，直线 l y 轴，交 y轴的正半轴于点 A ，且 OA  ， 2 点 B是 y轴右侧直线 l上的一动点，连接OB ．

(1)请直接写出点 A的坐标； (2)如图 2，若动点 B满足 ABO  30  ，点 C为 AB 的中点， D 点为线段OB 上一动点，连接CD ．在平面内，将 BCD△ 沿CD 翻折，点 B的对应点为点 P，CP 与OB 相交于点 Q，当CP AB 时，求线段 DQ 的长； (3)如图 3，若动点 B满足 AB OA  ， EF 为 OAB  2 的中位线，将 BEF△ 绕点 B在平面内逆时针旋转，当点 O、E、F三点共线时，求直线 EB与 x轴交点的坐标； (4)如图 4，OC 平分 AOB 交 AB 于点 C ， AD OB 于点 D ，交OC 于点 E ， AF 为 AEC△ 的一条中线．设 ACF△ ， ODE  ， OAC 的周长分别为 1C ， 2C ， 3C ．试探究： c  在 B点的运动过程中，当 1 c 3 2 c 2  时，请直接写出点 B的坐标． 11 8

资料库

2023年湖北鄂州中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料