2 Ξ 第 15 卷 第 2 期 2002 年 6 月 盐城工学院学报 Journal of Yancheng Institute of Technology Vol. 15 No. 2 Jun. 2002 基于小波变换的语音信号去噪 李蕴华 (南通工学院 信息工程系 ,江苏 南通 　226007) 摘 　要 :讨论了离散小波变换在语音去噪中的应用 。根据语音中浊音段和清音段的特点 ,采 用了不同的阈值方案 ,可以保证在失真较小的前提下 ,获得更好的去噪效果 。 关键词 :小波变换 ; 语音去噪 ; 阈值 中图分类号 :TN850. 5 　　　文献标识码 :A 　　　文章编号 :1671 - 5322 (2002) 02 - 0032 - 04 　　语音信号的去噪是语音处理的一个重要课 题 。当噪声与语音的频谱相似时 ,传统的单纯时 域滤波或频域滤波往往无法达到很好的效果 。离 散小波变换是一种时 频分析法 ,在时频两域都能 表征信号的局部特性 。利用小波变换实现信号的 去噪 ,具有较好的效果 。 在本文中 ,笔者将语音信号划分成浊音和清 音两部分 ,根据它们各自的特点 ,在采用小波变换 进行去噪时 ,选择了不同的阈值方案进行了性能 测试 。 1 　离散小波变换理论 有限序列 s ( n) 的离散小波变换 (DWT) 定义 为 : DWT( s , 2 j , k2 j ) = Dj , k = ∑ n ∈Z s ( n) hj 1 ( n - 2 j k) , s ( n) hj 0 ( n - 2 j k) Cj , k = ∑ n ∈Z ( j , k , n ∈Z) 反变换 IDWT 定义为 : s ( n) = ∑ Dj , k gj 1 ( n - 2 j k) + J ∑ n ∈Z j = 1 0 ( n - 2 j k) Cj , k gj ∑ n ∈Z 式中 h0 ( n) 和 g0 ( n) 分别被称为尺度序列 和对偶尺度序列 , h1 ( n) 和 g1 ( n) 分别被称为小 波序列和对偶小波序列。低通滤波器 h0 及带通 滤波器 h1 形成了一对镜像滤波器组 h1 ( n) = ( - 1) 1 - n h0 (1 - n) 。Cj , k 和 Dj , k 分别被称为 2 - j 分 辨率下的离散逼近信号 (低频系数) 和离散细节信 号 (高频系数) 。 Dj , k和 Cj , k 可由 Mallat 塔式算法算出 , 运算过程 为 : 输入 : C0 ,n (输入序列 s ( n) ) , J (分解层次) 运算过程 :for j = 1 to J 　{ Dj , k = ∑ n ∈Z 　Cj , k = ∑ n ∈Z h1 ( n - 2 k) Cj - 1 , n ; h0 ( n - 2 k) Cj - 1 , n ; 　} 输出 : Cj , k , Dj , k 。( Cj , k , Dj , k 分别为第 j 个分解层 次上第 k 个点的逼近信号和细节信号) 。 通过滤波器 h1 和 h0 ,将信号分解成低频空 间 C1 和高频空间 D1 ,然后每次只对低频空间进 一步分解 ,对每层的高频系数不再继续分解。 对于小波的各层高频系数可采用一定的阈值 进行量化处理 ,以去除噪声 。然后根据各层低频 系数及量化后的高频系数 ,实现信号的重构 。 2 　小波去噪中阈值的选择 在对小波系数进行量化时 ,选用何种阈值规 则 ,会影响到最终去噪效果的好坏 。在保证失真 小的前提下 ,尽可能提高信噪比是选择合适阈值 的原则 。阈值方案一般有两种 :硬阈值法及软阈 值法 。前者主要保留信号的低频成分 ,衰减了大 部分高频成分 ,使得主要表现为高频信号的噪声 收稿日期 :2001 - 03 - 18 　作者简介 :李蕴华 (1965 ) ,女 ,江苏南通市人 ,南通工学院讲师 ,硕士 ,研究方向为数字信号处理 。 

第 2 期 李蕴华 :基于小波变换的语音信号去噪 　　　 ·33· 部分能被有效去除 ,但语音中的大量高频部分 (如 清音) 也被去掉 ,产生失真 。故我们采用软阈值处 理 。软阈值方法有 : (1) 采用 Stein 的无偏似然估 计原理 (SURE) 进行阈值选择 。对一个给定的阈 值 t ,得到它的似然估计 ,再将非似然 t 最小化 , 就得到了所选的阈值 ; (2) 用极大极小原理 (Min imaxi) 选择阈值 。它以处理后信号与原始信号的 最大概率逼近为约束条件 ; (3) 启发式阈值选择 。 它是一种最优预测变量阈值选择方法 ; (4) 固定阈 值形式 ,其值为 2lg(length ( s) ) ,其中 length ( s) 为 信号的长度 。在这 4 种方法中 ,前两种阈值选取 规则比较保守 (它只将部分系数置 0) ,当信号的 高频信息有一部分在噪声范围内时 ,采用这两种 阈值 ,可以将弱小信号提取出来 ;后两种阈值在去 除噪声时 ,显得更为有效 ,但有可能把有用的高频 特征当作噪声去除 。 语音信号可以被分成浊音段及清音段两部 分 ,这两部分的主要区别是 : 浊音呈现出准周期 性 ,其周期即为该段的基音周期 ,且含有较多的低 频成分 ,容易和高频噪声区别开 。清音的信号波 形类似于白噪声 ,与浊音相比 ,频率较高且无周期 性 。若语音中掺入了含高频成分的噪声 ,对浊音 段和清音段应采用不同的阈值方案 ,才能获得最 佳的去噪效果 。由前面的分析可知 ,对于清音 ,可 采用 (1) 、(2) 两种阈值规则 ,不至于损失过多的有 用信号 ,而对于浊音 ,可采用 (3) 、(4) 两种阈值规 则 ,更有效地去除噪声 。 3 　浊音段和清音段的划分 由于针对清 、浊音我们采用不同的阈值方案 , 故准确划分清 、浊音段是一个关键性的问题 。逆 滤波法可以有效的判别是否浊音段 ,并可确定基 音周期 。逆滤波法过程见图 1 : 图 1 　清音和浊音的区分 Fig. 1 　Division of unvoiced and voiced speech 　　对于浊音来说 ,由于其具有准周期性 ,归一化 变形自相关函数在基音周期可能存在的 2. 5～15 ms 处会出现尖峰 (峰点值大于 0. 25) ,该尖峰位置 其实就是基音周期判断的依据 。而对于清音来 说 ,则无明显峰起 。用这种方法可以准确的区分 出清浊音 。 在整个过程中 ,分析窗的最小长度的选取 ,应 是两倍的基音周期 ,太小无峰点出现 ,而太大则引 入了不希望有的平滑 。 另外 ,通过实验我们发现 ,利用该方法也能准 确的区分含噪语音的清 、浊音段 。 4 　去噪实验及结果 利用话筒将语音信号采集到计算机 ,并人为 掺入高斯白噪声 ,生成数据文件供实验使用 。 在去噪实验中 ,我们选用了 Biorthogonal 函数 作为小波函数 ,它具有线形相位特性 ,主要用于信 号的重构中 。实验表明 ,采用这种函数能得到较 好的去噪效果 。小波分解层次 J = 6 。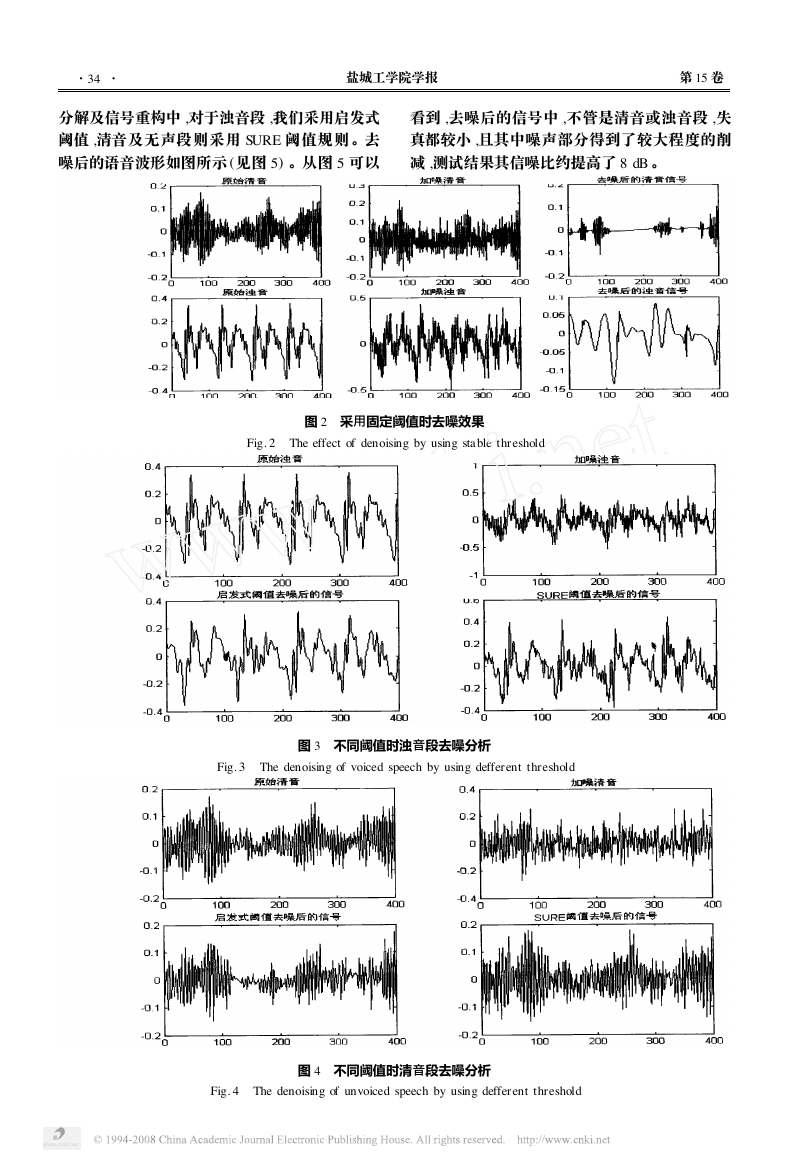 在对高频小波系数量化中 ,对于浊音段及清 音段我们比较了各种不同的软阈值方案 ,发现采 用固定阈值 2lg(length ( s) ) 形式 ,由于去掉了较 多的高频成分 ,引入了平滑 ,无论是对于清音还是 浊音 ,都存在较大失真 (如图 2) ,故在语音去噪中 我们不采用该阈值 。 为得到较好的去噪效果 ,经实验发现 ,对于浊 音段 ,可采用启发式阈值方案 ,而对于清音段 ,则 采用 SURE 阈值方案 。图 3 及图 4 是采取不同的 阈值法下的浊音 、清音的原始波形和去噪后波形 。 从图 3 和图 4 可以看出 ,对于浊音 ,采用启发 式阈值法比采用 SURE 阈值法可获取更强的去噪 效果 ,但是对于频率成分与噪声很相似的清音 ,启 发式阈值法会去掉一些有用的清音 ,产生失真 ,而 应用 SURE 阈值则可保留这部分清音 。由此可 见 ,针对浊 、清音不同特点 ,浊音部分选取启发式 阈值方案 ,清音部分选取 SURE 阈值方案 ,可使整 个语音段能达到最佳去噪效果 。 我们用话筒录下语音“工学院”3 个字 ,采样 频率为 20 kHz ,数据长 30 000 点 。加入白噪声 ,构 成含噪信号 (信噪比 RSN = 1 dB) 。利用逆滤波法 将含噪语音分成浊 、清音段 ,浊音段约有 1 400 点 , 剩余的是清音段及无声段 。在利用小波变换进行 

·43·　　　 盐城工学院学报 第 15 卷 分解及信号重构中 ,对于浊音段 ,我们采用启发式 阈值 ,清音及无声段则采用 SURE 阈值规则 。去 噪后的语音波形如图所示 (见图 5) 。从图 5 可以 看到 ,去噪后的信号中 ,不管是清音或浊音段 ,失 真都较小 ,且其中噪声部分得到了较大程度的削 减 ,测试结果其信噪比约提高了 8 dB 。 图 2 　采用固定阈值时去噪效果 Fig. 2 　The effect of denoising by using stable threshold 图 3 　不同阈值时浊音段去噪分析 Fig. 3 　The denoising of voiced speech by using defferent threshold 图 4 　不同阈值时清音段去噪分析 Fig. 4 　The denoising of unvoiced speech by using defferent threshold 

第 2 期 李蕴华 :基于小波变换的语音信号去噪 　　　 ·53· 图 5 　一段语音信号的去噪分析 Fig. 5 　The denoising analysis of a speech segment 5 　结束语 本文根据语音清音段及浊音段的不同特点 , 参考文献 : 采用了不同的阈值进行小波去噪 ,并获得了较好 的去噪效果 。 1 秦前清. 实用小波分析 M . 西安 :西安电子科技大学出版社 ,1998. 2 拉宾那 L R. 语音信号数字处理 M . 北京 :科学出版社 ,1984. 3 张贤达. 现代信号处理 M . 北京 :清华大学出版社 ,1998. 4 李世雄. 小波变换及其应用 M . 北京 :高等教育出版社 ,1997. Speech Signal Denoising based on Wavelet Transform (Department of information Engineering of Nantong Institute of Technology ,Jiangsu Nantong　226007 ,China) LI Yun hua Abstract : In this paper , an application of wavelet transform for speech signal denoising is discussed. According to the properties of voiced segment and unvoiced segment in speech signal , we use different thresholds. And a better effect of denoising is derived with less distortion. Keywords :wavelet transform ; speech signal denoising ; threshold