logo资料库

基于MATLAB的状态反馈的极点配置.doc

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.14M 资料格式：doc 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    《现代控制理论》状态反馈的极点配 置 课 程 名 称 现代控制理论 所 在 学 院 控制工程学院 专 业 工业自动化 082 班 指 导 教 师 实 验 人 员 学 号 1 / 7
    2011 年 12 月 课程实验报告 状态反馈控制系统的设计与实现 6111 实验日期 2011.12 朱明 实验小组 教师 评阅 A B C /D 实验 名称 实验 地点 指导 老师 一、实验目的 1、掌握极点配置定理及状态反馈控制系统的设计方法 2、比较输出反馈与状态反馈的优缺点 3、训练 Matlab 程序设计能力 二、实验内容 1、实验原理 1.1 首先设计一个二阶系统为： G )s( 1 1s2  2 s  1.2设计要配置的极点为： S1=-2; S2=-3; 1.3 状态反馈任意配置闭环极点的充分必要条件是被控系可控。输出至状态 微分的反馈任意配置闭环极点的充分必要条件是被控系统可观测。 因此首先根据系统可控性判别阵： = 2 / 7
    同样，根据可观性判别阵： = 1.4 状态微分反馈控制器与输出至状态微分反馈的设计方法： 首先状态反馈系统的动态方程为： = - ) , 系统原来的 矩阵现在变为 - 。又因为系统的特征多项式只与 矩阵 有关，所以可让求得期望配置极点的特征多项式与状态反馈后的系统的特 征多项式( 阵 的值了。 本实验中： )对应阶次的系数相等，这样就可求出状态反馈 K1=5; k2=3; 同样输出至状态微分反馈系统的动态方程为 = - ) + , 系统原来的 矩阵现在变为 - 。又因为系统的特征多项式只与 矩阵 有关，所以可让求得期望配置极点的特征多项式与输出至状态微分反馈后 的系统的特征多项式( )对应阶次的系数相等，这样就可 求出输出至状态微分反馈阵 的值了。 本实验中： H1=3; H2=-1; 2、实验步骤 （1）、打开 matlab 软件，熟悉软件的工作界面。 （2）、创建工程，m 文件。 3 / 7
    （3）、在 m 文件中编写程序，并运行判断系统是否可控，可观及求出 。 （4）、创建 model 文件，用 Simulink 画状态变量图，用阶跃信号输入，观看 三种状态变量图的响应曲线。 （5）、 根据响应曲线分析结果，比较输出至状态微分反馈与状态反馈的优缺 点。总结此次实验。 三、实验设备（设备名称、数量等）： 设备名称 数量 PC 机 Matlab 软件 1 1 备注 主频 2.8Ghz 2.79GHZ 内存 512M windows XP Matlab 6.5 四、实验结果及数据分析 1 程序源代码 可观子程序： function y=keguan(A,C) S=obsv(A,C); r=rank(S); l=length(A); if r == l str = '系统可观' else str = '系统不可观' end 可控子程序： function y=kekong(A,B); S=ctrb(A,B); r=rank(S); l=length(A); if r == l str = '系统可控' 4 / 7
    else str = '系统不可控' end clear 期望配置极点为：S1=-5；S2=-1； 求状态反馈阵 的值及输出反馈阵 的值程序： clc A=[0 1;-1 -1]; b=[0;1]; c=[1 0]; kekong(A,b) keguan(A,c) p=[complex(-2,sqrt(3)) complex(-3,-sqrt(3))] K=acker(A,b,p) H=(acker(A',c',p))' 2 在 model 文件画状态变量图并用 Simulink 进行仿真： 2.1 阶 跃 信 号 作 用 下 没 加 任 何 反 馈 前 系 统 的 状 态 变 量 图 ： 此时响应曲线图为： 2.2 阶跃信号作用下用状态反馈的系统的状态变量图： 此时响应曲线图为： 5 / 7
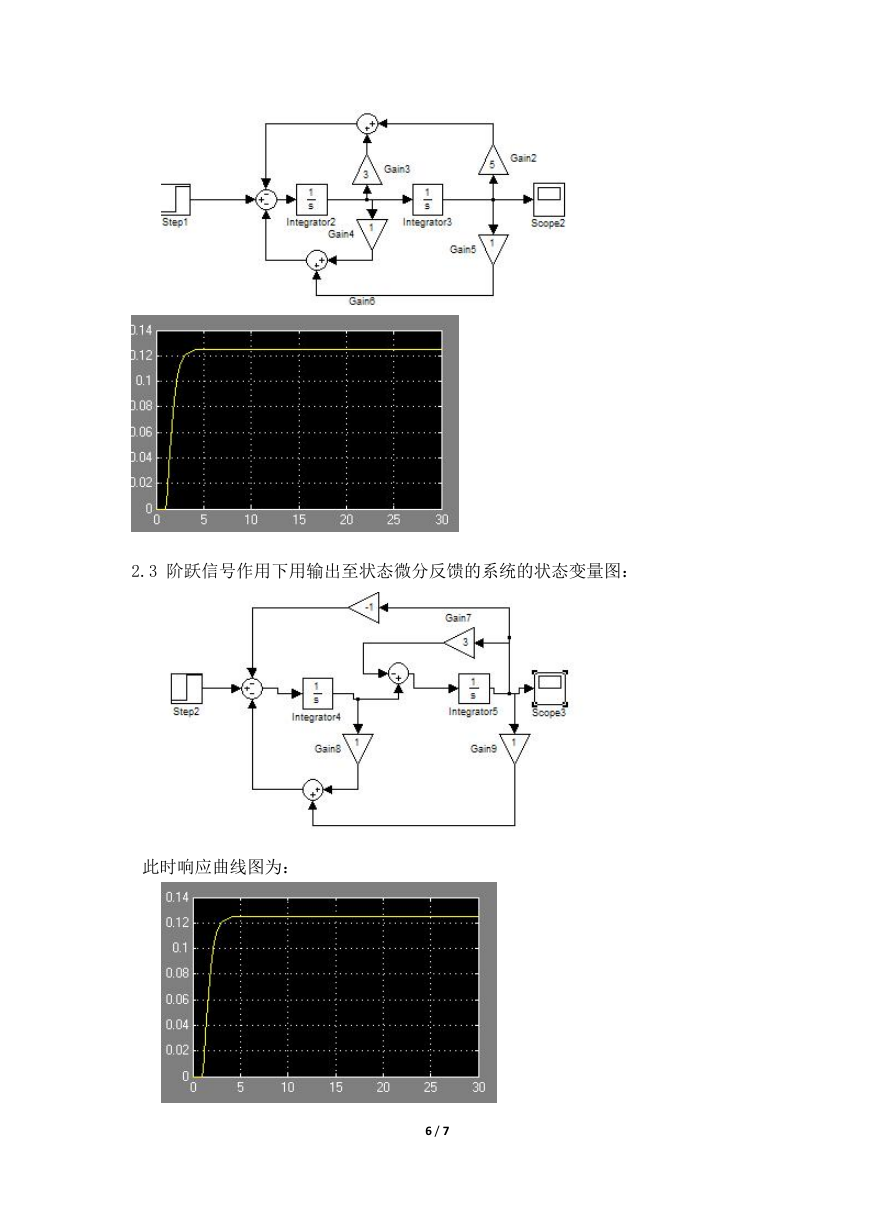
    2.3 阶跃信号作用下用输出至状态微分反馈的系统的状态变量图： 此时响应曲线图为： 6 / 7
    3 实验结果分析： 由上述实验结果： 1、 阶跃信号作用下，没加任何反馈前系统与有反馈系统的响应相比； 增加反馈后系统响应快速性等指标明显变好。 2、 阶跃信号作用下，状态反馈系统与输出至状态微分反馈系统的响 应相比；状态反馈系统的响应各性能指标更佳。 由上述实验结果分析： 1、 没加任何反馈前系统与有反馈系统的响应相比，由于后者能将误差 信息及时返回用于校正系统，从而使系统性能显著提高。 2、 状态反馈系统与输出至状态微分反馈系统的响应相比，由于前者能 反馈更多的校正信息，从而使得系统性能得到优化。 7 / 7
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料