第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
五种常用小波基于MATLAB实现.doc
1.给出五种常用小波基的时域和频域波形图。
与标准的傅里叶变换相比，小波分析中使用到的小波函数具有不唯一性，即
小波函数 (t) 具有多样性。小波分析在工程应用中，一个十分重要的问题就是
最优小波基的选择问题，因为用不同的小波基分析同一个问题会产生不同的结
果。目前我们主要是通过用小波分析方法处理信号的结果与理论结果的误差来判
定小波基的好坏，由此决定小波基。常用小波基有 Haar 小波、Daubechies(dbN)
小波、Mexican Hat(mexh)小波、Morlet 小波、Meyer 小波等 5 种。
（1）Haar 小波
Haar 函数是小波分析中最早用到的一个具有紧支撑的正交小波函数，也是
最简答的一个小波函数，它是支撑域在 [0,1]
t
范围内的单个矩形波。 Haar
函数的定义如下：
(t)
1
1-
0
1
2
1
t
0
t
1
2
其他
Haar 小波在时域上是不连续的，所以作为基本小波性能不是特别好。但它
也有自己的优点，如：
计算简单；
t)2( j
(t) 不但与
2 j
因此，在
[j 正交，而且与自己的整数位移正交。
z]
a 的多分辨率系统中 Haar 小波构成一组最简单的正交归一的小波
族。
( )t 的傅里叶变换是：
4=
（ ）j
2
sin (
a
)
je
/2
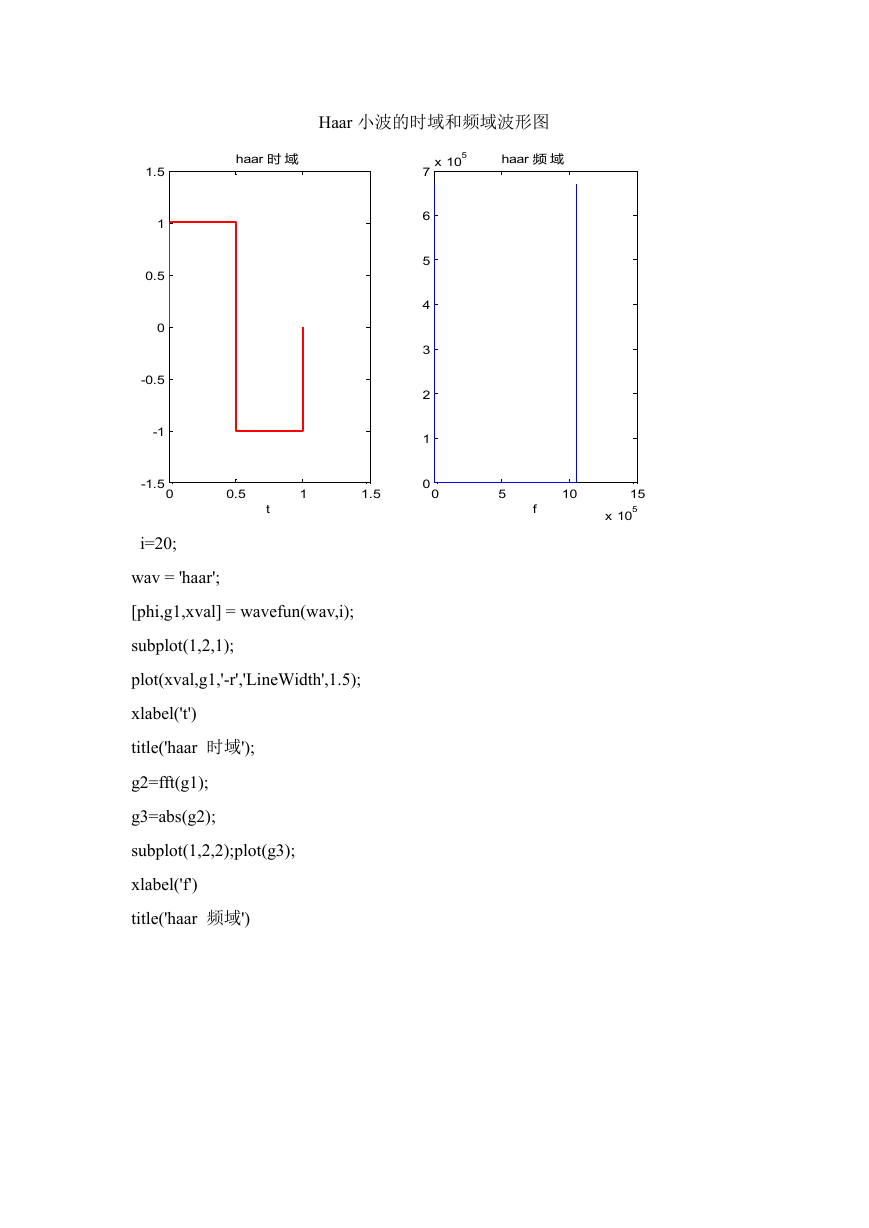
haar 时 域
Haar 小波的时域和频域波形图
x 105
haar 频 域
7
6
5
4
3
2
1
1.5
1
0.5
0
-0.5
-1
-1.5
0
0.5
t
1
1.5
0
0
5
f
10
15
x 105
i=20;
wav = 'haar';
[phi,g1,xval] = wavefun(wav,i);
subplot(1,2,1);
plot(xval,g1,'-r','LineWidth',1.5);
xlabel('t')
title('haar 时域');
g2=fft(g1);
g3=abs(g2);
subplot(1,2,2);plot(g3);
xlabel('f')
title('haar 频域')
（2）Daubechies(dbN)小波
Daubechies 小波是世界著名的小波分析学者 Inrid Daubechies 构造的小波
函数，简写为 dbN，N 是小波的阶数。小波 (t) 和尺度函数 (t) 中的支撑区为
N ， (t) 的消失矩为 N。除
2
外，dbN 不具有对称性（即非线性相位）。
1N
1
dbN 没有明确的表达式（除
1N
外），但转换函数 h 的平方模是明确的。
Daubechies 小波系是由法国学者 Daubechies 提出的一系列二进制小波的总
称，在 Matlab 中记为 dbN，N 为小波的序号，N 值取 2，3，…，10。该小波没
有明确的解析表达式，小波函数φ与尺度函数Φ的有效支撑长度为 2N-1.当 N 取 1
时便成为 Haar 小波。
p
(y)
令
N
1
C
k
0
k
N
1-
k y
k
，其中C k
1-
N
k
为二项式的系数，则有
2
(
)
m
0
2
(cos
2
)p(sin
2
)
2
式中，
(m
0
)
1
2
1
2
N
k
0
-
eh
k
jk
。
Daubechies 小波具有以下特点：
（1）在时域是有限支撑的，即 (t) 长度有限。
( 在=0 处有 N 阶零点。
(t)
（2）在频域
)
（3） (t) 和它的整数位移正交归一，即
（4）小波函数 (t) 可以由所谓“尺度函数” (t) 求出来。尺度函数 (t) 为
低通函数，长度有限，支撑域在 t=0~(2N-1)范围内。
。
k
-(t
k)dt
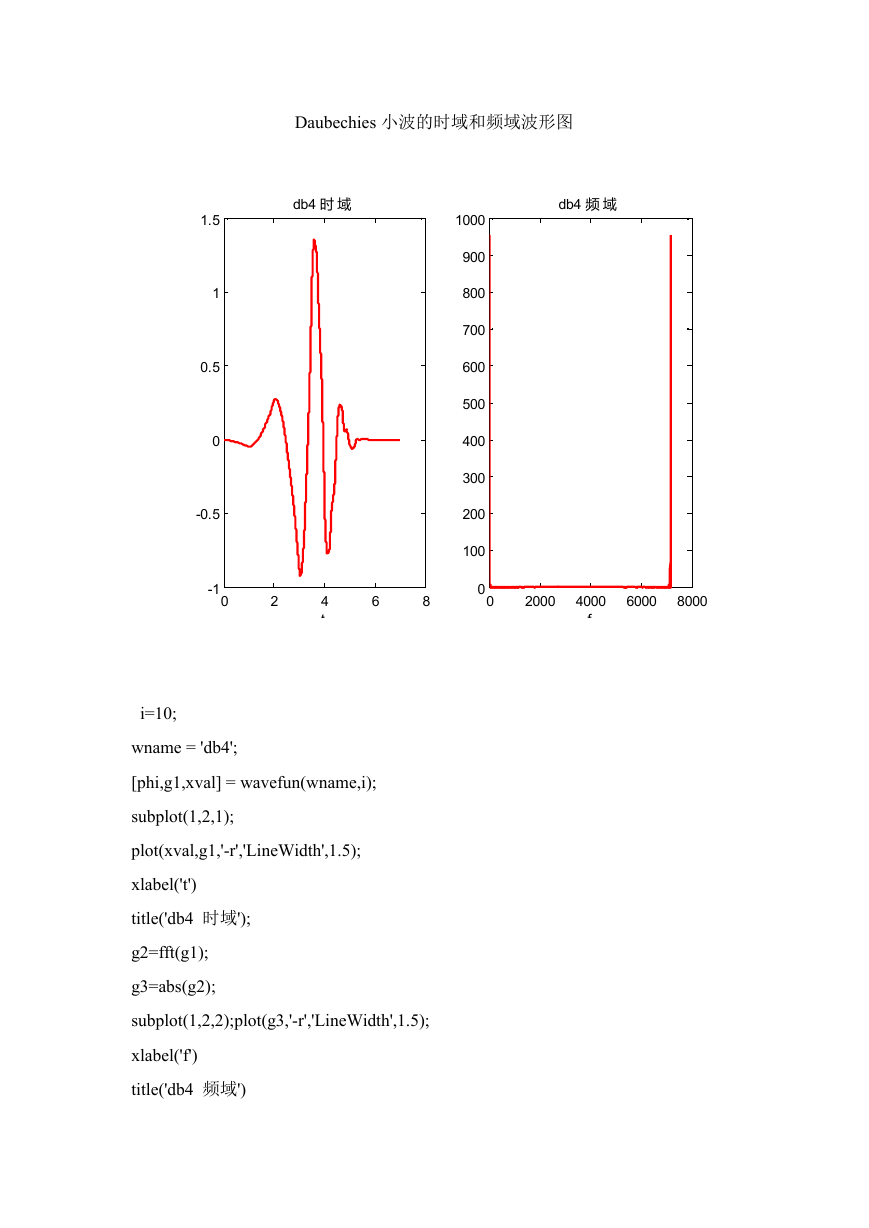
Daubechies 小波的时域和频域波形图
db4 频 域
db4 时 域
1.5
1
0.5
0
-0.5
1000
900
800
700
600
500
400
300
200
100
-1
0
2
4
t
6
8
0
0
2000
4000
f
6000
8000
i=10;
wname = 'db4';
[phi,g1,xval] = wavefun(wname,i);
subplot(1,2,1);
plot(xval,g1,'-r','LineWidth',1.5);
xlabel('t')
title('db4 时域');
g2=fft(g1);
g3=abs(g2);
subplot(1,2,2);plot(g3,'-r','LineWidth',1.5);
xlabel('f')
title('db4 频域')
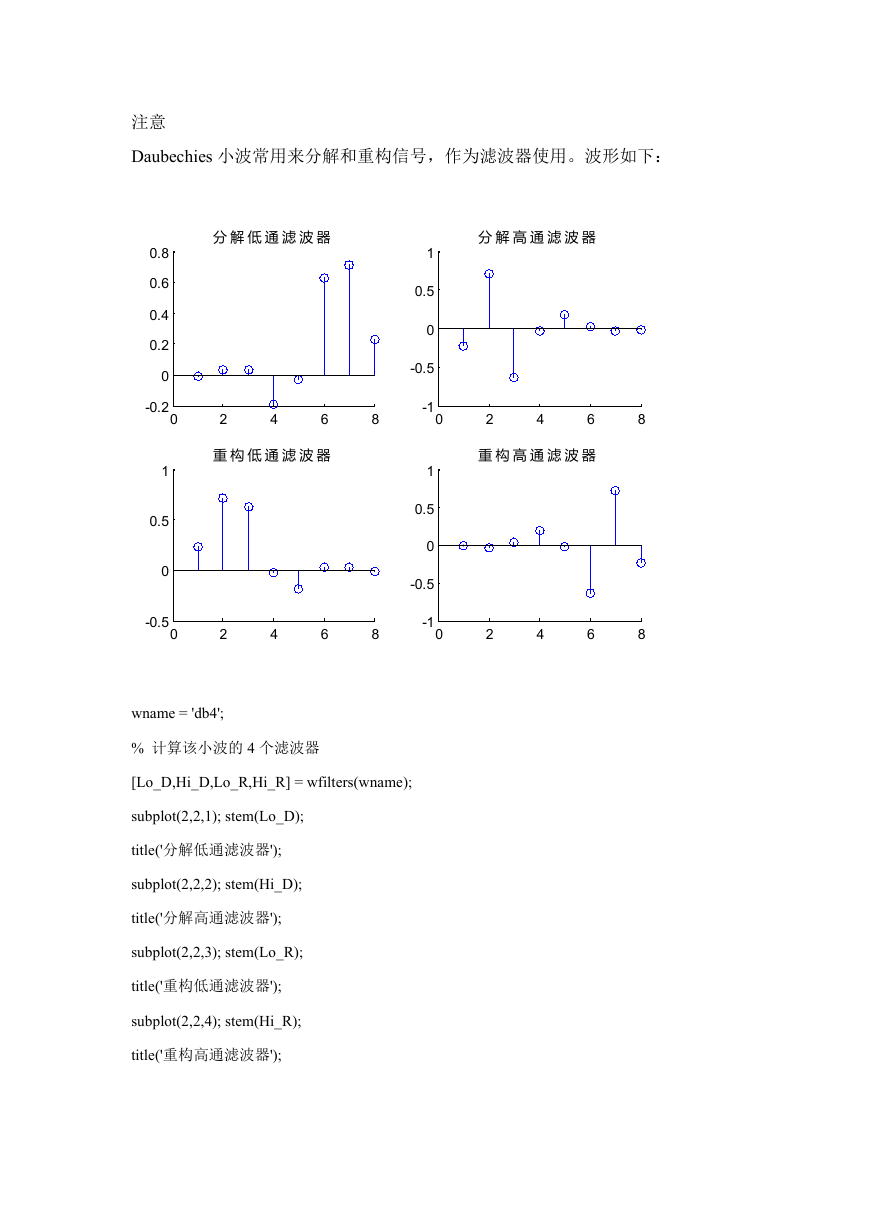
注意
Daubechies 小波常用来分解和重构信号，作为滤波器使用。波形如下：
分 解 高 通 滤 波 器
2
4
6
8
重 构 高 通 滤 波 器
2
4
6
8
0.8
0.6
0.4
0.2
0
-0.2
0
1
0.5
0
-0.5
0
分 解 低 通 滤 波 器
2
4
6
8
重 构 低 通 滤 波 器
2
4
6
8
1
0.5
0
-0.5
-1
0
1
0.5
0
-0.5
-1
0
wname = 'db4';
% 计算该小波的 4 个滤波器
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(wname);
subplot(2,2,1); stem(Lo_D);
title('分解低通滤波器');
subplot(2,2,2); stem(Hi_D);
title('分解高通滤波器');
subplot(2,2,3); stem(Lo_R);
title('重构低通滤波器');
subplot(2,2,4); stem(Hi_R);
title('重构高通滤波器');
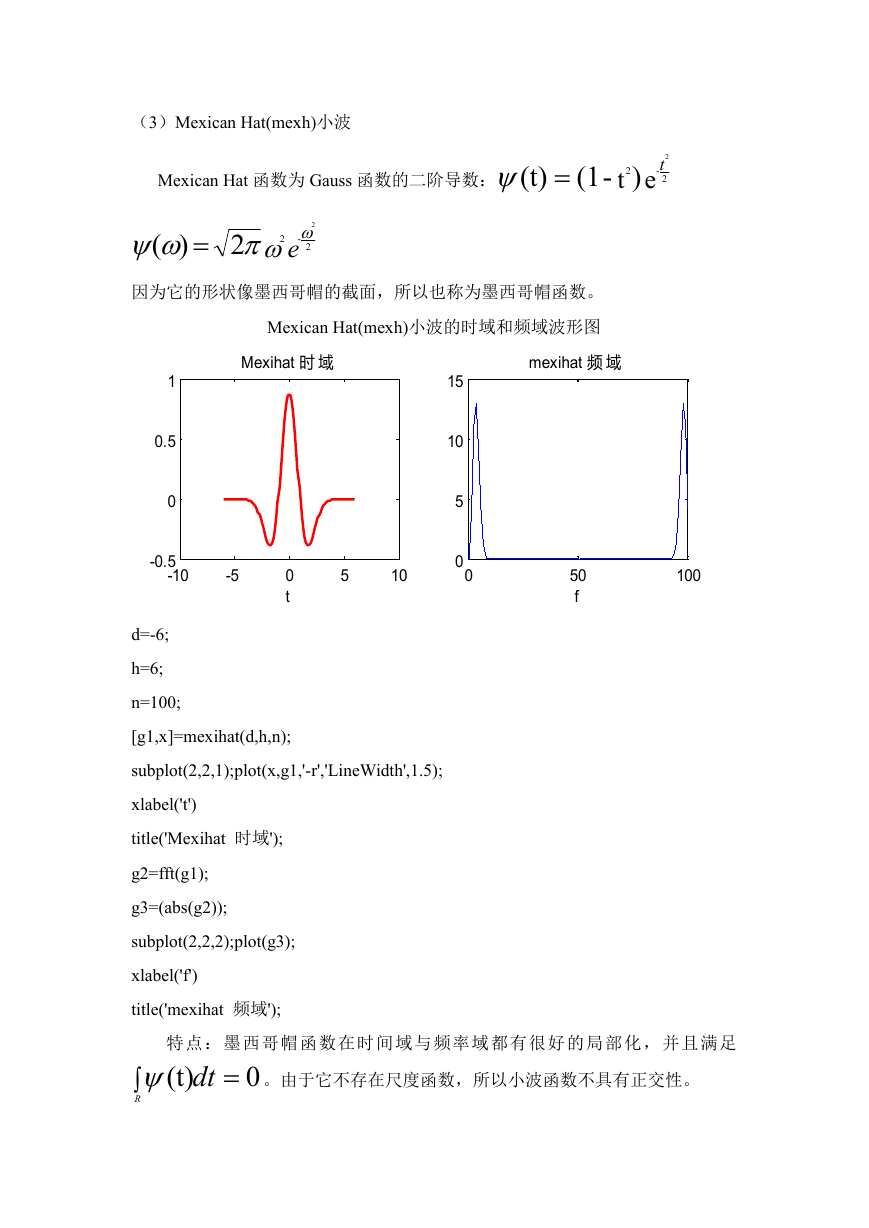
（3）Mexican Hat(mexh)小波
Mexican Hat 函数为 Gauss 函数的二阶导数：
(t)
-(1
2
t
2
2
)
et
-
e 2
)(
2
2
-
2
因为它的形状像墨西哥帽的截面，所以也称为墨西哥帽函数。
Mexican Hat(mexh)小波的时域和频域波形图
mexihat 频 域
50
f
100
15
10
5
0
0
Mexihat 时 域
1
0.5
0
-0.5
-10
-5
5
10
0
t
d=-6;
h=6;
n=100;
[g1,x]=mexihat(d,h,n);
subplot(2,2,1);plot(x,g1,'-r','LineWidth',1.5);
xlabel('t')
title('Mexihat 时域');
g2=fft(g1);
g3=(abs(g2));
subplot(2,2,2);plot(g3);
xlabel('f')
title('mexihat 频域');
特点：墨西哥帽函数在时间域与频率域都有很好的局部化，并且满足
(t)
dt
R
0
。由于它不存在尺度函数，所以小波函数不具有正交性。
（4）Morlet 小波
它是高斯包络下的单频率副正弦函数：
e tC
(t)
-
2
2
cos
(5x)
C 是重构时的归一化常数。Morlet 小波没有尺度函数 (t) ，而且是非正交分解。
Morlet 小波的时域波形图和频域波形图
Morlet 频 域
50
f
100
15
10
5
0
0
Morlet 时 域
1
0.5
0
-0.5
-1
-10
-5
5
10
0
t
d=-6;
h=6;
n=100;
[g1,x]=morlet(d,h,n);
subplot(2,2,1);plot(x,g1,'-r','LineWidth',1.5);
xlabel('t')
title('Morlet 时域');
g2=fft(g1);
g3=abs(g2);
subplot(2,2,2);plot(g3);
xlabel('f')
title('Morlet 频域')
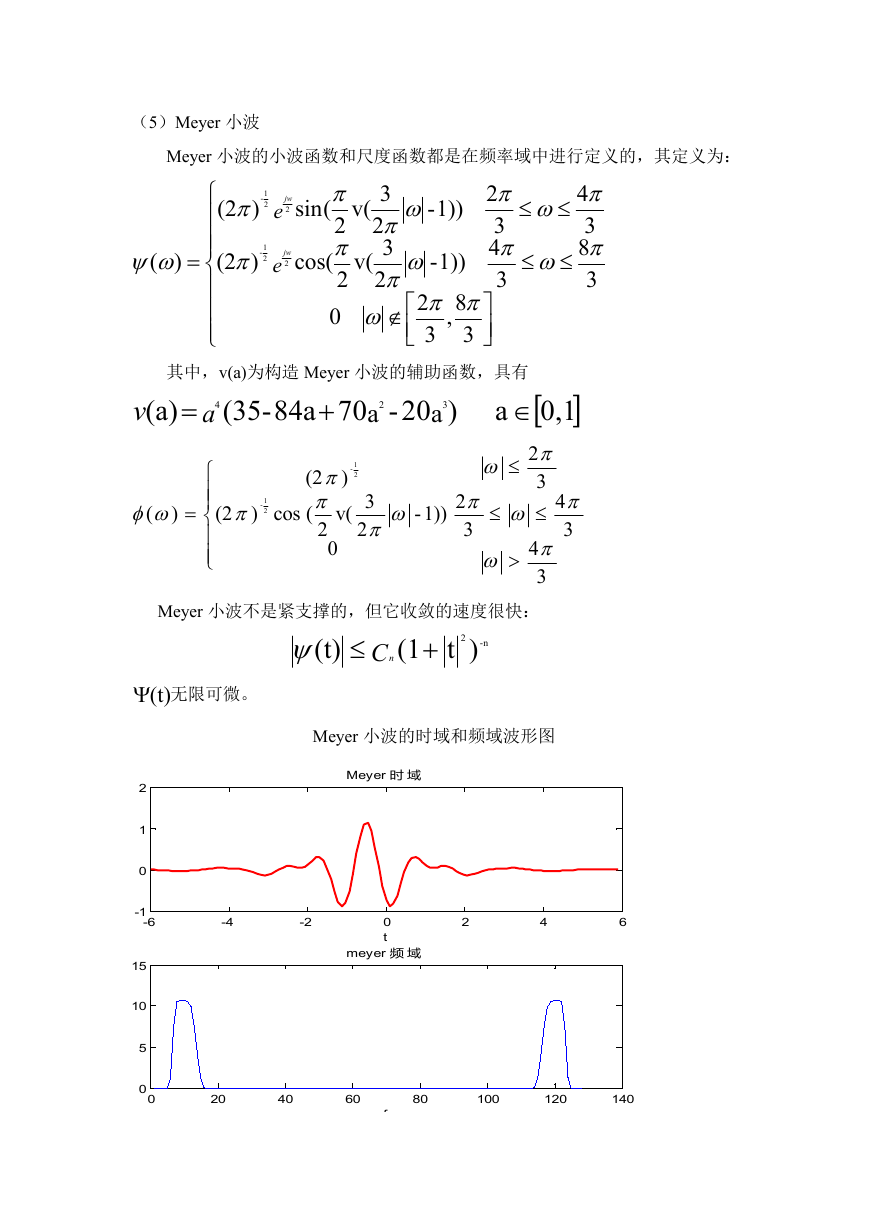
（5）Meyer 小波
Meyer 小波的小波函数和尺度函数都是在频率域中进行定义的，其定义为：
)
jw
2
sin
e
1-
2
1-
2
)
(
)
jw
2
e
cos
(2
(2
2
3
4
3
4
3
8
3
1))
-
3v(
(
2
2
3v(
(
1))
-
2
2
2
8,
0
3
3
(a)
v
4
-
1-
2
3
a
2
a
70
(35
84a
20-
a
)
其中，v(a)为构造 Meyer 小波的辅助函数，具有
0,1
a
2
3
4
3
Meyer 小波不是紧支撑的，但它收敛的速度很快：
(2
)
3v(
(
2
2
0
2
3
(2
)
4
3
-
1))
cos
1-
2
)
(
(t)
C n
(1
n-
2)t
(t) 无限可微。
Meyer 小波的时域和频域波形图
Meyer 时 域
-4
-2
0
t
meyer 频 域
2
4
6
20
40
60
f
80
100
120
140
2
1
0
-1
-6
15
10
5
0
0
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
