第1页 / 共28页
第2页 / 共28页
第3页 / 共28页
第4页 / 共28页
第5页 / 共28页
第6页 / 共28页
第7页 / 共28页
第8页 / 共28页
《信息安全原理与技术》完整版习题答案.pdf
《信息安全原理与技术》习题参考答案
郭亚军，宋建华，李莉
清华大学出版社
第 1 章
1.1 主动攻击和被动攻击是区别是什么？ 答：被动攻击时系统的操作和状态不会改变，因此
被动攻击主要威胁信息的保密性。主动攻 击则意在篡改或者伪造信息、也可以是改变系统的
状态和操作，因此主动攻击主要威胁信息 的完整性、可用性和真实性。
1.2 列出一些主动攻击和被动攻击的例子。 答：常见的主动
攻击：重放、拒绝服务、篡改、伪装等等。
常见的被动攻击：消息内容的泄漏、流量分析等等。
1.3 列出并简单定义安全机制的种类。 答：安全机制是阻止安全攻击及恢
复系统的机制，常见的安全机制包括：
加密机制：加密是提供数据保护最常用的方法，加密能够提供数据的保密性，并能对其
他安全机制起作用或对它们进行补充。
数字签名机制：数字签名主要用来解决通信双方发生否认、伪造、篡改和冒充等问题。
访问控制机制：访问控制机制是按照事先制定的规则确定主体对客体的访问是否合法，
防止未经授权的用户非法访问系统资源。 数据完整性机制：用于保证数据单元完整性的各
种机制。 认证交换机制：以交换信息的方式来确认对方身份的机制。 流量填充机制：
指在数据流中填充一些额外数据，用于防止流量分析的机制。 路由控制机制：发送信
息者可以选择特殊安全的线路发送信息。 公证机制：在两个或多个实体间进行通信
时，数据的完整性、来源、时间和目的地等内
容都由公证机制来保证。
1.4 安全服务模型主要由几个部分组成，它们之间存在什么关系。 答：安全服务是加强数据
处理系统和信息传输的安全性的一种服务，是指信息系统为其应用 提供的某些功能或者辅
助业务。安全服务模型主要由三个部分组成：支撑服务，预防服务和 恢复相关的服务。
支撑服务是其他服务的基础，预防服务能够阻止安全漏洞的发生，检测与恢复服务主要
是关于安全漏洞的检测，以及采取行动恢复或者降低这些安全漏洞产生的影响。
1.5 说明安全目标、安全要求、安全服务以及安全机制之间的关系。
答：见图 1.4，全部安全需求的实现才能达到安全目标，安全需求和安全服务是多对多的关
系，不同的安全服务的联合能够实现不同的安全需求，一个安全服务可能是多个安全需求的
组成要素。同样，安全机制和安全服务也是多对多的关系，不同的安全机制联合能够完成不
同的安全服务，一个安全机制也可能是多个安全服务的构成要素。
1.6 说明在网络安全模型中可信的第三方所起的作用。 答：要保证网络上信息的安全传输，
常常依赖可信的第三方，如第三方负责将秘密信息分配 给通信双方，或者当通信的双方就
关于信息传输的真实性发生争执时，由第三方来仲裁。
1
第 2 章
2.1、列出小于 30 的素数。
2、3、5、7、11、13、17、19、23、29
2.2、若 a 是大于 1 的整数, 则 a 的大于 1 的最小因子一定是素数。
证明 若 a 是素数, 显然 a 的大于 1 的最小因子就是素数 a; 若 a 是合数, 则显然除 1 和 a
外还有其它的因数，令 b 是这些正因数中最小者, 可以证明 b 不是合数而是素数, 若
其不然, b 必有大于 1 且不等于 b 的因数 c, 于是由 c|b 和 b|c 可知 c|a, 即 c 是 a 的因数,
又有 1
证明：由于53 13 mod 56, 56 mod 56
1mod 56, 对同余式两边同时升到10次幂，即那么
(53
53 ) mod 56
(13 13) mod 56
560mod 56
644444444170组444444448
(56 mod 56) (56 mod 56) ......(56 mod 56) mod 56
64444444170组44444448
(1mod 56) (1mod 56) ......(1mod 56) mod 56 1mod 56, 所以
1。
560 mod 56 1mod 56, 从而可以写成560 1mod 56或56|560
所以560 1是56的倍数。
2.6、对于整数 39 和 63，回答下面问题
(1) 它们是否互素；
解：由于 gcd(39,63)=3,所以他们不互素。
(2) 用欧几里德算法求它们的最大公因子；
解：用欧几里德算法的计算过程如下：
63 1 39 24
39 1 24 15
24 1 15 9
15 1 9 6
9 1 6 3
6 2 3 0
所以39和63的最大公因子是3
(3) 25-1 ≡ x mod 15 是否有解。
解：由欧几里德算法有：
25 1 15 10
15 1 10 5
10 2 5 0, 可知25和15的最大公因子是5，即gcd(25,15)=5 1.所以不互素
那么25-1
x mod15无解。
2.7、用欧几里德算法求 gcd (1997, 57)和 gcd(24140, 16762)
3
解：对1997和57运用欧几里德算法的过程如下：
1997 35 57 2
57 28 2 1
2 2 1 0, 所以gcd(1997, 57) 1
同理，对24140和16762运用欧几里德算法的过程如下
24140 1 16762 7378
16762 2 7378 2006
7378 3 2006 1360
2006 1 1360 646
1360 2 646 68
646 9 68 34
68 2 34 0，所以gcd(24140,16762) 34
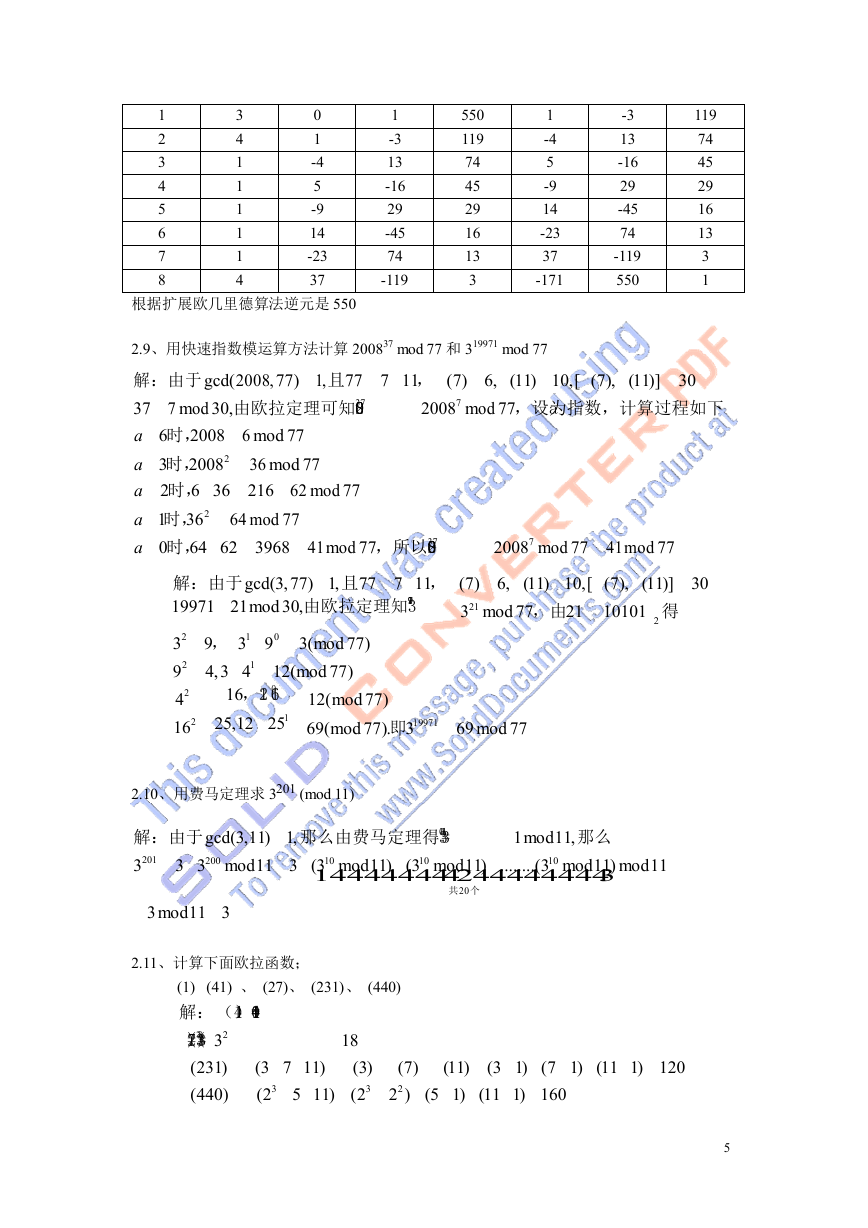
2.8、用扩展欧几里德算法求下列乘法逆元
(1) 1234 mod 4321 用扩展欧几里德算法
的计算过程如下：
循环次数
初始值
1
2
3
4
5
Q
---
3
1
1
153
1
X1
1
0
1
-1
2
-307
X2
0
1
-3
4
-7
1075
1082 3239 mod 4321, 所以逆元是3239
循环次数
初始值
(2) 24140 mod 40902
用扩展欧几里德算法的计算过程如下：
X2
0
1
-1
2
-5
14
-19
52
-487
1
2
3
4
5
6
7
8
根据扩展欧几里德算法没有逆元。
（3）550 mod 1769
Q
---
1
1
2
3
1
2
9
2
X1
1
0
1
-1
3
-10
13
-36
326
X3
4321
1234
619
615
4
3
X3
40902
24140
16762
7378
2006
1360
646
68
34
Y1(T1)
0
1
-1
2
-307
309
Y1(T1)
0
1
-1
3
-10
13
-36
326
-688
Y2(T2)
1
-3
4
-7
1075
-1082
Y2(T2)
1
-1
2
-5
14
-19
52
-487
1026
Y3(T3)
1234
619
615
4
3
1
Y3(T3)
24140
16762
7378
2006
1360
646
68
34
0
解：计算过程如下表所示：
循环次数
X1
初始值
1
Q
--
X2
0
X3
1769
Y1(T1)
0
Y2(T2)
1
Y3(T3)
550
4
1
2
3
4
5
6
7
8
3
4
1
1
1
1
1
4
0
1
-4
5
-9
14
-23
37
1
-3
13
-16
29
-45
74
-119
550
119
74
45
29
16
13
3
1
-4
5
-9
14
-23
37
-171
-3
13
-16
29
-45
74
-119
550
119
74
45
29
16
13
3
1
根据扩展欧几里德算法逆元是 550
(7) 6, (11) 10,[ (7), (11)] 30
20087 mod 77，设a为指数，计算过程如下
2.9、用快速指数模运算方法计算 200837 mod 77 和 319971 mod 77
解：由于gcd(2008, 77) 1, 且77 7 11，
37 7 mod 30,由欧拉定理可知200837
a 6时，2008 6 mod 77
a 3时，20082
a 2时，6 36 216 62 mod 77
a 1时，362
a 0时，64 62 3968 41mod 77，所以200837
36 mod 77
64 mod 77
解：由于gcd(3, 77) 1, 且77 7 11， (7) 6, (11) 10,[ (7), (11)] 30
19971 21mod 30,由欧拉定理知319971
321 mod 77，由21 10101 得
2
20087 mod 77 41mod 77
32 9， 31 90 3(mod 77)
92 4, 3 41
42
162
16，12 160
25,12 251
12(mod 77)
12(mod 77)
69(mod 77).即319971
2.10、用费马定理求 3201 (mod 11)
69 mod 77
1mod11, 那么
解：由于gcd(3,11) 1, 那么由费马定理得310=311-1
3201
3 3200 mod11 3 (310 mod11) (310 mod11) ........(310 mod11) mod11
1444444442444444443
共20个
3 mod11 3
2.11、计算下面欧拉函数；
(1) (41) 、 (27)、 (231)、 (440)
解： （41）=41-1=40
(27)=(33)=33 32
(231)
(440)
(3 7 11)
5 11)
(23
18
(3)
(23
(11)
(7)
22 ) (5 1) (11 1) 160
(3 1) (7 1) (11 1) 120
5
(2) φ(2)φ(6)和 φ(3)φ(4)，哪一个等于 φ(12)。
解： (2) (6)
(3) (4)
(12)
(3) 1 1 2 2
2) 4
(3) (22 ) 2 (22
(3) (22 ) 2 (22
(3 22 )
2) 4
(2)
(2)
显然 (3) (4)
(12)
2.12、求解下列一次同余方程
(1)3x≡10(mod 29)
解 因为(3，29)＝1，所以方程有惟一解。利用辗转相除法求得使 3x＋29y＝1 成立的 x、y
为 x＝10，y＝－1。于是 3·10＋29·(－1)＝1，3·100＋29·(－10)＝10，所以 x≡100≡13(mod 29)。
(2)40x≡191(mod 6191)
解 因为(40，6191)＝1，所以方程有惟一解。利用辗转相除法求得使 40x＋6191y＝1 成立的
x、y 为 x＝1393，y＝－9。于是 40·1393＋6191·(－9)＝1，40·1393·191＋6191·(－9·191)＝191，
所以 x≡1393·191≡6041(mod 6191)
(3)258x≡131(mod 348)
解 因为(258， 348)＝6，而 6 131，所以方程无解。
2.13、证明下面结论
设 a、b、c、d 为整数，m 为正整数，若 a≡b(mod m)，c≡d(mod m)，则：
(1)ax＋cy≡bx＋dy(mod m)，x、y 为任意整数；
(2)ac≡bd(mod m)；
(3)an≡bn(mod m)，n＞0；
(4)f(a)≡f(b)(mod m)，f(x)为任一整系数多项式。
证明 (1)因为 a≡b(mod m)，c≡d(mod m)，所以 m|(a－b)，m|(c－d)，于是 m|((a－b)x＋(c
－d)y)，即 m|((ax＋cy)－(bx＋dy))，故 ax＋cy≡bx＋dy(mod m)。
(2)因为 a≡b(mod m)，c≡d(mod m)，所以 m|(a－b)，m|(c－d)，于是 m|((a－b)c＋(c－d)b)，
即 m|(ac－bd)，故 ac≡bd(mod m)。
(3)因为 a≡b(mod m)，则存在整数 q 使得 a－b＝mq。于是： an－bn＝(b＋mq)n－bn＝(bn＋
bn-1(mq)1＋…＋b1(mq)n-1＋(mq)n)－bn＝mp，其中 p 是一整 数。
所以 an≡bn(mod m)。
(4)由(1)和(3)可证。
2.14、求满足下面同余方程的解
x≡1(mod 5)，x≡5(mod 6)，x≡4(mod 7)，x≡10(mod 11)
解：令 m1＝5，m2＝6，m3＝7，m4＝11，b1＝1，b2＝5，b3＝4，b4＝10。则 m＝2310，M1
＝462，M2＝385，M3＝330，M4＝210。 利用辗转相除法求得 M1 ＝－2，
M2 ＝1，M3 ＝1，M4 ＝1。 所以，x≡1·(－2)·462＋5·1·385＋ 4·1·330＋
10·1·210≡4421≡2111(mod 2310)
2.15、求 Z5 中各非零元素的乘法逆元。
解：1-1=1,2-1=3,3-1=2,4-1=4
6
2.16、类似于表 2.2，用表列出有限域 GF(5)中的加法和乘法运算
解：表如下：
2
2
3
4
0
1
2
0
2
4
1
3
3
3
4
0
1
2
3
0
3
1
4
2
4
4
0
1
2
3
4
0
4
3
2
1
0
0
1
2
3
4
0
0
0
0
0
0
-a
0
4
3
2
1
1
1
2
3
4
0
1
0
1
2
3
4
a-1
--
1
3
2
4
加法
0
1
2
3
4
乘法
0
1
2
3
4
a
0
1
2
3
4
2.17、对于系数在 Z10 上的取值的多项式运算，分别计算
a
x+2)-(x2+5)=-x2+7x-3mod(10x2+10x+10)=9x2+7x+7
b、(6 x2
5x3
x 3) (5x2 2)
7 x2
2x 6
(30 x4 5x3 27 x2 2x 6) mod(10x4 5x3 27 x2 2x 6)
2.18、假设 f(x)=x3+x+1 在 GF(2n)中是一个不可约多项式，a(x)=2x2+x+2,b(x)=2x2+2x+2,求
a(x)b(x)
解：a(x) b(x)=a(x)b(x)modf(x) (2x2+x+2)(2x2+2x+2)mod（x3+x+1）
=6x3+6x2+2x+4
2.19、编程实现模 n 的快速指数运算。
#include "stdafx.h"
#include
#include
int main(int argc, char* argv[])
{
int m,e,n;
printf("input the first number: ");
cin>>e;
7
printf("input the second number: ");
cin>>m;
printf("input the third number: ");
cin>>n;
int a=e,b=m,c=1;
for(a=e;a>0; )
{
if(a%2==1)
{
a-=1;
c=(c*b)%n;
if(a==0)
cout<
int main(int argc, char* argv[])
{
first number:"<>m;
cout<<"input the second number:"<>d;
int a[3]={1,0,m},b[3]={0,1,d};
int Q;
if(b[2]%a[2]>=0)
{
Q=b[2]/a[2];
for(int i=0;i<=2;i++)
{
t[3];
int
t[i]=a[i]-Q*b[i];
a[i]=b[i];
b[i]=t[i];
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
