logo资料库

选主元的Gauss消去法和不选主元的Gauss消去法实验报告含源码.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.18M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    课程实验报告 课程名称 数值分析 班级 实验日期 2008 年 9 月 30 日 姓名 实验名称 学号 实验成绩 实验四 Gauuss 列主元消去法解线性方程组 实 验 目 的 及 要 求 实 验 环 境 实 验 内 容 实验目的： 1．熟悉 Gauss 列主元消去法，编出实用程序。 2．认识选主元技术的重要性。 3．明确对于哪些系数矩阵 A ，在求解过程中不需使用选主元技 术。 实验要求： 1．编制程序，用 Gauss 列主元消去法求解线性方程组 Ax b ， 并打印结果，其中 （1） A （2） A 3   3.712 4.623   1.072 5.643  2 810    1    2  4 4   2 17 10    4 10 9  2       ， ， b b 1     2       3 10     3      7  2．与不选主元的 Gauss 消去法结果比较并分析原因。 Windows xp 操作系统 VC++6.0 可以清楚地看到，若 ( 过程继续下去。有时既使 ( 由解一般线性方程组在使用 Gauss 消去法求解时，从求解过程中 kka   ，必须施以行交换的手续，才能使消去 kka   ，但其绝对值很小，由于舍入误差 的影响，消去过程也会出现不稳定现象。因此，为使这种不稳定现象 0 1) k 0 1) k 发生的可能性减至最小，在施行消去过程时每一步都要选主元素，即 要寻找行 r ，使 1)  | a ( k rk | max |  i k  1)  ( k a ik | 并将第 r 行与第 k 行交换，以使 ( 于 0。 k 1) kka  的当前值（即 ( ika  的数值）远大 k 1)
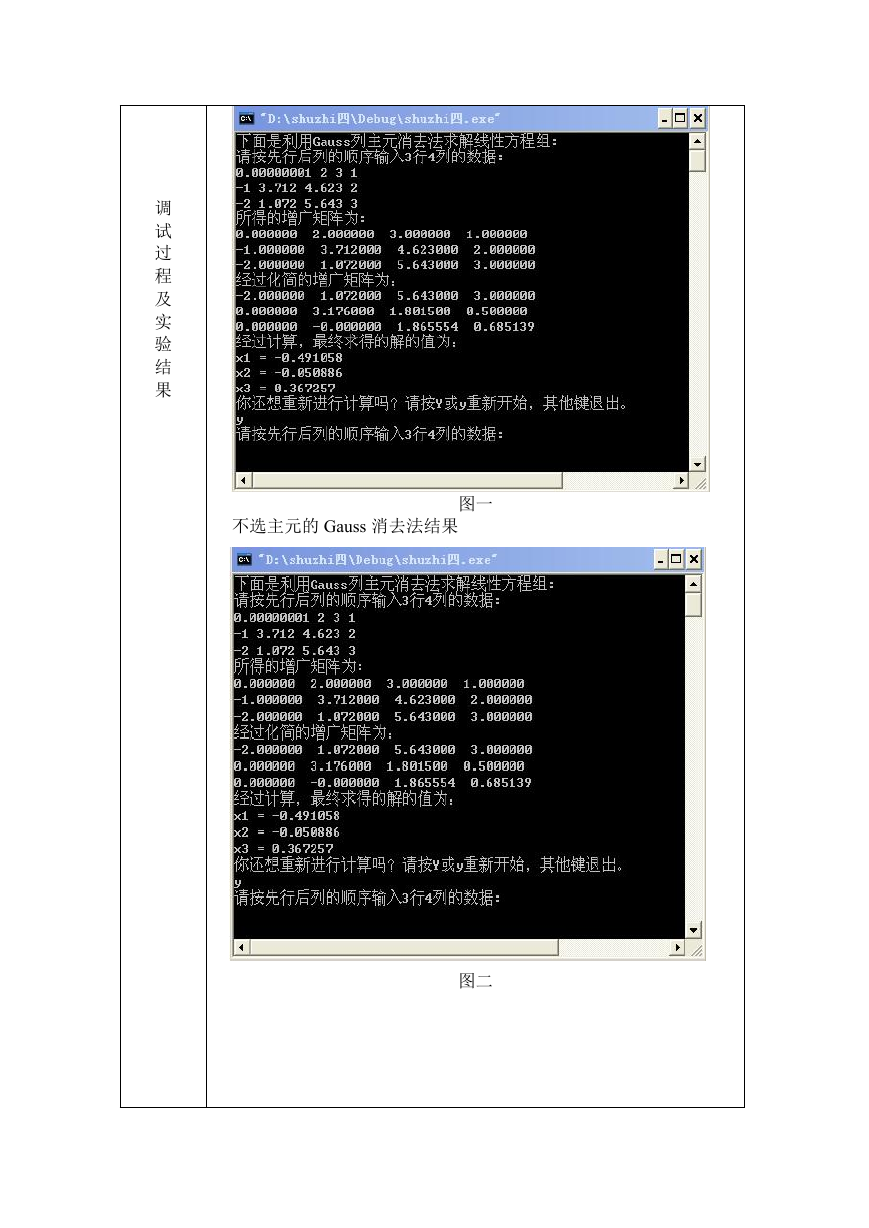
    这种列主元消去法的主要步骤如下： 1．消元过程 对 1,2, n  1º 选主元，记 ，做 1  k , | a rk | max |  i k  a ik | 若 rka  ，说明方程组系数矩阵奇异，则停止计算，否则进行 2 0 º。 2º 交换 A （增广矩阵）的 ,r k 两行元素 a rj  a kj j  k ,  n , 1 3º 计算 a ij  a ij  a a ik kj / a kk i    1, k , n j   k 1,  n , 1 2．回代过程 , n n 对  k 1,   ，计算 ,2,1 x k  ( a , k n 1  n   1 j k   a x kj j / a kk ) 实验步骤： 1、程序设计 2、计算实例 3、撰写实验报告 算 法 描 述 及 实 验 步 骤 1、实验 1 的运行结果如图 用 Gauss 列主元消去法求解线性方程组
    调 试 过 程 及 实 验 结 果 不选主元的 Gauss 消去法结果 图一 图二
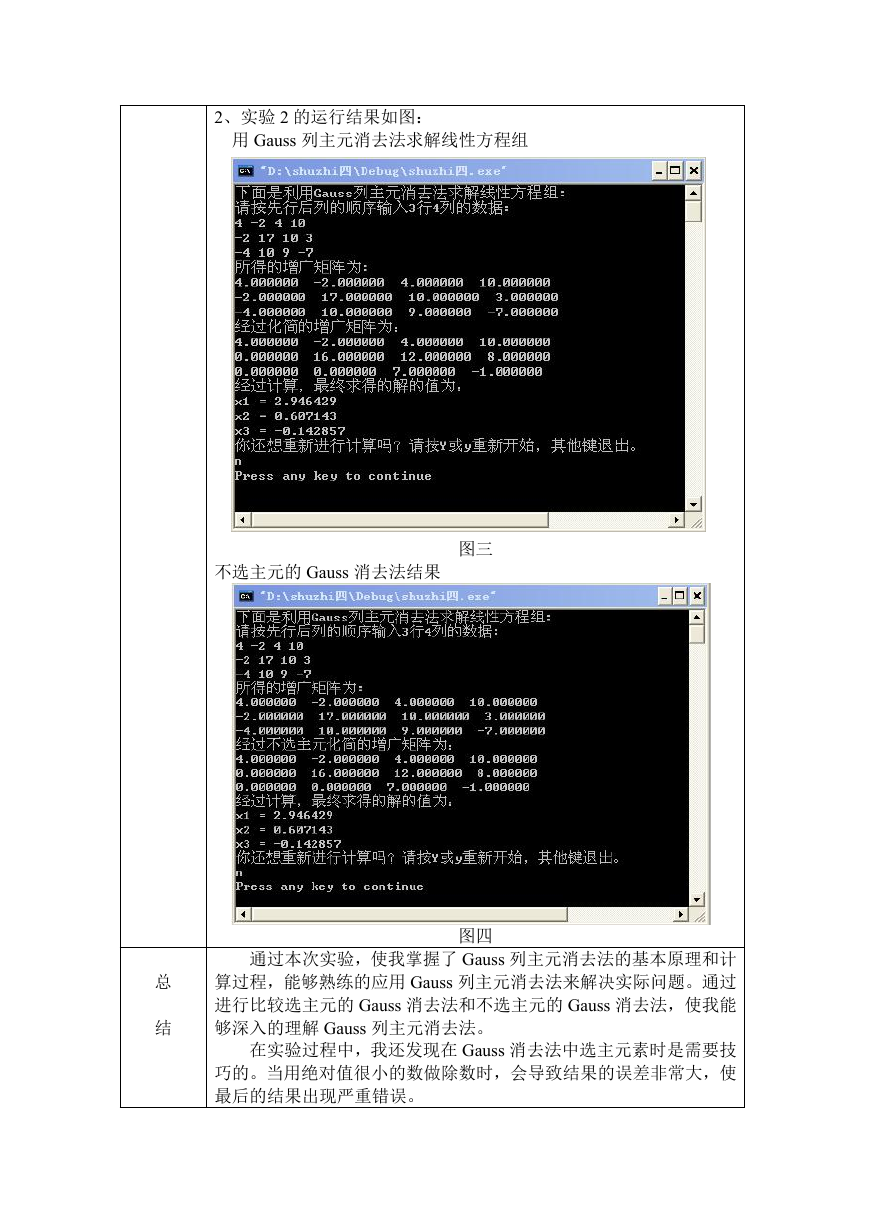
    2、实验 2 的运行结果如图： 用 Gauss 列主元消去法求解线性方程组 不选主元的 Gauss 消去法结果 图三 图四 总 结 通过本次实验，使我掌握了 Gauss 列主元消去法的基本原理和计 算过程，能够熟练的应用 Gauss 列主元消去法来解决实际问题。通过 进行比较选主元的 Gauss 消去法和不选主元的 Gauss 消去法，使我能 够深入的理解 Gauss 列主元消去法。 在实验过程中，我还发现在 Gauss 消去法中选主元素时是需要技 巧的。当用绝对值很小的数做除数时，会导致结果的误差非常大，使 最后的结果出现严重错误。
    附 录 1.列主元素消去法 #include #include #include using namespace std; #define row 3 #define list 4 float a[row][list]; void display(); int get_mainelement(int j); void change(int m,int n); void account(int m,int n); void main() { char A; cout<<"下面是利用 Gauss 列主元消去法求解线性方程组:"<
    if(i!=i+y) { account(i,i+y); y++; } else } } y++; cout<<"经过化简的增广矩阵为："<>A; }while(A=='Y'||A=='y'); } void display()//显示函数 { for(int i = 0 ;i<=row-1;i++) { for(int j = 0;j<=list-1;j++) {
    ",a[i][j]); printf("%f } cout<
    2．不选主元的 Gauss 消去法 #include #include #include using namespace std; #define row 3 #define list 4 float a[row][list]; void display(); void account(int m,int n); void main() { char A; cout<<"下面是利用 Gauss 列主元消去法求解线性方程组:"<
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料