Tera-Hertz Wave Amplification vis Relativistic Electrons Pumped ....pdf-资料库

中国科技论文在线 http://www.paper.edu.cn Tera-Hertz Wave Amplification vis Relativistic Electrons Pumped by a Planar Electrostatic System 1 Shi-Chang Zhang* Institute of Photoelectronics Southwest Jiaotong University Chengdu, P. R. China610031 sczhang@home.swjtu.edu.cn Abstract A mechanism of Tera-Hertz wave amplification is proposed, where a planar electrostatic pumps the kinetic energy of relativistic electrons to the wave. The planar electrostatic system is formed by two parallel metallic plates, where the super-plate is corrugated with sinusoidal ripples and connected to a negative voltage while the sub-plate is smooth and grounded. The relativistic Doppler up-shift frequency and gain of the wave are derived in detail. 1 I n t r o d u c t i o n In the past years, the free-electron laser (FEL) has been widely investigated as a new kind of coherent radiation sources 1-10. Compared to the ordinary lasers, it has an attractive peculiarity that the frequency is tunable from microwave to x-ray, especially in the far-infrared range and x-ray 11, 12. Physically speaking, a FEL is based on the coherent radiation simulated by relativistic free electrons in a magneto-static system (referred to as the wiggler or undulator) in which the magnets are alternatively arranged so as to let the magnetic field have a sinusoidal distribution. In this periodical magnetic field, relativistic electrons move along approximately sinusoidal trajectories, and it is the periodic-varying motion of the relativistic electrons that results in the electromagnetic emission. After the pioneer operation of the first free-electron laser experiment at Stanford University 2, two other kinds of proposed wigglers emerged, which were expected to play similar role as a magneto-static wiggler does. One is refereed to as the electromagnetic-wave wiggler, where an external electromagnetic wave is injected into the interaction range and its components with sinusoidal variation in space and time govern the relativistic electrons 13. The other is the so-called electrostatic wiggler either by using a ring-loaded waveguide where the rings are insulated from each other and alternatively connected to a positive/negative voltage 14, or by utilizing a large potential drop of the electron beam to the wall corrugated with ripples 15. As was pointed out in Ref. [15], in fact, wave amplification in an electrostatic system with a rippled cylindrical tube is by no means new. Previously, wave amplification was performed by utilizing the 1 Support by the China University-College PhD Science Foundation (No. 200806130012) and the NSFC (no. 60871023). 1

中国科技论文在线 http://www.paper.edu.cn slow-wave modes16-18, or non-relativistic electron beam19, 20, or space-charge waves15, 21, 22. Generally speaking, a slow-wave structure is complicated; use of non-relativistic electron beam obstructs the output power; and effect of the space-charge wave needs high-current electron beam. Perhaps due to these restrictions, unfortunately, studies of wave amplification in an electrostatic system with corrugated periodic ripples have been ceased since then on. Up to date main interest in the corrugated periodic-ripples structure is concentrated on the application as Bragg reflectors to constructing high-Q cavities for the cyclotron autoresonance maser (CARM) and free-electron laser oscillators23-41. To the best of my knowledge, field distribution in an electrostatic system with corrugated periodic-ripples boundary was not analytically derived before. Recently, analytical derivation demonstrated that a planar electrostatic system with sinusoidal ripples can efficiently modulate relativistic electrons just as a magnetostatic wiggler (or undulator) does in FEL42. Here the planar electrostatic system is performed by two parallel metallic plates: the super-plate is corrugated with sinusoidal ripples and connected to a negative voltage; the sub-plate is smooth and grounded. Unlike the works before, the present paper is devoted to the amplification mechanism of a fast wave by a relativistic electron beam in a planar electrostatic system, where the space-charge effect is excluded. Results will show that the amplification mechanism is quite suitable for a mild relativistic electron beam to generate Terahertz wave. Organization of this paper is as follows. In Sec. II the motion of relativistic electron in the planar electrostatic system is calculated. Comparison will show that this planar electrostatic system plays a similar role as a magneto-static wiggler in a FEL in governing the electrons’ motion. Dynamic behavior of a single electron in the interaction with electromagnetic wave is studied in Sec. III. Amplification gain of the electromagnetic wave is derived in Sec. IV. Finally, discussion and conclusions are drawn in Sec. V. 2 M o d u l a t e d M o t i o n o f R e l a t i v i s t i c E l e c t r o n s The profile of a planar electrostatic system is shown in Fig. 1, where two parallel metallic plates are : the sub-plate is smooth and grounded; the super-plate is connected separated from a mean distance h to a negative voltage 0V and corrugated with sinusoidal ripples (the ripple period and the ripple depth p and l , respectively). Figure 2 shows a Cartesian coordinates system ( , x y z to be adopted in being the present paper. The boundary function of the super-plate with sinusoidal ripples can be expressed by , ) where x sup h l cos( kz ) , (1) k 2 p . (2) Before deriving the beam-wave interaction, it is worthy to review the modulated motion of a relativistic electron in the planar electrostatic system. Assume that the width in the y-direction and the length in the z-direction of the system are much greater than the height in the x-direction. Then the electrostatic potential satisfies the two-dimensional Laplace equation and electrostatic field in the system can be mathematically manipulated42: E x z ( , ) x V 0 h V k l h 0 ( / sh kh ( ) ) ch kx cos( kz ) , (3) E x z ( , ) z V k l h 0 ( / sh kh ( ) ) sh kx sin( kz ) , (4) 2

中国科技论文在线 http://www.paper.edu.cn yE x z , (5) ( , ) 0 where ch kx ( ) is the hyperbolic cosine function. Expanding sh ( ) 5 3 5 3 and ch ( ) 1 and (4) as 4 2 4 2 close to the super-plate region, one may approximate Eqs. (3) 1 E x z ( , ) x V 0 h V l 0 2 h cos( kz ) , (6) E x z ( , ) z V kl 2 0 h x sin( kz ) . (7) Comparison with the CST simulation results shows that Eqs. (6) and (7) are good estimation of (3) and (4) 42, and therefore, for the simplicity of calculation we shall use Eqs. (6) and (7) in the following derivation. Obviously, if the super-plate is not corrugated with sinusoidal ripples, then and all the above expressions come back to those of a smooth structure. Here we can see that the terms with sine or cosine functions reflect the effect of the periodic boundary on the field. l 0 Figure 1: Longitudinal-section view of a planar electrostatic system, where the super-plate of two parallel metallic plates is corrugated with sinusoidal ripples and connected to a negative voltage while the sub-plate is smooth and grounded. 3

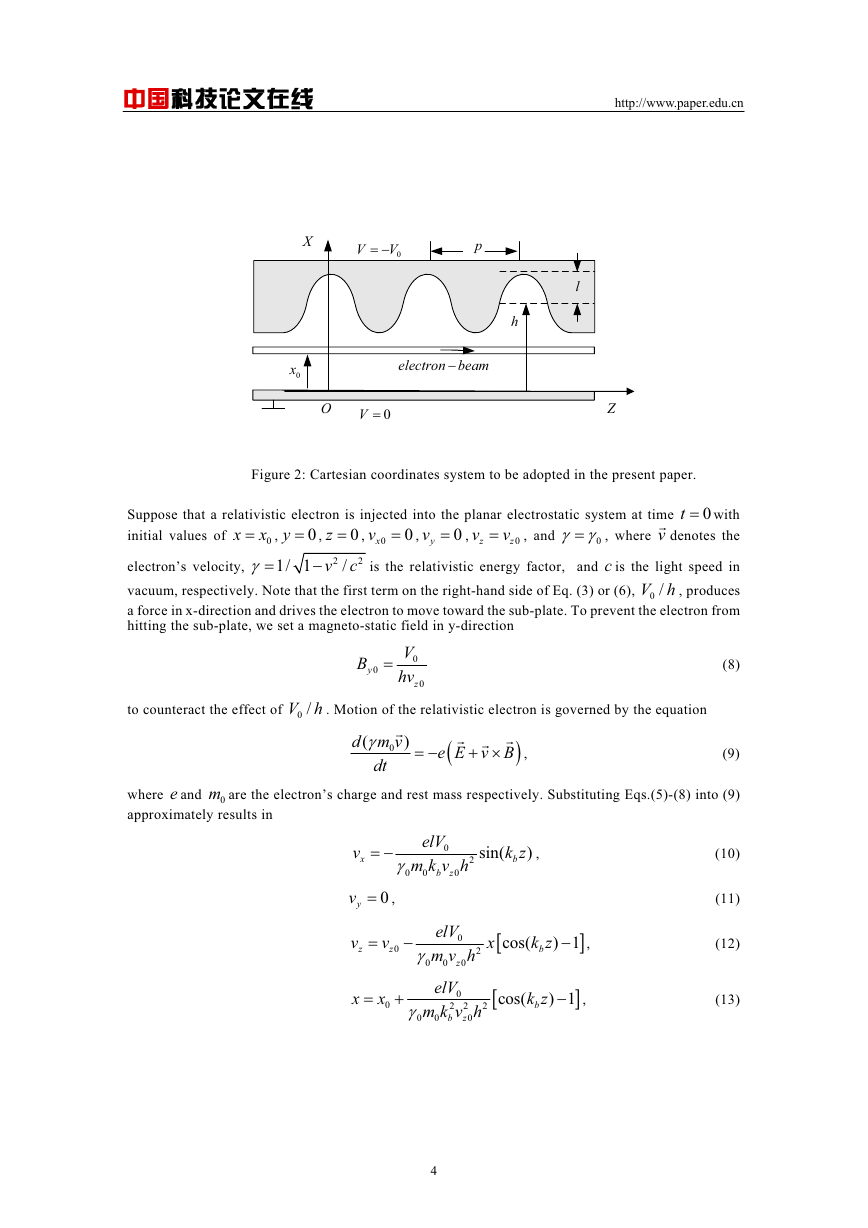
中国科技论文在线 http://www.paper.edu.cn X V V 0 p l h 0x electron beam O 0V Z Figure 2: Cartesian coordinates system to be adopted in the present paper. Suppose that a relativistic electron is injected into the planar electrostatic system at time initial values of x x 0 , y 0 , z 0 , xv , 0 0 yv , 0 v z v z 0 , and 0 t 0 with , where v denotes the electron’s velocity, 1/ 1 2 /v c 2 is the relativistic energy factor, and c is the light speed in vacuum, respectively. Note that the first term on the right-hand side of Eq. (3) or (6), 0 /V h , produces a force in x-direction and drives the electron to move toward the sub-plate. To prevent the electron from hitting the sub-plate, we set a magneto-static field in y-direction to counteract the effect of 0 /V h B y 0 V 0 hv z 0 (8) . Motion of the relativistic electron is governed by the equation d m v 0 ( dt ) e E v B , (9) where e and approximately results in 0m are the electron’s charge and rest mass respectively. Substituting Eqs.(5)-(8) into (9) v x 0 elV 0 m k v h b z 0 0 sin( k b 2 z , (10) ) yv , (11) 0 v z v z 0 0 elV 0 m v h z 0 0 x 2 cos( k z b , (12) ) 1 x x 0 0 elV 0 m k v h 2 2 b z 0 0 2 cos( k z b , (13) ) 1 4

中国科技论文在线 http://www.paper.edu.cn z v t 0 z 0 elV x 0 0 2 2 b z 0 m k v h 0 sin( k z b ) 2 . (14) As is derived [seeing Eqs.(2.1), (2.5) and (2.6) in Ref. 3], in a FEL the magnetic field of a linearly polarized wiggler yB z ( ) 2 B sin( k 0 z (15) ) forces a relativistic electron to move with v x 2 z 0 v 0 0 cos( )k z 0 , (16) v z v z 0 x 2 z 0 2 2 0 2 2 0 v 4 zv 0 2 0 0 cos(2 k z 0 ) , (17) sin( k z 0 ) , (18) z v t 0 z z 0 2 v 4 2 0 3 0 sin(2 k z 0 ) , (19) 2 / B and k 0zk v are the amplitude and normalized amplitude of the wiggler magnetic field, where we realize that a planar electrostatic system plays a similar role just as a magneto-static wiggler does in modulating relativistic electrons. is the period of the wiggler. Comparing Eqs. (10)-(14) to (16)-(19), , and 0l l 0 , 0 0 0 3 E n e r g y t r a n s f e r f r o m R e l a t i v i s t i c E l e c t r o n s t o W a v e Now we introduce a circularly polarized electromagnetic wave traveling parallel to the electron: w E B w ˆ e E x m sin( k z w t ) ˆ e E y m cos( k z w t ) (20) ˆ e E x m w k cos( k z w t ) ˆ e E y m w k sin( k z w t ) (21) where ˆxe and ˆye are the unit vectors in x- and y-directions, mE , wk , and are the wave amplitude, wave-number and angular frequency, respectively. In the interaction of the relativistic electron having the velocity expressed by Eqs.(10)-(12) with the wave, the energy change of the electron is in balance of the work done by the wave: 2 ) d m c ( 0 dt ev E . (22) Substituting Eqs.(10)-(12), and (20) into (22) yields d dt 2 0 2 e lV E m 2 0 2 2 0 m c h k v b z cos( k z w t k z b ) cos( k z w t k z b ) . (23) 0 5

中国科技论文在线 http://www.paper.edu.cn Attention should be paid that in Eq. (23) both z and mE are function with respect to time t and the integral is quite complex. Before dealing with the integral, let us examine how to simplify it. If we assume z v t 0z and neglect the change of mE , we integrate Eq.(23) and obtain 0 2 0 2 e lV E m 2 0 2 2 0 m c h k v b z sin 0 k v z k w k k v b w b z 0 t 0 sin k v z k w k k v b w b z 0 t 0 . (24) The left-hand side of Eq. (24) denotes the energy loss of the electron. In order to transfer the electron’s energy to the wave as much as possible, one may choose the denominator on the right-hand side to tend k b v z 0 0 or k w k b leads to a Doppler down-shift frequency to a Doppler up-shift frequency k w v z 0 . Noting that k k w b 0 k b w to zero, that is, k v k v k k k w w z 0 b z 0 b 0 0 v z 0 whereas v z 0 , we choose k w k b v . (25) 0 z 0 In this case the first term in the bracket on the right-hand side of Eq.(24) can be omitted compared to the second term; in other words, backward to Eq. (23), the first term in the bracket on the right-hand side of Eq.(23) can be omitted. Therefore, under the restriction of Eq. (25), Eq. (23) can be simplified as d dt 2 0 2 e lV E m 2 0 2 2 0 m c h k v b z cos( k z w t b k z ) . (26) 0 Using d dz d dt dz dt v z d dz v z 0 d dz , we rewrite Eq. (26) as d dz 2 0 Letting 2 e lV E m 2 0 2 2 0 2 m c h k v b z 0 cos( k z w t b k z ) . (27) ( k w k z b ) t , (28) we further rewrite Eq. (27) as 0 (thus d dz d / / dz ) , (29) d dz 2 0 2 e lV E m 2 0 2 2 0 2 m c h k v b z 0 cos . (30) Noting d dz t dz z dt z 1 v z t , from Eq.(28) we straightforward obtain d dz k w k b v z . (31) 6

中国科技论文在线 http://www.paper.edu.cn One may expand 1 zv as Tyler series of 0 at : 1 v z 1 ( 0 ) v z d 1 d v ( z 0 1 ( 0 ) v z 1 d d v ( ) 0 z 0 ( 0 ( 0 ) 1 2 ) ) 0 2 d d 2 1 ( 0 ) v z 0 ( 0 2 ) 2 1 ( c 3 3 v z 0 ) ( 0 0 = v z ) ( 0 ) , (32) where 1 2 /zv 2 c , 2 z dv c v d 3 z , and have been used. Substituting Eq. (32) into (31), we obtain 0 d 1 d ( ) v z 1 2 z v dv ( ) z d 0 v 3 z 2 c ( ) 0 3 0 d dz k w k b ( 0 ) v z v 3 z Defining the mismatching parameter 2 c ( ) 0 3 0 ) ( 0 . (33) k w k b 0( ) v z (34) and making use of Eq. (29), we rewrite (33) as d dz v 3 z 2 c ( ) 0 3 0 . (35) A pendulum equation can be deduced from Eqs (30) and (35): d 2 dz 2 2 4 0 2 2 c e lV E m 5 m c h k v b z 2 2 0 0 2 0 cos . (36) 0 In the following derivation we shall employ Eq. (36) instead of (35), along with (30), to describe the dynamic behavior and energy loss of the relativistic electron. Comparing Eqs (30), (35), and (36) to the results in a FEL pumped by a magneto-static wiggler [for example, seeing Eqs. (1.11)-(1.13) in Ref.10], one can conclude that here the relativistic electron undergoes same effect as that in a FEL with magneto-static wiggler. 4 G a i n F o r m u l a o f W a v e In this section we consider the wave growth due to the energy gain delivered by the electron beam, where the wave amplitude should be regarded as a function of z , wE z ( ) . The energy exchange between the wave and the electron is governed by the conservation of energy 43: 7

中国科技论文在线 http://www.paper.edu.cn S J E w , (37) u t where and E E w ( 0 0 w u 1 2 H H w ) w , (38) w S E H w (39) are the energy density and Poynting vector of the wave, v en 0 J (40) is the current density of the electron beam, and 0n is the initial bulk density of the electron beam. Substituting Eqs.(10)-(12), (21), and (22) into (38)-(40), and then inserting into (37), we obtain, after straightforward manipulation, that dE z ( ) m dz n lV e 0 0 m k 2 0 0 b 0 z 2 2 h 0 cos , (41) where z 0 zv 0 / c is the normalized axial velocity. Attention should be paid that the energy loss of the whole electron beam should be the average of all the electrons by their phase, and therefore, Eqs.(30), (36) and (41) should be modified as d i 2 dz 2 2 4 0 2 2 c e lV E m 5 m c h k v b z 2 2 0 0 2 0 cos i , (42) 0 d dz i 2 0 2 e lV E m 2 0 2 2 0 2 m c h k v b z 0 cos i , (43) dE z ( ) m dz n lV e 0 0 m k 2 0 0 b 0 z 2 2 h 0 cos i , (44) where i ( k w k b average value means v zo ) z i is the i-th electron’s phase, i [0, 2 ] is its initial phase, and the 1 2 2 0 . (45) ( ) id Now the three independent equations, (42), (43) and (45), form a set of ordinary differential equations, and both the wave amplification determined by mE z ( ) and the energy loss of the electron beam i can be solved from these three equations. Defining the gain of the amplified wave 8

资料库

Tera-Hertz Wave Amplification vis Relativistic Electrons Pumped ....pdf

相关推荐

开发技术

热门标签

最新资料