logo资料库

多约束条件下智能飞行器航迹快速规划研究.pdf

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：2.54M 资料格式：pdf 举报 版权申诉
第1页 / 共37页
第2页 / 共37页
第3页 / 共37页
第4页 / 共37页
第5页 / 共37页
第6页 / 共37页
第7页 / 共37页
第8页 / 共37页
资料共37页，剩余部分请下载后查看
    一、问题重述
    二、问题分析
    三、模型假设
    四、符号说明
    五、模型的建立与求解
    六、模型评价与改进
    七、模型的应用和推广
    八、参考文献
    附 录
    中国研究生创新实践系列大赛 中国研究生创新实践系列大赛 ““华为杯华为杯””第十六届中国研究生 第十六届中国研究生 数学建模竞赛 数学建模竞赛 学 校 重庆大学 参赛队号 19106110065 队员姓名 1. 2. 3. 郑 冬 陈 雲 于婷婷 0
    中国研究生创新实践系列大赛 中国研究生创新实践系列大赛 ““华为杯华为杯””第十六届中国研究生 第十六届中国研究生 数学建模竞赛 数学建模竞赛 题 目 多约束条件下智能飞行器航迹快速规划研究 摘 要 现如今，智能飞行器技术被广泛应用于军事领域及民生领域，为了使飞行器适应复杂 的环境，克服自身系统结构限制，减小在飞行过程中的误差，需要提高其系统定位精度限 制下的航迹快速规划能力。本文是以飞行器的航迹段数及校正次数最少为目标，根据校正 点布局、校正误差约束和 B 点所能接受的最大误差等条件，利用了经典迭代算法和逐步搜 索方法对问题进行求解，得到了优化的航迹路径规划，成功地完成了飞行任务。 关于问题一，首先以校正点到出发点和目的地两点间直线的距离为依据，设置阈值， 对附件中的校正点数据进行筛选，获得备选校正点库 1。基于忽略特殊因素航迹是直线段 的假设，以航迹长度最小化为主要目标，校正点数目最小化为次要目标，讨论首校正点为 垂直校正点和水平校正点两种情况，在校正点处校正条件、目的地处降落条件的约束下， 建立了双目标飞行器航迹规划模型。采用经典迭代方法和权重函数模型逐个搜索最优校正 点，利用 MATLAB 软件对模型进行求解，得到的结果为：（1）附件 1：航线规划路径为 A  503  69  237  155  338  206  340  277  B，第一个校正点是垂直误差校正 点，经过的校正点数目为 8 个，航迹长度为 106467.5307 米；（2）附件 2：航线规划路径 为 A  163 114  8 309 121 123 45  160 92 93 61 292 B，第一个校 正点是水平误差校正点，经过的校正点数目为 12 个，航迹长度为 110772.8158 米。最后讨 论了算法的有有效性和复杂性。 关于问题二，问题二是在问题一的基础上，由于相邻航段之间存在一定的夹角，且飞 行器受到结构和控制系统的限制，考虑飞行器的转弯半径的最小半径为 200m。因偏移角的 存在，飞行器航迹路径改变，不再沿上题规划的航径飞行，由 Dubins 最短路径理论可知， 此类路径是由圆弧段、直线段组成的。基于问题一建立的模型，重新描述主目标航迹段长 度的表达式，以校正条件和降落条件为约束，建立新的双目标航线规划模型。然后采用逐 步搜索的方法确定最优校正点，利用 MATLAB 软件对模型进行求解，得到的结果为：（1） 附件 1：航线经过的校正点与问题一相同，航迹长度为 106527.2290 米；（2）附件 2： 航 线经过的校正点与问题一相同，航迹长度为 111139.1823 米。最后与问题一的结果进行比 较分析，并且讨论了算法的有效性和复杂性。 关于问题三，问题三是在问题一的基础上，考虑校正失败的情形。部分校正点校正失败 的概率只有 20%，但为了保证飞行器成功完成任务，我们必须保证“零失败”，假定这些 校正点失败概率为 100%，在路径规划中，尽量避开这些校正点。基于问题一建立的模型， 改变校正点及 B 处的误差约束，建立新的双目标航线规划模型。对于问题一规划的两条优 化航迹路径，采用经典迭代方法进行一一检验，结果表明：（1）附件 1：两条航迹优化路 径 上 问 题 校 正 点 较 多 ， 且 不 能 满 足 约 束 条 件 ， 需 要 重 新 规 划 ， 新 的 规 划 航 迹 为 1
    A 503 294 91 607 61 278 369 214  555 B，经过 9 个校正点，航迹长度 为 105990.4001 米；（2）附件 2：问题一的两条优化路径也不满足约束条件，需重新规划。 但是，经过搜索，不存在这样符合条件的航线。因此，附件二中飞行器无法航行到 B 点。 此外，本文指出了其他针对航迹规划路径模型的算法，最后讨论了模型的优缺点并且 给出了模型的改进方向，以及模型的应用和推广。 关键词：最优化原理；经典迭代；双目标规划；最小转弯半径；剩余误差 2
    目录 一、问题重述................................................................................................................................. 4 1.1 问题描述........................................................................................................................... 4 1.2 问题提出........................................................................................................................... 4 二、 问题分析............................................................................................................................... 5 2.1 问题一的分析................................................................................................................... 5 2.2 问题二的分析................................................................................................................... 5 2.3 问题三的分析................................................................................................................... 5 三、 模型假设............................................................................................................................... 6 四、 符号说明............................................................................................................................... 6 五、模型的建立与求解................................................................................................................. 7 5.1 建模前的准备.................................................................................................................... 7 5.2 问题一的建模与求解........................................................................................................ 8 5.2.1 数据预处理............................................................................................................. 8 5.2.2 模型（航迹规划一般模型）的建立..................................................................... 8 5.2.3 模型（航迹规划一般模型）的求解................................................................... 10 5.2.4 结果与分析........................................................................................................... 12 5.2.5 算法有效性和复杂度的讨论............................................................................... 14 5.3 问题二的建模与求解...................................................................................................... 15 5.3.1 准备工作................................................................................................................ 15 5.3.2 模型（航迹规划一般模型）的建立................................................................... 15 5.3.3 模型（航迹规划一般模型）的求解................................................................... 19 5.3.4 结果与分析........................................................................................................... 21 5.3.5 算法有效性和复杂度的讨论............................................................................... 24 5.4 问题三的建模与求解...................................................................................................... 24 5.4.1 关于剩余误差 min（error，5）的理解.............................................................. 24 5.4.2 模型（航迹规划一般模型）的建立.................................................................... 24 5.4.3 模型（航迹规划一般模型）的求解.................................................................... 28 5.4.4 结果与分析............................................................................................................ 28 六、模型评价与改进................................................................................................................... 30 6.1 模型的评价...................................................................................................................... 30 6.1.1 模型的优点............................................................................................................ 30 6.1.2 模型的缺点............................................................................................................ 31 6.2 模型的改进...................................................................................................................... 31 七、 模型的应用和推广............................................................................................................. 31 八、参考文献............................................................................................................................... 31 附 录............................................................................................................................................. 32 1. 部分图（问题一次优路径航迹路径图）...................................................................... 32 2. 问题一附件 2 航迹路径规划表..................................................................................... 33 3. 部分 MATLAB 代码（详见附件终稿）........................................................................33 3
    一、问题重述 1.1 问题描述 复杂环境下航迹快速规划是智能飞行器控制的一个重要课题。由于系统结构限制，这 类飞行器的定位系统无法对自身进行精准定位，一旦定位误差积累到一定程度可能导致任 务失败。因此，在飞行过程中对定位误差进行校正是智能飞行器航迹规划中一项重要任务。 本文从优化“航迹长度尽可能小”和“经过校正区域进行校正的次数尽可能少”目标 出发，根据智能飞行器在飞行过程中的航迹长度引起的垂直误差和水平误差的多种航迹约 束条件下，搜索出满足校正条件的可校正点，从而解决系统定位精度限制下的航迹快速规 划问题，制定出相应的航迹规划路径。 其中，航迹约束条件如下： （1）飞行器在空间飞行过程中的定位误差包括垂直误差和水平误差。飞行器每飞行 1m， 垂直误差和水平误差将各增加个单位。到达终点时垂直误差和水平误差均应小于个单 位，并且当两个误差均小于个单位时，飞行器仍能够按照规划路径飞行。 （2）校正垂直和水平误差的位置形在航迹规划前确定。若在安全校正点处两个误差都能 得到及时校正，则飞行器最终可到达目的地。 （3）在出发地，飞行器的垂直和水平误差均为 0。 （4）飞行器在垂直误差校正点进行垂直误差校正后，其垂直误差将变为 0，水平误差不变。 （5）飞行器在水平误差校正点进行水平误差校正后，其水平误差将变为 0，垂直误差不变。 （6）当飞行器的垂直误差不大于 1 个单位，水平误差不大于 2 个单位时才能进行垂直误 差校正。 （7）当飞行器的垂直误差不大于 1个单位，水平误差不大于 2 个单位时才能进行水平误 差校正。 （8）飞行器在转弯时受到结构和控制系统的限制，无法完成即时转弯，假设飞行器的最 小转弯半径为 200m。 1.2 问题提出 问题一：本题考虑航迹约束条件（1）~（7）。建立满足两个目标及 7 个约束条件下 的智能飞行器建立从 A 点飞到 B 点的航迹规划一般模型和算法，讨论算法的有效性和复杂 度。绘出两个数据集的航迹规划路径，并将结果依次填入航迹规划结果表 问题二：本题考虑航迹约束条件（1）~（8）。在问题一的基础上考虑航迹约束条件 （8），即考虑飞行器转弯有最小转弯半径的情形，规划飞行器航迹。绘出两个数据集的 航迹规划路径，并将结果依次填入航迹规划结果表。 问题三：本题考虑航迹约束条件（1）~（7）。在问题一的基础上，由于飞行器因天 气等不可控因素导致其到达校正点无法进行理想校正，现假设飞行器在部分校正点（附件 1 和附件 2 中 F 列标记为“1”的数据）能够成功将某个误差校正为 0 的概率是 80%，如果 校正失败，则校正后的剩余误差为 min(error，5)个单位（其中 error 为校正前误差，min 为 取小函数），并且假设飞行器到达该校正点时即可知道在该点处是否能够校正成功，但不 论校正成功与否，均不能改变规划路径。重新规划飞行器航迹，并要求成功到达终点的概 率尽可能大。绘出两个数据集的航迹规划路径，并将结果依次填入航迹规划结果表。 4
    2.1 问题一的分析 二、问题分析 数据筛选 航迹一般 模型的建立 基于经典迭代 方法搜索校正点 结果与分析、算法 有效性和复杂性讨论 图 2-1 问题一思路框架图 问题一不考虑飞行器飞行时的转弯情况，只考虑航迹规划问题。要在尽可能短的航迹 长度基础上，最小化经过的校正点数目。这里我们假设飞行器在所有校正点处均可以成功 校正误差，不考虑天气及机体构造因素的影响。 针对此类问题，我们首先以校正点到出发点和目的地直线的距离为依据，对附件中的 校正点数据进行筛选，获得备选校正点库 1，然后以航迹长度最小化和校正点数目最小化 为目标，分首校正点为垂直校正点和水平校正点两种情况讨论，在校正点处校正条件、目 的地处降落条件为约束下，建立一个双目标的飞行器航迹规划模型，再利用经典迭代方法 逐个搜索最优校正点，在搜索过程中，我们建立了一个权重函数模型来帮助我们筛选，最 后根据得到的结果进行分析和评价，确定最优航迹路径，并且讨论了算法的有有效性和复 杂性。 2.2 问题二的分析 数据筛选 航迹一般 模型的建立 基于逐步搜索 方法确定校正点 结果与分析、算法 有效性和复杂性讨论 图 2-2 问题二思路框架图 问题二是在问题一的基础上，考虑加入飞行器飞行时的转弯情况。针对本题，因偏移 角的存在，飞行器飞行航迹路径改变，不再沿问题一规划的航径飞行，而由 Dubins 最短路 径理论可知，此类路径是由圆弧段、直线段组成的。基于问题一建立的模型，重新构造主 目标函数航迹段长度的函数，以校正条件和降落条件为约束，建立一个双目标航迹规划模 型，然后利用逐步搜索的方法确定最优校正点，最后得出最优航迹规划，与问题一的结果 比较分析，并且讨论了算法的有效性和复杂性。 2.3 问题三的分析 数据筛选 航迹一般 模型的建立 检验原航迹，不 满足，重新规划 结果与分析 图 2-3 问题三思路框架图 问题三是在问题一的基础上，考虑校正失败的情形。部分校正点校正失败的概率只有 20%，但为了保证飞行器成功完成任务，我们必须保证“零失败”，认定这些校正点失败 概率为 100%，在路径规划中，尽量避开这些校正点。针对本题，在问题一模型基础上， 考虑剩余误差约束条件，再加上原有约束条件，重新建立双目标航迹优化模型。对问题一 确定的两条优化路径，就附件中的标记问题点，代入模型中，检验是否满足约束条件，若 5
    满足，则无需重新规划，否则，按照模型，需要重新规划满足约束条件和主次目标的航迹， 并对其进行分析和说明。 三、模型假设 1、假设飞行器的飞行速度对于本文航迹规划问题没有影响。 2、假设飞行器在飞行过程中燃油供给十分充足。 3、忽略特殊因素，不考虑转弯情况，从一个点（出发点，校正点）到另一个点（校正点， 目的地）的飞行航迹是直线段。 4、校正点是有效的，且在安全区域，飞行器可到达任意一个校正点进行误差校正。 四、符号说明 符号含义 符号 L Ci il it +1Nt is +1Ns before iT i i 1 N  N ； Ci 到 +1Ci 的长度， =1,2,..., 刚到达第i 个校正点处未校正前的垂直误差， =1,2,..., 智能飞行器从出发点 A 到目的地 B 的航迹长度 第i 个校正点， =1,2,..., 为方便，约定以 0C 来标记出发点 A，以 1CN  来标记目的地B 到达目的地B 时的垂直误差 到达目的地B 时的水平误差 刚到达第i 个校正点处未校正前的水平误差， =1,2,..., N N i i 到达 +1Ci 时累积的垂直误差， =0,1,..., i N 到达 +1Ci 时累积的水平误差， =0,1,..., before iS ,  垂直误差校正点处的垂直误差和水平误差约束参数 N i 1 2 2 ,  水平误差校正点处的垂直误差和水平误差约束参数 1   r 到达目的地B 处的误差（包括垂直和水平误差）约束 飞行器每飞行 1m，垂直误差和水平误差增加的专用单位量 转弯半径， minr 为最小转弯半径 beforenew iT 考虑转弯半径时到达 +1Ci 时累积的垂直误差， =0,1,..., i N beforenew iS 考虑转弯半径时到达 +1Ci 时累积的水平误差， =0,1,..., i N 注：本文对小数较多的数据保留小数点后四位。 6
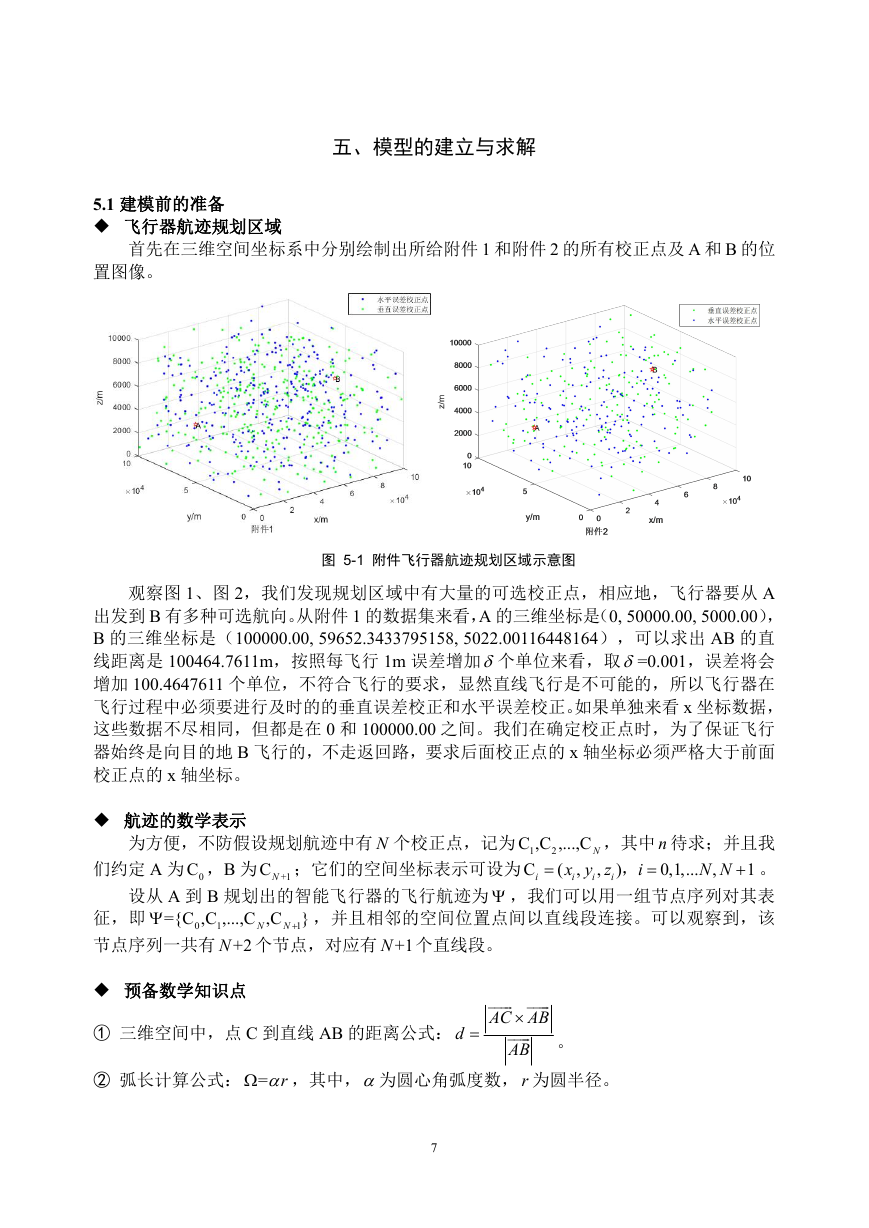
    五、模型的建立与求解 5.1 建模前的准备  飞行器航迹规划区域 首先在三维空间坐标系中分别绘制出所给附件 1 和附件 2 的所有校正点及 A 和 B 的位 置图像。 图 5-1 附件飞行器航迹规划区域示意图 观察图 1、图 2，我们发现规划区域中有大量的可选校正点，相应地，飞行器要从 A 出发到 B 有多种可选航向。从附件 1 的数据集来看，A 的三维坐标是（0, 50000.00, 5000.00）， B 的三维坐标是（100000.00, 59652.3433795158, 5022.00116448164），可以求出 AB 的直 线距离是 100464.7611m，按照每飞行 1m 误差增加个单位来看，取=0.001，误差将会 增加 100.4647611 个单位，不符合飞行的要求，显然直线飞行是不可能的，所以飞行器在 飞行过程中必须要进行及时的的垂直误差校正和水平误差校正。如果单独来看 x 坐标数据， 这些数据不尽相同，但都是在 0 和 100000.00 之间。我们在确定校正点时，为了保证飞行 器始终是向目的地 B 飞行的，不走返回路，要求后面校正点的 x 轴坐标必须严格大于前面 校正点的 x 轴坐标。  航迹的数学表示 们约定 A 为 0C ，B 为 +1CN ；它们的空间坐标表示可设为 C (  为方便，不防假设规划航迹中有 N 个校正点，记为 1 2C ,C ,...,C N ，其中 n 待求；并且我 。 设从 A 到 B 规划出的智能飞行器的飞行航迹为  ，我们可以用一组节点序列对其表 ，并且相邻的空间位置点间以直线段连接。可以观察到，该 , x y z i i 0,1,... N N , ) i ， 1  ={C ,C ,...,C ,C } 1 N  征，即 节点序列一共有 +2N 个节点，对应有 +1N 个直线段。 N 0 1  i , i   预备数学知识点 ① 三维空间中，点 C 到直线 AB 的距离公式： d    AC AB   。 AB ② 弧长计算公式： = r ，其中，为圆心角弧度数， r 为圆半径。 7
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料