第1页 / 共21页
第2页 / 共21页
第3页 / 共21页
第4页 / 共21页
第5页 / 共21页
第6页 / 共21页
第7页 / 共21页
第8页 / 共21页
随机前沿分析模型简明操作.pdf
¯c'.{†
by Timothy J.Coelli, et al
´R n
2017 c 3 21 F
1 ¡Œ¯)c.
1.1 (‰5)c
|^ŒO)cIJ…Œ/“5:§~^…Œ/“)
).d£C)D⁄)…ŒØŒ£Translog⁄)…Œ§Aigner and Chu
£1968⁄˜kƒ^ø«{O).d)…Œ" b‰¡Œ„N
ln qi = x
ߧ(‰5)c.–L«Xe
iβ − ui,
(1)
iL«d\ØŒ|⁄k × 1§ui·N
“¥§qiL«1iߧx
u)|"ˇqi–¯£=(
EˆK=§ˇ~bl'|N (0, σ2
‰5⁄exp(x
iβ) §⁄–(1) “L«·(‰5)c"·§øˆ{
¯D(Eˆ'lm5§
1 ¡Œ¯)c.
).d¯)c.L«Xe
ln qi = β0 + β1 ln xi + vi − ui
qi = exp(β0 + β1 ln xi + vi − ui)
× exp(vi)
qi = exp(β0 + β1 ln xi)
¯D(
(‰'
2
(3)
(4)
(5)
× exp(−ui)
ˆ5
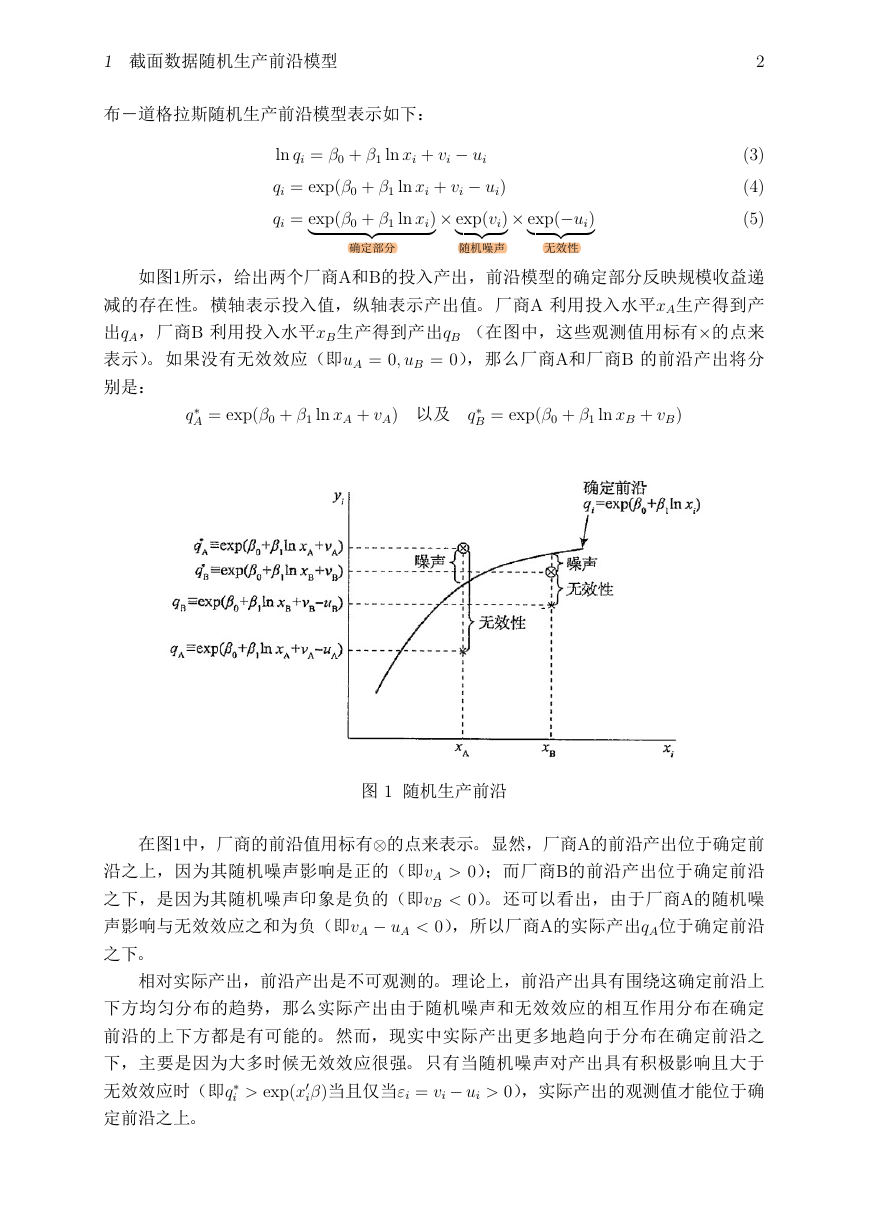
Xª1⁄«§ßAB\§c.(‰'N5´ˆ4
~35" ¶L«\§p¶L«" ßA |^\Y†xA)
qA§ßB |^\Y†xB)qB £3ª¥§ø*^Ik×:5
L«⁄" XJvkˆA£=uA = 0, uB = 0⁄§@oßAßB c'
O·
q∗
A = exp(β0 + β1 ln xA + vA) –9 q∗
B = exp(β0 + β1 ln xB + vB)
ª 1 ¯)c
3ª1¥§ßc^Ik⊗:5L«"w,§ßAcu(‰c
§ˇ¯D(K·£=vA > 0⁄¶ßBcu(‰c
e§·ˇ¯D(<·K£=vB < 0⁄" –w§dußA¯D
(KˆAK£=vA − uA < 0⁄§⁄–ßA¢SqAu(‰c
e"
Ø¢S§c·*"n§ck7ø(‰c
e!'“‡§@o¢Sdu¯D(ˆAp^'3(‰
ce·kU" ,§y¢¥¢Sı/“u'3(‰c
e§·ˇıˆAØr" k¯D(Øk¨4Ku
iβ)=εi = vi − ui > 0⁄§¢S*Uu(
ˆA£=q∗
‰c"
i > exp(x
1 ¡Œ¯)c.
3
¯c'83uˆA£–¡Eˆ˙§⁄" ~^
E˙u*¢SA¯c’
T Ei =
qi
exp(x
iβ + vi)
=
exp(x
iβ + vi)
exp(x
iβ + vi − ui)
= exp(−ui)
(6)
d(6)“⁄E˙1ißk߃^\⁄U
mا·[0,1]" w,§E˙T Ei§˜kI
O¯)c.(2)“¥ºŒ"
1.3 '¯)c.ºŒO
Aigner, Lovell and Schmidt£1977⁄’u.bXe
vi ∼ iidN (0, σ2
v)
ui ∼ iidN +(0, σ2
u)
(7)
(8)
b“(7)L†¯D(vi·Æ'¯C§0σ2
v"
b“(8)L†§ˆ˙ui ·Æ'¯C§¥”ºŒσ2
u§
·‘§zuiV˙…Œ£pdf⁄·0σ2
u V˙…Œ
/“" §—/?1ºŒO§Ø¯D(ˆ˙ªb§
‹bp’!pÆ"
3øbe§D˚ˇƒ{£OLS⁄ˆ{…XŒˆO§
—{·q,{£ML⁄5O."3¢S¥§ˇ~|^Frontier^
?1.ºŒO§8cT^#·4.1"Battese and Corra £1977⁄§
Frontier4.1Øø.ØŒq,…ŒUσ2 = σ2
u/σ2 ?1ºŒ
z"ºŒγ·[0,1]§XJγ = 0§K.3EˆA§⁄kØuc
l·d¯D("
uγ = σ2
v + σ2
1
2
3
...
58
59
60
1
1
1
...
1
1
1
L 1 Œ'EG1.dta
2.547725
3.189859
3.037594
...
3.061426
3.300419
2.646529
2.242410
1.535361
1.628260
...
2.233128
2.058473
1.726510
3.559169
4.347655
4.497574
...
4.467332
4.099995
3.789132
e¡–').d)c.~§øªXƒ^Frontier4.1^
?1.ºŒOE˙"duFrontier4.1 U?n5§§ˇdIØ
).d)…Œ>ØŒ§N.§Xe
ln(Qi) = β0 + β1 ln(Ki) + β2 ln(Li) + (vi − ui)
(9)
1 ¡Œ¯)c.
4
“¥§Qi! KiLi'O·! ]N˜§viui'Ol'" Œ
'eg1.dta¥„60ß1 c¡*§Uß?£firm-id⁄! ˇ?
£time-period⁄!ØŒ£ln Qi⁄!ØŒ]£ln Ki⁄ØŒN˜£ln Li⁄^S¯
¥y£L1⁄"
,ˇLFrontier4.1JłBlank.ins'M§S$1⁄I-'£ø
p•¶eg1.ins⁄§-'SN’)”L2" 11 1ƒ^rJ
..1·E.§)ßdu¯D(ˆA˛^„eE
˙flK¶.2·E˙K.§)ß¡Œ^eE˙=
ˇKflK¶w,§øp9ØE˙Kˇ'§ˇdJ.1"
121131ƒ^r‰Œ'¶¡'¶¡" nø¶¡·
–?¿•¶§·Frontier4.1ƒ¶¡7Lƒ^='£–V\Œi'º
˛⁄¤L§ƒ–Œ'¶¡'¶¡ØA"
141ƒ^rJ·)…Œ·⁄…Œ" ø~f˜·).d
)…Œ¯c.§ˇdJ1"
151˛fl^r·˜ØˇCØŒ" XJŒ'¥ˇCŒfi†LØ
Œ§Jy¶XJvkØŒ§Jn"3ø~f¥§•fi†ØˇCLØŒ
§ˇdJy"
161ƒ^rW˜¡Œ" øp§•„60ߧˇd¡
Œ60"
171ƒ^rW˜ˇŒ" du·¡Œ§ˇŒkc§ˇd
øpW1"
181ƒ^rW*Œ" Øu†¡Œ§øŒ·¡
ŒˇŒƒ¨¶Øu†¡Œ§I3ªƒ¨˜:~"
Œ¶Øu¡Œ§øŒ¡Œ"ˇd§3ø~f¥AW60"
191ƒ^rW.¥)”CŒ" •).d)…Œ¥
˜]N˜«\ØßK§ˇd)”CŒ2"
1101˛fl^r·˜ØMUD" XJ111J.1§øp·ØuD¶X
J111J.2§øp·Øδ0D" w,§3ø~f¥§AT·ØuD" d
§I.'/5߉·˜DXJb‰ui l'§AT
Jn¶XJb‰ui l'§ATJy"w,§ø~fATJn"
1111˛fl^r·˜ØETAD" Øu.1§ETANE˙·˜‹
mu)Cz"w,§Øu¡Œ§I˜mCzflK§ˇdøpAJn"
Øu.2§ETANKE˙ˇk=§dø17LWŒ£=K
ˇŒ⁄§1101’uMU£7Ly"
1121˛fl^r·˜‰—'" 3?„e§øp·n§ˇ•F
"Frontier4.1ˇL|¢5‰•—'§ø’^rˆ‰—'O(
ı"
1 ¡Œ¯)c.
5
1
1=Error Components Model, 2=TE Effects Model
J.
L 2 -'EG1.ins
EG1.dta Data File Name
EG1.out Output File Name
1=Production Function, 2=Cost Function
Logged Dependent Variable (y/n)
Number of Cross-sections
Number of Time Period
Number of Observations in Total
‰Œ'¶¡
‰'¶¡
)…Œ·⁄…Œ
ˇC·˜LØŒ
¡Œ
ˇŒ
*Œ
1
y
60
1
60
2
n
n
n
Number of Regressor Variables (Xs)
MU (y/n)[Or Delta0 (y/n) if Using TE Effects Model] ·˜u‰δ0D
ETA (y/n)[Or Number of TE Effects Regressors (Zs)] ·˜ηD‰WKˇŒ
)”CŒ
Starting Values (y/n)
·˜ˆ˜‰—'§Jn
,$1Frontier4.1^§.¡DOSI"øp‹˛fl^r·3“£=^
I¥⁄\-£\t⁄§·ˇL-'5$1§S£\f⁄" XJ\t§
@oI¥‹ƒ^r¯£f-'¥y⁄kflK¶XJ\f§KI
-'¶¡£„*—¶⁄\§,£$1"øw5§flk?6—-'
8·d?£flKL§§ˇdøp\f2\-'¶
“$1Frontier4.1" §S$1§‹y¶EG1.out'§.'(J
w«3ø'¥"
d uFrontier4.1 ' L § · n r 1 . ˚ ˇ ƒ O
£OLS⁄§dºŒ·ˆ¶1§^OLS O⁄ºŒ
—'?1|¢§,?\SzL§¶1n§SL§“§=
.ºŒq,O£MLE⁄"ˇd§'·Uøn‰w«(J§¿
‹3w«E˙O"L3!L4L5 'Ow«OLSO(J!†L
|¢O(J“q,O(J"
L 3 'EG1.out1'OLSO
the ols estimates are:
beta0
beta1
beta2
sigma-squared
coefficient
standard-error
t-ratio
0.24489834E+00
0.21360307E+00
0.11465114E+01
0.28049246E+00
0.53330637E+00
0.11398496E+00
0.48066617E-01
0.51498586E-01
0.58354940E+01
0.10355748E+02
log likelihood function = -0.18446849E+02
L3¥§beta0ØA.§beta1·]\£ln Ki⁄ºŒO§beta2·
N˜\£ln Li⁄ºŒO§sigma-squaredL«.¥d¯D(ˆA˛
^" l(J5w§]\N˜\5'O0.280.53§
¿31% w˝5Y†ˇLtu" ·§duO·k§ˇ
1 ¡Œ¯)c.
6
dOLSO(J¿vk¢S¿´§Ue|¢—'"
L 4 'EG1.out1'|¢O(J
the estimates after the grid search were:
beta0
beta1
beta2
sigma-squared
gamma
coefficient
0.58014216E+00
0.28049246E+00
0.53330637E+00
0.22067413E+00
0.80000000E+00
mu is restricted to be zero
eta is restricted to be zero
Øu|¢ºŒO'§•w“q,O
(J£MLE⁄§L5" –w§OLS O(J’§MLE O¿§
Ok5" Frontier4.1γ = σ2
u/σ2 ØŒq,…ŒºŒz§
Oγ = 0.7972§ø’p31%w˝5Y†ˇLtu§L†E
C·dˆ˙£u⁄"ºŒβ1 = 0.2811 β2 = 0.5365L«]N
˜'OU)”28.11% 53.65%§˜˛†L˘¿´§¿UˇL
Ou"
L 5 'EG1.out1n'q,O
the final mle estimates are:
beta0
beta1
beta2
sigma-squared
gamma
coefficient
standard-error
t-ratio
0.56161963E+00
0.20261668E+00
0.27718331E+01
0.28110205E+00
0.53647981E+00
0.11398496E+00
0.79720730E+00
0.47643365E-01
0.45251553E-01
0.63909106E-01
0.63909106E-01
0.59001301E+01
0.11855501E+02
0.33954545E+01
0.58436004E+01
mu is restricted to be zero
eta is restricted to be zero
log likelihood function = -0.17027229E+02
LR test of the one-sided error = 0.28392402E+01
with number of restrictions = 1
[note that this statistic has a mixed chi-square distribution]
Frontier4.1'¥E˙O"œ“(6)ØßE˙
‰´T Ei = exp(−ui)§d^z*ßE˙O§–
gEˆ˙§ui"L6¥c·Frontier4.1$1'¥60
ßE˙O§•øpOAßEˆ˙§§w«31
n¥",§˙–w⁄·¥⁄kß˙§–w⁄·3‰
ßc1iß˙ˇ"" n§˙–ˇLˆ˙§ui
1 ¡Œ¯)c.
7
§¿–˙«m" 3A˙^¥§Shazam–A
‰ßE˙9«m§Frontierˆ{«m"
L 6 'EG1.out1o'E˙OEˆ˙§
firm
eff.-est.
1
2
3
...
58
59
60
0.65068880E+00
0.82889151E+00
0.72642592E+00
...
0.66471456E+00
0.85670448E+00
0.70842786E+00
mean efficiency =
0.74056772E+00
u
0.42972378E+00
0.18766600E+00
0.31961877E+00
...
0.40839756E+00
0.15466225E+00
0.30033820E+00
1.4 '¯)c.ºŒO
'.·Øˆ˙bk⁄Cz§dui ∼ iidN +(µ, σ2
u)"
'’§'„eˆ˙20§·~Œ" øp§•
–ØŒ)c.~§ƒ^Frontier4.1^O'c."
.N/“Xe
ln(Qi) = β0+β1 ln(Ki)+β2 ln(Li)+β3 ln(Ki)2+β4 ln(Li)2+β5 ln(Ki) ln(Li)+(vi−ui) (10)
“¥§Qi!Ki!Livi„´.e‰§·ˆ˙uil
'" ~faq§øp•˜kŒ'eg2.dta£L7⁄" du
ØŒ)…Œ’).d)…ŒO\]N˜\†
p§ˇdŒ'¥IO\n"§•flkØ⁄kCØŒ"
L 7 Œ'EG2.dta
1
2
3
...
58
59
60
1
1
1
...
1
1
1
2.547725
3.189859
3.037594
...
3.061426
3.300419
2.646529
2.242410
1.535361
1.628260
...
2.233128
2.058473
1.726510
3.559169
4.347655
4.497574
...
4.467332
4.099995
3.789132
5.028404
2.357333
2.651230
...
4.986860
4.237312
2.980835
12.667690
7.981118
18.902110
6.675219
20.228170
...
7.323218
...
19.957060
9.976124
16.809960
8.439730
14.357520
6.541973
’ ~ f§ - ' I › # ‰ Œ ' ' ¶ ¡§ ' O
EG2.dtaEG2.out¶)”CŒ?U5§ˇO\]N˜\
1 ¡Œ¯)c.
8
†p¶’uMU DJy§ˇXc')”§XJ؈˙b
'y§'n" ƒ-–C§I˜m
CzK"
1
1=Error Components Model, 2=TE Effects Model
J.
L 8 -'EG2.ins
EG2.dta Data File Name
EG2.out Output File Name
1=Production Function, 2=Cost Function
Logged Dependent Variable (y/n)
Number of Cross-sections
Number of Time Period
Number of Observations in Total
‰Œ'¶¡
‰'¶¡
)…Œ·⁄…Œ
ˇC·˜LØŒ
¡Œ
ˇŒ
*Œ
1
y
60
1
60
5
y
n
n
Number of Regressor Variables (Xs)
MU (y/n)[Or Delta0 (y/n) if Using TE Effects Model] ·˜u‰δ0D
ETA (y/n)[Or Number of TE Effects Regressors (Zs)] ·˜ηD‰WKˇŒ
)”CŒ
Starting Values (y/n)
·˜ˆ˜‰—'§Jn
OLS:
beta0
beta1
beta2
beta3
beta4
beta5
sigma-squared
L 9 'EG2.outOLSMLEO(J
coefficient
standard-error
t-ratio
0.55625612E+00
0.36337949E+00
0.15307857E+01
0.37854314E+00
0.19384373E+00
0.19528263E+01
0.34779928E+00
0.21214558E+00
0.16394369E+01
-0.92959011E-01
0.30049984E-01
0.84811417E-02
0.11036711E+00
0.45170712E-01
0.34924524E-01
0.45231451E-01
-0.20579488E+01
0.86042644E+01
0.18750541E+00
log likelihood function = -0.15857202E+02
µ = σ2
u = 0 £\⁄LLF
MLE:
beta0
beta1
beta2
beta3
beta4
beta5
coefficient
standard-error
t-ratio
0.75634273E+00
0.31780239E+00
0.23799152E+01
0.38643648E+00
0.16320617E+00
0.23677810E+01
0.35175493E+00
0.17255941E+00
0.20384569E+01
-0.93929604E-01
0.30592987E-01
0.85664268E-02
0.41900823E-01
0.28655714E-01
0.37942019E-01
-0.22417126E+01
0.10676051E+01
0.22577678E+00
sigma-squared
0.45413086E+00
0.29132405E+00
0.15588513E+01
gamma
mu
0.89276949E+00
0.96460242E-01
0.92553105E+01
-0.12734743E+01
0.12297575E+01
-0.10355491E+01
eta is restricted to be zero
log likelihood function = -0.13910334E+02
ˆLLF
LR test of the one-sided error = 0.38937374E+01
with number of restrictions = 2
[note that this statistic has a mixed chi-square distribution]
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
