logo资料库

水箱水流量问题.docx

发布时间：2022-06-02 发布人：admin 分类：说明书 资料大小：0.03M 资料格式：docx 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    （一）问题的提出：
    水箱水流量问题 班级： 姓名： 学号： 1
    水箱的水流量问题 （一）问题的提出： 许多供水单位由于没有测量流入或流出水箱流量的设备，而只能测量水箱中 的水位。试着通过测得的某时刻水箱中水位的数据，估计在任意时刻（包括水泵 灌水时间）t 流出水箱的流量 f(t)。 假设： (1)影响水箱流量的唯一因素是该区域公众对水的普通需要。 (2)水泵的灌水速度为常数。 (3)从水箱中流出水的最大流速小于水泵的灌水速度。 (4)每天的用水量分布都是相似的。 (5)水箱的流水速度可用光滑曲线来近似。 (6)当水箱的水容量达到 514.8g 时，开始泵水；达到 677.6 时，便停止泵水。 给出下面原始数据表，其中长度单位为 E（1E=30.24cm）。水箱为圆柱体，其 直径为 57E。 时间/s 0 3316 6635 10619 13937 17921 21240 25223 28543 32284 35932 39332 39435 43318 水位 210 E 3175 3110 3054 2994 2947 2892 2850 2795 2752 2697 泵水 泵水 3550 3445 时间/s 46636 49953 53936 57254 60574 64554 68535 71854 75021 79254 82649 85968 89953 93270 水位 210 E 3350 3260 3167 3087 3012 2927 2842 2767 2697 泵水 泵水 3475 3397 3340 （二）关键字 水箱 ，水流量，水箱容积 ，时间。 （三）问题分析与建立模型 引入如下记号： V——水的容积； Vi——时刻 ti（h）水的容积（单位 G，1G=3.785L（升）； f（t）——时刻 ti 流出水箱的水的流速，它是时间的函数（G/h）； p——水泵的灌水速度（G/h）。 根据要求先将上表中的数据做变换，时间单位用小时（h），水位高转换成水 2
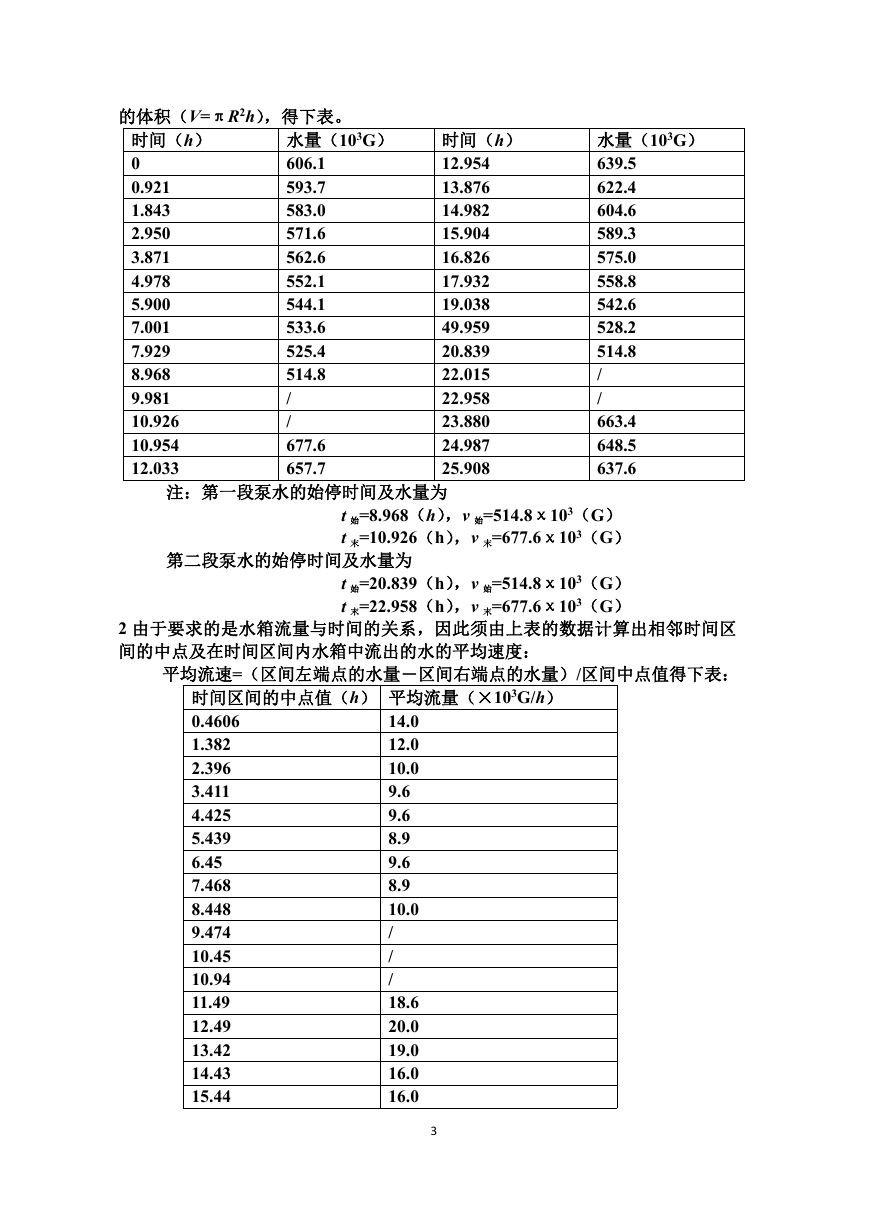
    的体积（V=πR2h），得下表。 时间（h） 0 0.921 1.843 2.950 3.871 4.978 5.900 7.001 7.929 8.968 9.981 10.926 10.954 12.033 水量（103G） 606.1 593.7 583.0 571.6 562.6 552.1 544.1 533.6 525.4 514.8 / / 677.6 657.7 时间（h） 12.954 13.876 14.982 15.904 16.826 17.932 19.038 49.959 20.839 22.015 22.958 23.880 24.987 25.908 水量（103G） 639.5 622.4 604.6 589.3 575.0 558.8 542.6 528.2 514.8 / / 663.4 648.5 637.6 注：第一段泵水的始停时间及水量为 t 始=8.968（h），v 始=514.8χ103（G） t 末=10.926（h），v 末=677.6χ103（G） 第二段泵水的始停时间及水量为 t 始=20.839（h），v 始=514.8χ103（G） t 末=22.958（h），v 末=677.6χ103（G） 2 由于要求的是水箱流量与时间的关系，因此须由上表的数据计算出相邻时间区 间的中点及在时间区间内水箱中流出的水的平均速度： 平均流速=（区间左端点的水量―区间右端点的水量）/区间中点值得下表： 时间区间的中点值（h） 平均流量（×103G/h） 0.4606 1.382 2.396 3.411 4.425 5.439 6.45 7.468 8.448 9.474 10.45 10.94 11.49 12.49 13.42 14.43 15.44 14.0 12.0 10.0 9.6 9.6 8.9 9.6 8.9 10.0 / / / 18.6 20.0 19.0 16.0 16.0 3
    16.37 17.38 18.49 19.50 20.40 21.43 22.49 23.42 24.43 25.45 做出散点图: 16.0 14.0 14.0 16.0 15.0 / / / 14.0 12.0 散点图 从图中可以看出数据分布不均匀，局部紧密，因此不能采用插值多项式处理 数据，而用曲线拟合的最小二乘法。 （四）计算过程 1． 算法： 第 1 步:输入数据{xi，yi}； 第 2 步:进行拟合； 第 3 步:作出散点图； 第 4 步:作出拟合函数图； 第 5 步:进行误差估算。 2． 实现: 在算法步 2 中使用 Fit[ ]函数，步 3、步 4 使用 Plot[ ]，步 5 选用 Integrate[ ] 函数。 3． 误差估计： 误差估算时，由于水泵的灌水速度为一常数，水箱中水的体积的平均变化速 V  t  应近似等于水泵的灌水速度 P 减去此段时间从水箱中流出的平均速度。即 度 P  V / t   dt f )( t t  此处 f（t）在Δt 区间的两端点间进行积分。 如果此模型确实准确地模拟了这些数据，那么在不同的灌水周期中，按此模 4
    型计算出的水泵灌水速度应近似为常数。下面通过水泵开始和停止工作的两段区 间，即 t∈[8.968，10.926] 及 t∈[20.839，22.958]来进行检验。 第一段： 对应于 t 始=8.968（h）， t 末=10.926（h） 水量分别为 v 始=514800（G），v 末=677600（G） 故 ΔV1=677600-514800=162800（G） Δt1=10.926-8.986=1.958（h） V  =83150（G/h） 1 t  1 t 始=20.839（h）， t 末=22.958（h） v 始=514800（G）， v 末=677600（G） 第二段： 对应于 水量分别为 所以 ΔV2=677600-514800=162800（G） Δt2=22.958-20.839=2.119（h） V  2 t  =76830（G/h） 2 1  t 1 926.10 968.8 1  t 2 958.22 839.20 f )( t dt f )( t dt P1=83150+ P2=76830+  PP  1 2 P 2 （五）结果分析 通过水泵开始和停止工作的两段时间检验水泵灌水速度应近似为常数；其中 由{1，x，x2，x3，…，x8}拟合的函数 f（t）所产生的误差为 8.217%，由{1，x3， x5，sin(0.1x)，cos(0.1x)}拟合达到 8.224%。由此可见如选择不同的基函数，将得 不同的误差。但是只要基函数选择恰当，所产生的误差也可以保持为相对稳定最 小常数来支持该模型。 同时，一旦确定了最佳 f（t），我们便可通过 Integrate[ ]函数估算出一天的用 水总量，从而根据常规每 1000 人用水量来推测出该地区的人口数，另外，还可求 得水箱的平均流速。 5
    6
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料