2004年吉林省吉林市中考数学真题及答案.doc-资料库

第1页 / 共13页

第2页 / 共13页

第3页 / 共13页

第4页 / 共13页

第5页 / 共13页

第6页 / 共13页

第7页 / 共13页

第8页 / 共13页

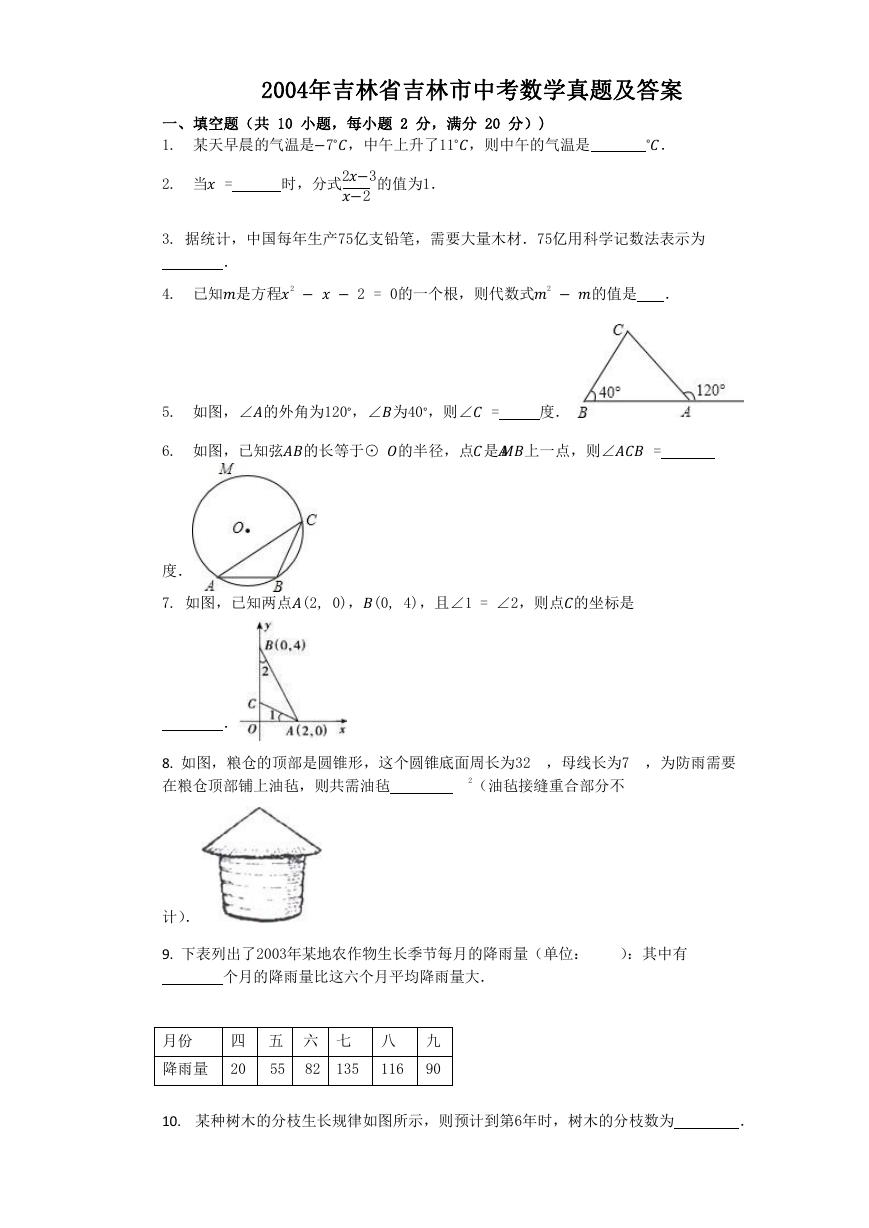
2004年吉林省吉林市中考数学真题及答案 ∘． 3. 据统计，中国每年生产75亿支铅笔，需要大量木材．75亿用科学记数法表示为．时，分式的值为1． 2−3 −2 一、填空题（共 10 小题，每小题 2 分，满分 20 分）) 1. 某天早晨的气温是−7∘，中午上升了11∘，则中午的气温是 2. 当 = 4. 已知是方程2 −− 2 = 0的一个根，则代数式2−的值是． 5. 如图，∠的外角为120∘，∠为40∘，则∠ = 6. 如图，已知弦的长等于⊙的半径，点是上一点，则∠ = 度．度． 7. 如图，已知两点(2, 0)，(0, 4)，且∠1 = ∠2，则点的坐标是． 8. 如图，粮仓的顶部是圆锥形，这个圆锥底面周长为32 ，母线长为7 ，为防雨需要在粮仓顶部铺上油毡，则共需油毡 2（油毡接缝重合部分不计）． 9. 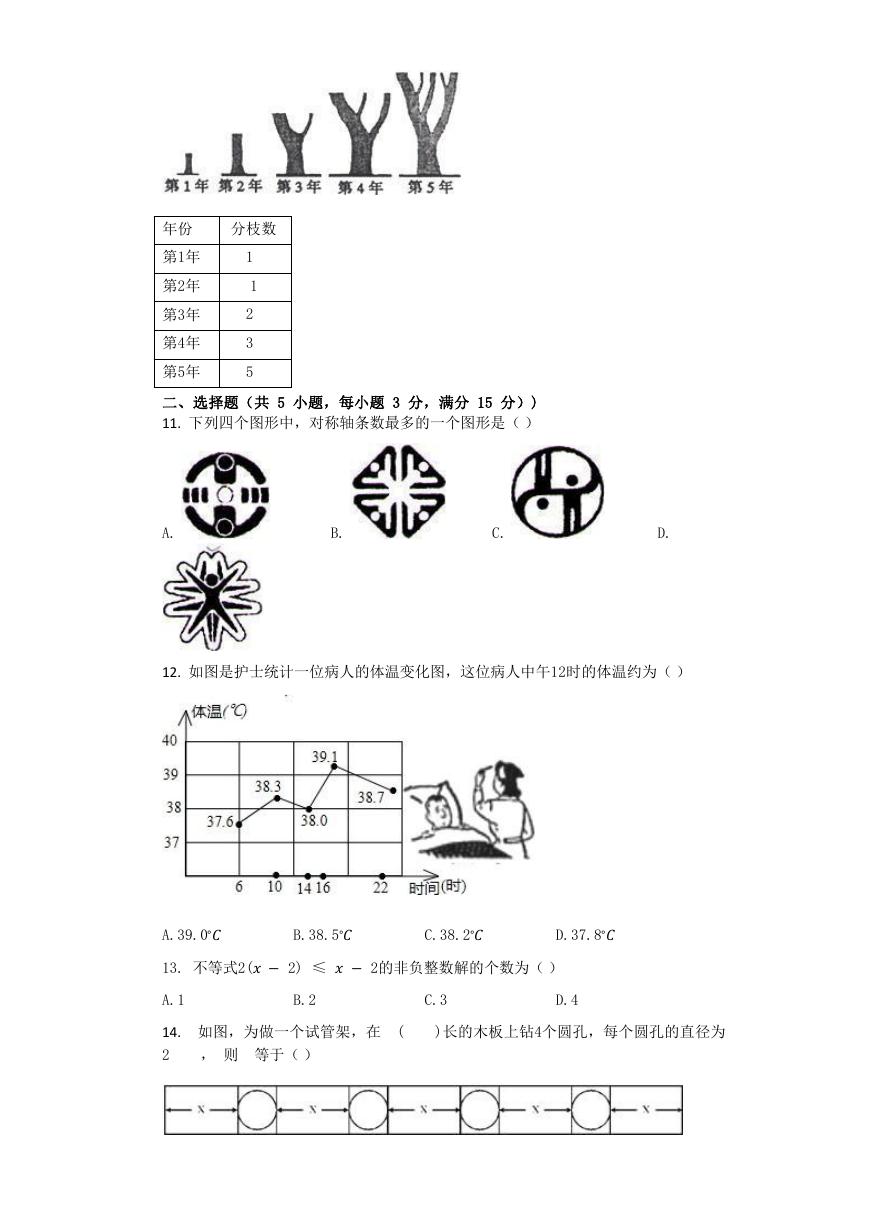下表列出了2003年某地农作物生长季节每月的降雨量（单位：）：其中有个月的降雨量比这六个月平均降雨量大．月份四五六七八九降雨量 20 55 82 135 116 90 10. 某种树木的分枝生长规律如图所示，则预计到第6年时，树木的分枝数为．

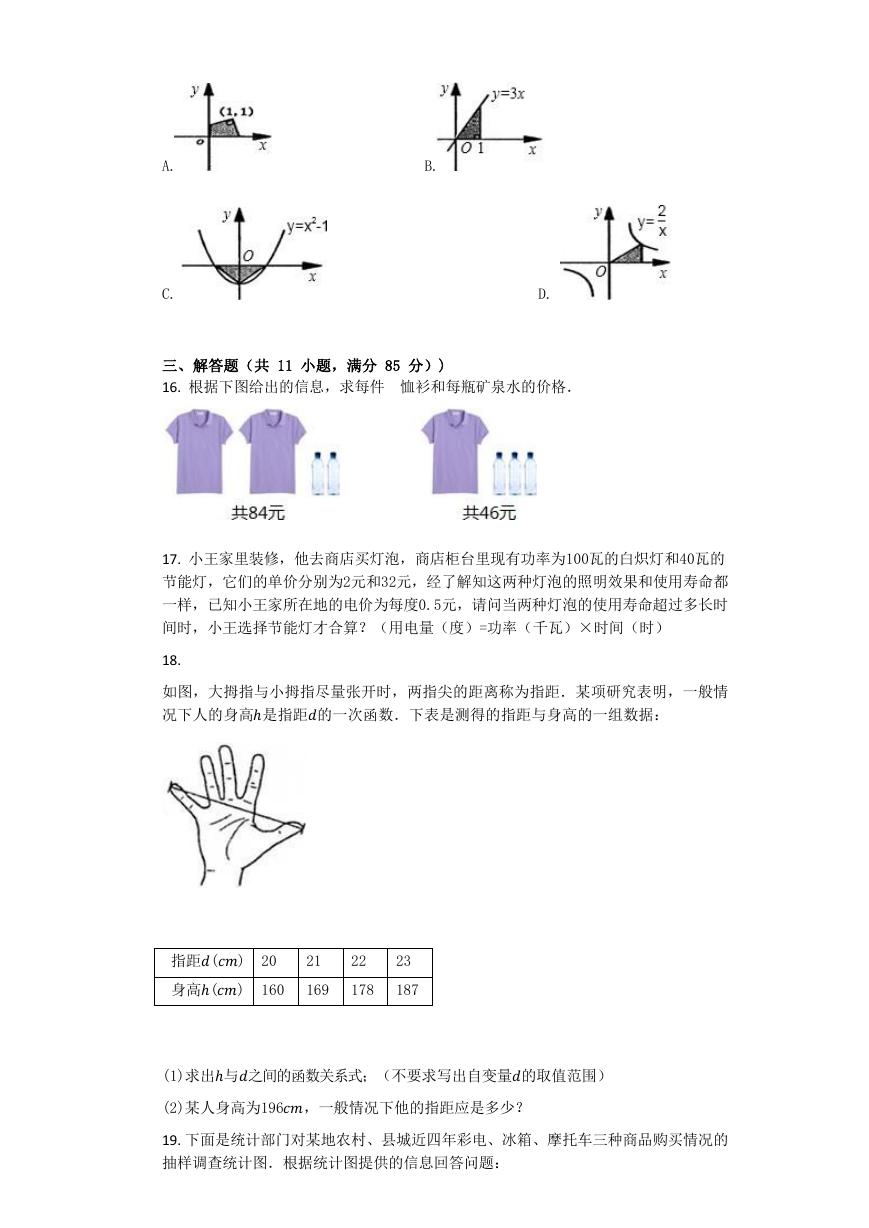
年份分枝数第1年第2年第3年第4年第5年 1 1 2 3 5 二、选择题（共 5 小题，每小题 3 分，满分 15 分）) 11. 下列四个图形中，对称轴条数最多的一个图形是（） A. B. C. D. 12. 如图是护士统计一位病人的体温变化图，这位病人中午12时的体温约为（） A.39.0∘ 13. 不等式2(− 2) ≤ − 2的非负整数解的个数为（） C.38.2∘ A.1 B.38.5∘ B.2 D.37.8∘ D.4 C.3 14. 如图，为做一个试管架，在 ( 2 ，则等于（） )长的木板上钻4个圆孔，每个圆孔的直径为

−4 5 C. 3 4 | + ( ) 1 2 2 −8 5 D. + 2−1的结果相同的是（） 15. 下列图中阴影部分面积与算式| A. −1 6 5 B. 5 +8 −

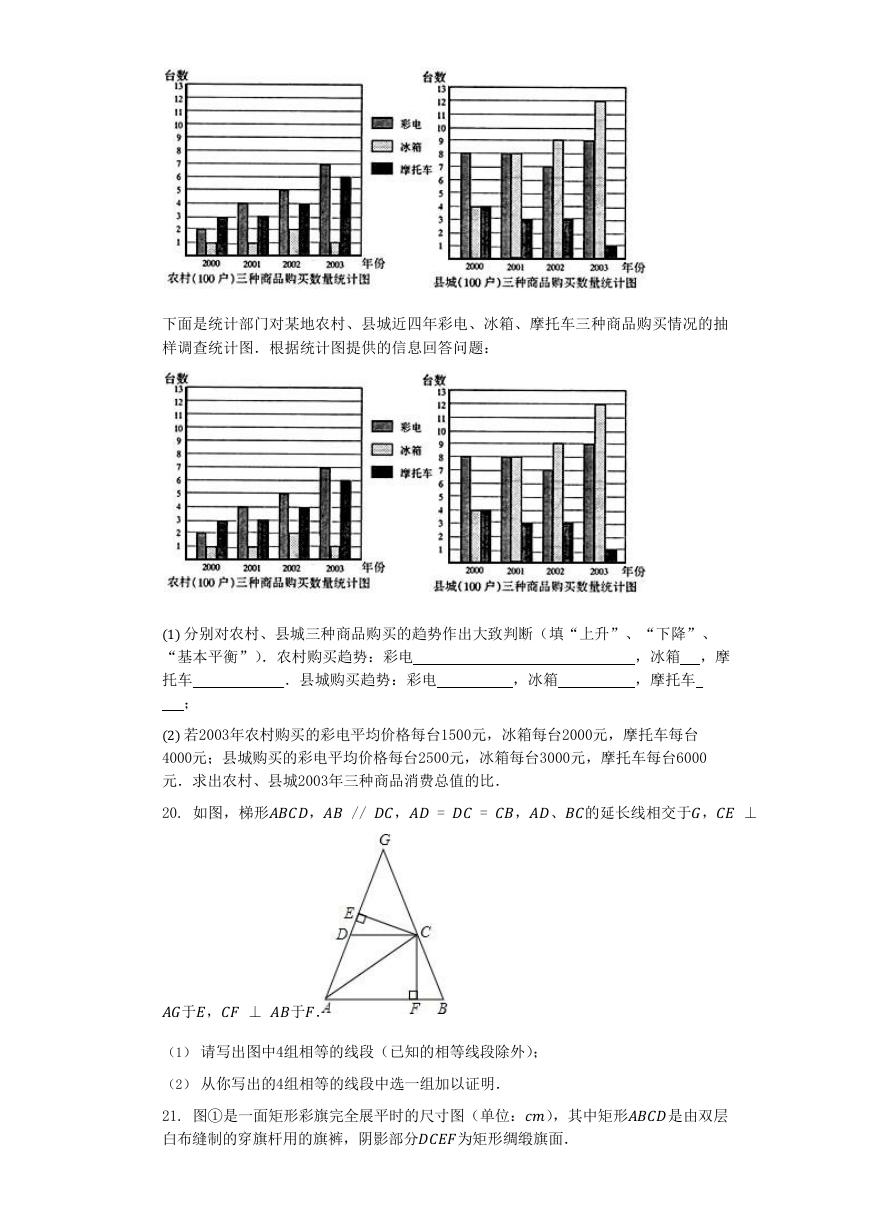
A. C. B. D. 三、解答题（共 11 小题，满分 85 分）) 16. 根据下图给出的信息，求每件恤衫和每瓶矿泉水的价格． 17. 小王家里装修，他去商店买灯泡，商店柜台里现有功率为100瓦的白炽灯和40瓦的节能灯，它们的单价分别为2元和32元，经了解知这两种灯泡的照明效果和使用寿命都一样，已知小王家所在地的电价为每度0.5元，请问当两种灯泡的使用寿命超过多长时间时，小王选择节能灯才合算？（用电量（度）=功率（千瓦）×时间（时） 18. 如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．某项研究表明，一般情况下人的身高ℎ是指距的一次函数．下表是测得的指距与身高的一组数据： 22 23 160 169 178 187 指距() 身高ℎ() (1)求出ℎ与之间的函数关系式；（不要求写出自变量的取值范围） (2)某人身高为196，一般情况下他的指距应是多少？ 20 21 19. 下面是统计部门对某地农村、县城近四年彩电、冰箱、摩托车三种商品购买情况的抽样调查统计图．根据统计图提供的信息回答问题：

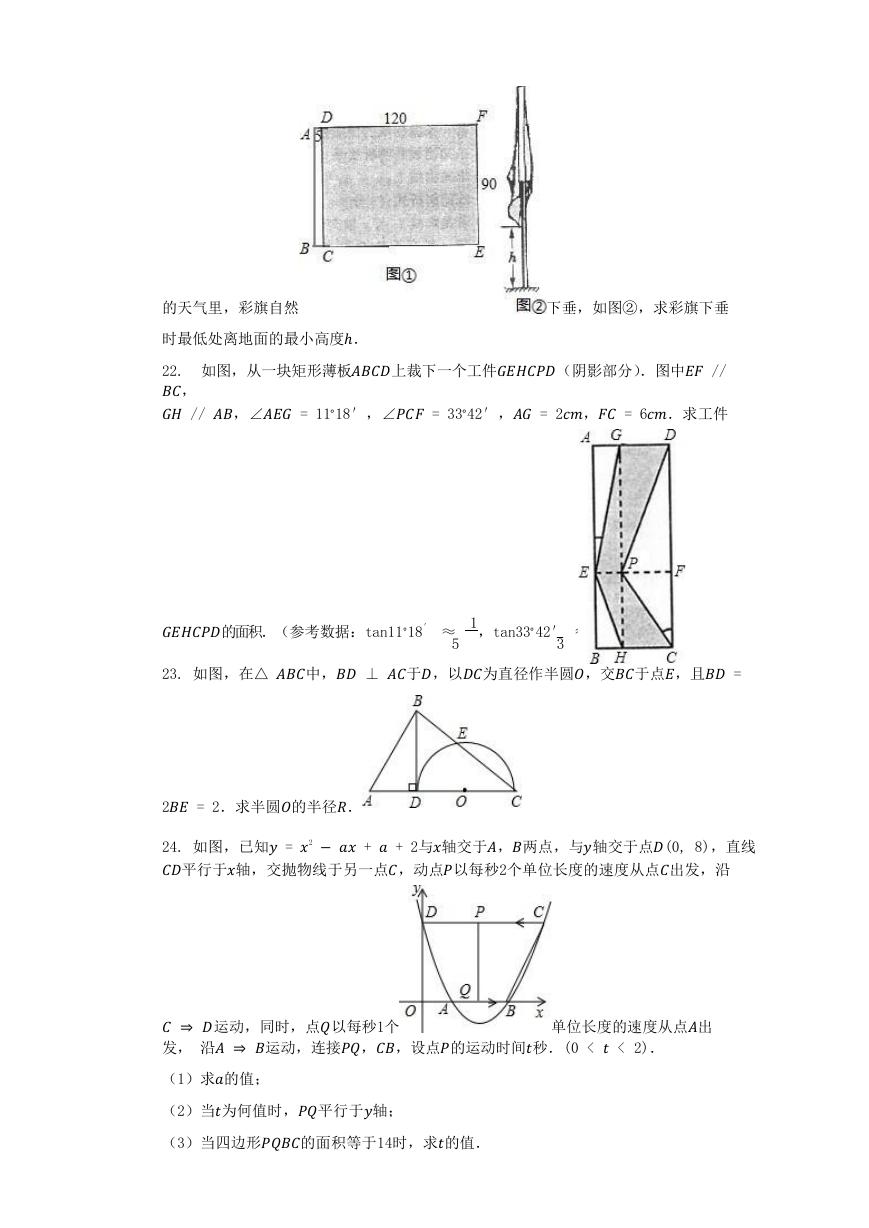
下面是统计部门对某地农村、县城近四年彩电、冰箱、摩托车三种商品购买情况的抽样调查统计图．根据统计图提供的信息回答问题：托车．县城购买趋势：彩电，冰箱，摩托车 “基本平衡”）．农村购买趋势：彩电 (1) 分别对农村、县城三种商品购买的趋势作出大致判断（填“上升”、“下降”、；(2) 若2003年农村购买的彩电平均价格每台1500元，冰箱每台2000元，摩托车每台 20. 如图，梯形， //， = =，、的延长线相交于， ⊥ 4000元；县城购买的彩电平均价格每台2500元，冰箱每台3000元，摩托车每台6000 元．求出农村、县城2003年三种商品消费总值的比．，冰箱，摩（1）请写出图中4组相等的线段（已知的相等线段除外）；于， ⊥于． 21. 图①是一面矩形彩旗完全展平时的尺寸图（单位：），其中矩形是由双层白布缝制的穿旗杆用的旗裤，阴影部分为矩形绸缎旗面．（2）从你写出的4组相等的线段中选一组加以证明．

（1）用经加工的圆木杆穿入旗裤作旗杆，求旗杆的最大直径（精确到1 ）；（2）将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为220 ，在无风

的天气里，彩旗自然下垂，如图②，求彩旗下垂时最低处离地面的最小高度ℎ． 22. 如图，从一块矩形薄板上裁下一个工件（阴影部分）．图中 // ， //，∠ = 11∘18′，∠ = 33∘42′， = 2， = 6．求工件的面积．（参考数据：tan11∘18′ ≈ 23. 如图，在△中， ⊥于，以为直径作半圆，交于点，且 = ，tan33∘42′ ≈ ） 2 1 5 3 2 = 2．求半圆的半径． 24. 如图，已知 =2− + + 2与轴交于，两点，与轴交于点(0, 8)，直线平行于轴，交抛物线于另一点，动点以每秒2个单位长度的速度从点出发，沿 ⇒ 运动，同时，点以每秒1个发，沿⇒ 运动，连接，，设点的运动时间秒．(0 < < 2)．（1）求的值；（2）当为何值时，平行于轴；（3）当四边形的面积等于14时，求的值．单位长度的速度从点出

25. 如图，正方形的边长为12，划分成12 × 12个小正方形格．将边长为(为整数，且2 ≤ ≤ 11)的黑白两色正方形纸片按图中的方式黑白相间地摆放，第一张 × 的纸片正好盖住正方形左上角的 ×个小正方形格，第二张纸片盖住第一张纸片的部分恰好为(− 1) × (− 1) 下去，最后直到纸片盖住正方形的右下角为止．请你认真观察思考后回答下列问题：的正方形．如此摆放（1）由于正方形纸片边长的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：纸片的边长使用的纸片张数 2 3 4 5 6 （2）设正方形被纸片盖住的面积（重合部分只计一次）为 1，未被盖住的面积为 2． ①当 = 2时，求1:2的值； ②是否存在使得1 =2的值，若存在，请求出这样的值；若不存在，请说明理由． 26. 已知抛物线: = 2 + +（其中、、都不等于0），它的顶点的坐标是 (− ， )，与轴的交点是(0,)．我们称以为顶点，对称轴是轴且过点的 2 抛物线为抛物线的伴随抛物线，直线为的伴随直线．已知抛物线: = 2 + +（其中、、都不等于0），它的顶点的坐标是 (− ， )，与轴的交点是(0,)．我们称以为顶点，对称轴是轴且过点的 4−2 4 4−2 抛物线为抛物线的伴随抛物线，直线为的伴随直线． 2 4 (1)请直接写出抛物线 = 2 2 − 4 + 1的伴随抛物线和伴随直线的解析式：伴随抛物线的解析式，伴随直线的解析式； (2)若一条抛物线的伴随抛物线和伴随直线分别是 = − 2 − 3和 = − − 3，则这条抛物线的解析式是； (3)求抛物线 : = 2 + + （其中、、都不等于0）的伴随抛物线和伴随直线的解析式； (4)若抛物线与轴交于 ( 1, 0)、 ( 抛物线与轴交于、两点，且 = 1 > 0，它的伴随 2, 0)两点， 2 > ．请求出、、应满足的条件．

资料库

2004年吉林省吉林市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料