2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc-资料库

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc.pdf-第1页.jpg

第1页 / 共6页

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc.pdf-第2页.jpg

第2页 / 共6页

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc.pdf-第3页.jpg

第3页 / 共6页

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc.pdf-第4页.jpg

第4页 / 共6页

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc.pdf-第5页.jpg

第5页 / 共6页

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc.pdf-第6页.jpg

第6页 / 共6页

2020-2021 学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案本试卷分卷 I 和卷 II 两部分；卷 I 为选择题，卷 II 为非选择题。本试卷总分 100 分，考试时间 100 分钟。试题答案写在答题卡上。卷 I 一、选择题（本大题共 12 个小题，每小题各 3 分，共 36 分。在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡上正确填涂。） 1．下列调查中，调查方式选择合理的是（） A．节能灯厂要检测一批节能灯的使用寿命，采用全面调查方式 B．调查某一品牌 5 万袋包装鲜奶是否符合卫生标准，采用抽样调查方式 C．了解秦皇岛市城区居民日平均用水量，采用全面调查方式 D．旅客上飞机前的安检，采用抽样调查方式 2．今年我县有 3900 名考生参加中考，为了了解这些考生的数学成绩，从中抽取 200 名考生的数学成绩进行统计分析，在这个问题中，下列说法正确的是（）： A．3900 名考生的中考成绩的全体是总体 B．每个考生是个体 C．200 名考生是总体的一个样本 D．样本的容量是 200 3．下列数据能确定物体具体位置的是（） A．东经 118°，北纬 28°B．希望路右边 C．北偏东 30°D．明华小区 4 号楼 4．点 P(2，－5)所在的象限是（） A．第一象限 B．第二象限 C．第三象限 D．第四象限 5．甲以每小时 20km 的速度行驶时，他所走过的路程 S(km)与时间 t（h）之间可用公式 s＝20t 来表示，则下列说法正确的是（） A．数 20 和 s，t 都是变量 B．s 是常量，数 20 和 t 是变量 C．数 20 是常量，s 和 t 是变量 D．t 是常量，数 20 和 s 是变量 6．在方格纸上画出的小旗图案如图所示，若用(﹣2，1)表示 A 点，(﹣2，5)表示 B 点，那么 C 点的位置可表示为（） A．(3，5)B．(1，3)C．(1，2)D．(5，3) 7．函数 y  1  1 x 自变量的取值范围是（）． A． 1x 8．在平面直角坐标系中，将三角形三个顶点的横坐标都增加 3，纵坐标保持不变，所得的新图形与原图形 B． 1x  C． 1x  D． x   1 相比（） A．向上平移了 3 个单位长度 C．向左平移了 3 个单位长度 B．向下平移了 3 个单位长度 D．向右平移了 3 个单位长度 9．过 A(4，－3)和 B(－4，－3)两点的直线一定( ) A．垂直于 x 轴 B．与 x 轴相交但不垂直 C．平行于 x 轴 D．平行于 y 轴 10．据不完全统计，2020 年 1--4 月份我国某型号新能源客车的月销量情况如图所示，下列说法错误的是（） A．1 月份销量为 2 万辆 B．从 2 月到 3 月的月销量增长最快

4, 2  C．4 月份销量比 3 月份增加了 0.9 万辆 D．1~4 月新能源客车销量逐月增加 11．已知点 P 在第四象限，且到 x 轴的距离为 2，到 y 轴距离是 4，则点 P 的坐标为（ A． 12．如图，动点 P 在平面直角坐标系中按图中箭头所示方向运动，第 1 次从原点运动到点(1,1)，第 2 次接着运动到点（2,0），第 3 次接着运动到点（3,2），…，按这样的运动规律，经过第 2021 次运动后，动点 P 的坐标是（ 4,2 2,4 C． B． ）） D． 2, 4  A．（2020， 0） B．（2021，1） C．（2021，2） D．（2021，0）二、填空题（本大题共 6 个小题，每题 2 分，共 12 分）卷Ⅱ（非选择题，共 64 分） 13．若电影票上座位是 12 排 5 号可记为（12，5），则（5，6）表示_______________ 14．点（-1， 2）关于 x 轴的对称点坐标是 15．在函数 1  中，自变量 x 的取值范围是 x y 16．为了了解某地区 45000 名九年级学生的睡眠情况，运用所学统计知识解决上述问题所要经历的几个主要步骤：①抽样调查；②设计调查问卷；③用样本估计总体；④分析、整理数据；按操作的先后进行排序为．（只写序号） 17．小明早上步行去车站，然后坐车去学校．如图象中，能近似的刻画小明离学校的距离随时间变化关系的图象是_____．（填序号） 18．根据如图所示的程序计算函数 y 的值，若输入 x 的值是 7，则输出 y 的值是三、解答题（本大题共 6 个小题；共 52 分。解答应写出演算步骤、证明过程或文字说明） 19．（6 分）如图，这是某市部分简图，请以火车站为坐标原点向东的方向为 x 轴的正方向，建立平面直角坐标系，并分别写出火车站以北（包括火车站）各地点的坐标（每个正方形边长是 1）

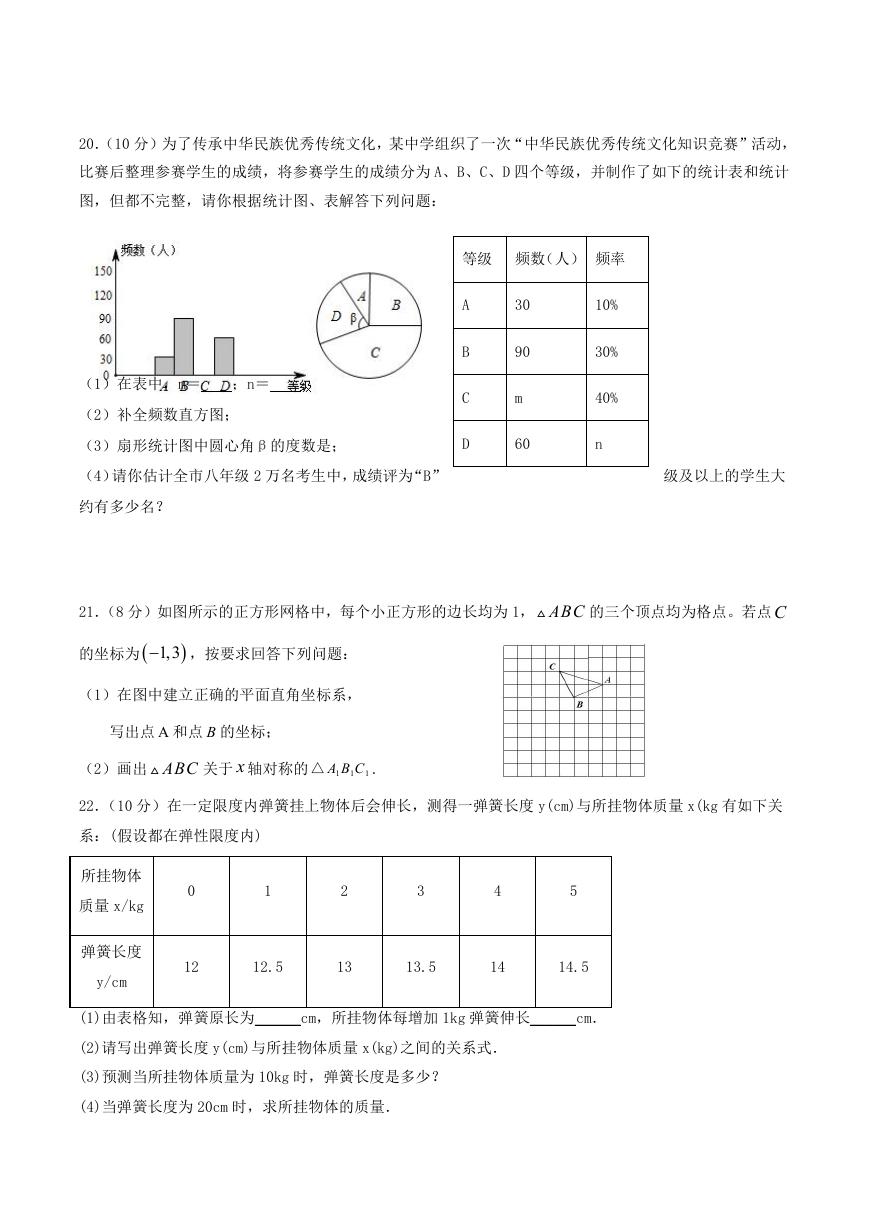
20．（10 分）为了传承中华民族优秀传统文化，某中学组织了一次“中华民族优秀传统文化知识竞赛”活动，比赛后整理参赛学生的成绩，将参赛学生的成绩分为 A、B、C、D 四个等级，并制作了如下的统计表和统计图，但都不完整，请你根据统计图、表解答下列问题：（1）在表中，m＝；n＝；（2）补全频数直方图；（3）扇形统计图中圆心角β的度数是；等级频数（人）频率 A B C D 30 90 m 60 10% 30% 40% n （4）请你估计全市八年级 2 万名考生中，成绩评为“B” 级及以上的学生大约有多少名？ 21．（8 分）如图所示的正方形网格中，每个小正方形的边长均为 1， ABC 的坐标为 ，按要求回答下列问题： 1,3  的三个顶点均为格点。若点C （1）在图中建立正确的平面直角坐标系，写出点 A 和点 B 的坐标；（2）画出 ABC  关于 x 轴对称的 1 △ A B C 1 . 1 22．（10 分）在一定限度内弹簧挂上物体后会伸长，测得一弹簧长度 y(cm)与所挂物体质量 x(kg 有如下关系：(假设都在弹性限度内) 所挂物体质量 x/kg 弹簧长度 y/cm 0 1 2 3 4 5 12 12.5 13 13.5 14 14.5 (1)由表格知，弹簧原长为______cm，所挂物体每增加 1kg 弹簧伸长______cm． (2)请写出弹簧长度 y(cm)与所挂物体质量 x(kg)之间的关系式． (3)预测当所挂物体质量为 10kg 时，弹簧长度是多少？ (4)当弹簧长度为 20cm 时，求所挂物体的质量．

23．（8 分）如图，已知长方形 ABCO 中，边 AB=12，BC=8．以点 0 为原点，OA、OC 所在的直线为 y 轴和 x 轴建立直角坐标系．（1）点 A 的坐标为（0，8），写出 B．C 两点的坐标；（2）若点 P 从 C 点出发，以 3 单位/秒的速度向 CO 方向移动（不超过点 O），点 Q 从原点 O 出发，以 2 单位/秒的速度向 OA 方向移动（不超过点 A），设 P、Q 两点同时出发，t 秒后，写出△BCP 的面积 S 与 t 之间的函数关系式；（3）在 P、Q 移动过程中，四边形 OPBQ 的面积是否发生变化?若不变，求其值；若变化，求变化范围． 24．（10 分）“龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD 和折线OABC 表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．（1）线段OD 表示赛跑过程中___________的路程与时间的关系（填“乌龟”和“兔子”）．赛跑的全程是_______米．（2）兔子在起初每分钟跑_____米，乌龟每分钟爬_____米．（3）兔子醒来，以 750 米/分的速度跑向终点，结果还是比乌龟晚到了 1 分钟，请你算算兔子中间停下睡觉用了多少分钟？一、选择题（本大题共 12 个小题，每小题各 3 分，共 36 分。在每小题给出的四个选项中，只有一项是符八年级数学答案合题目要求的，请在答题卡上正确填涂。） 1---6 B D A D C B 7---12 C D C D A B 二、填空题（本大题共 6 个小题，每题 2 分，共 12 分） 13．5 排 6 号 14. （-1，-2） 15. x≥1 16. ②①④③ 17. ④ 18. -1 三、解答题（本大题共 6 个小题；共 52 分。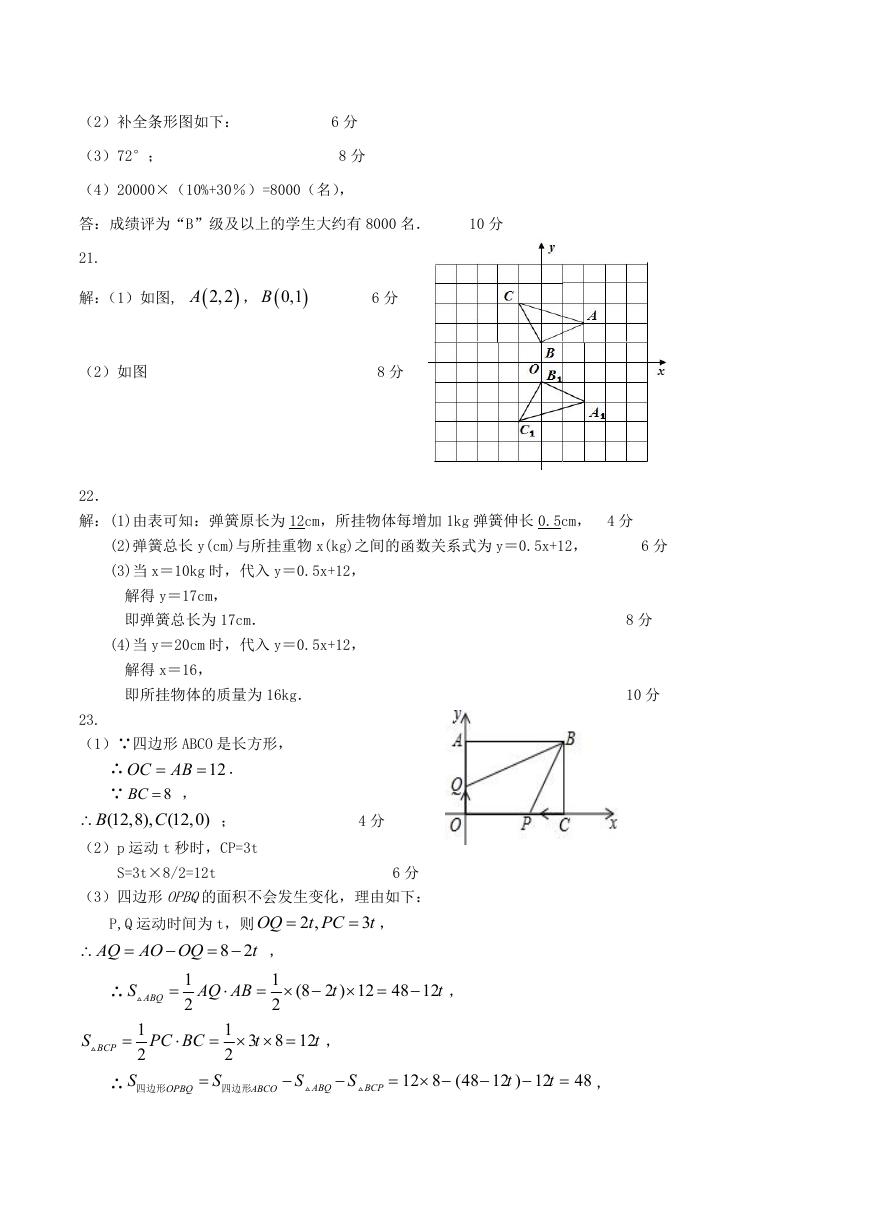解答应写出演算步骤、证明过程或文字说明） 19．解：以火车站为坐标原点向东的方向为 x 轴的正方向，建立平面直角坐标系如图所示 1 分由坐标系可知：火车站（0,0），文化宫（-3,1），体育场（-4,3），宾馆（2,2），市场（4,3）． 5 分 20. 解：（1）m＝120，n＝20%， 4 分

（2）补全条形图如下：（3）72°； 6 分 8 分（4）20000×（10%+30％）=8000（名），答：成绩评为“B”级及以上的学生大约有 8000 名． 10 分 21. 解：（1）如图, A  2,2 ，  B 0,1 （2）如图 22． 6 分 8 分解：(1)由表可知：弹簧原长为 12cm，所挂物体每增加 1kg 弹簧伸长 0.5cm， 4 分 (2)弹簧总长 y(cm)与所挂重物 x(kg)之间的函数关系式为 y＝0.5x+12， 6 分 (3)当 x＝10kg 时，代入 y＝0.5x+12，解得 y＝17cm，即弹簧总长为 17cm． (4)当 y＝20cm 时，代入 y＝0.5x+12，解得 x＝16，即所挂物体的质量为 16kg． 23. （1）∵四边形 ABCO 是长方形，  ． 12 ∴ OC AB BC  ， 8 (12,0) C ∵ (12,8), ； 4 分  B （2）p 运动 t 秒时，CP=3t S=3t×8/2=12t 6 分（3）四边形 OPBQ的面积不会发生变化，理由如下： OQ P,Q 运动时间为 t，则 8 2 t   ，   2 , t PC  ， 3 t   AQ AO OQ 1 2 ABQ ∴  S  S  BCP  1 2 PC BC  1 (8 2 ) 12    2  t  48 12 t  ，  AQ AB 1 3 t     2 8 12 t ， ∴ S 四边形 OPBQ  S 四边形 ABCO  S  ABQ  S  BCP  12 8 (48 12 ) 12 t     t 8 分 10 分  48 ，

∴四边形 OPBQ的面积不会发生变化，其值始终为 48． 8 分 24. 解：（1）乌龟、1500；（2）600、50； 4 分 8 分（3）兔子全程共用 31 分钟，其中，开始跑了 1 分钟，后来又跑了（1500-600）÷750=1.2 分钟 31−1−1.2＝28.8（分钟）， ∴兔子中间停下睡觉用了 28.8 分钟． 10 分说明：以上答案和评分标准作为参考，如有不同做法，酌情给分

资料库

2020-2021学年河北省秦皇岛市青龙县八年级下学期期中数学试题及答案.doc

相关推荐

初中二年级

热门标签

最新资料