2023年山西长治中考数学真题及答案.doc-资料库

第1页 / 共13页

第2页 / 共13页

第3页 / 共13页

第4页 / 共13页

第5页 / 共13页

第6页 / 共13页

第7页 / 共13页

第8页 / 共13页

2023 年山西长治中考数学真题及答案第Ⅰ卷选择题（共 30 分）一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑） 1. 计算   3 1     A. 3 ）．的结果为（ 1 3 B. C. 3 D. 4 2. 全民阅读有助于提升一个国家、一个民族的精神力量．图书馆是开展全民阅读的重要场所．以下是我省四个地市的图书馆标志，其文字上方的图案是轴对称图形的是（） A. B. C. D. 3. 下列计算正确的是（） A. 2 a a  3  6 a B.   3 a b 2   6 a b 2 C. 6 a  3 a  2 a D.  32 a 6 a 4. 山西是全国电力外送基地，2022 年山西省全年外送电量达到 1464 亿千瓦时，同比增长18.55% ．数据 1464 亿千瓦时用科学记数法表示为（） A. 1.464 10 千瓦时 8 C. 11 1.464 10 千瓦时 B. 1464 10 千瓦时 8 D. 1.464 10 千瓦时 12 5. 如图，四边形 ABCD 内接于 ,  O AC BD , 为对角线， BD 经过圆心O ．若 BAC 40 = ，则 DBC 的  度数为（）

A. 40 B. 50 C. 60 D. 70 6. 一种弹簧秤最大能称不超过10kg 的物体，不挂物体时弹簧的长为12cm ，每挂重1kg 物体，弹簧伸长 0.5cm ．在弹性限度内，挂重后弹簧的长度  cmy  与所挂物体的质量  x kg 之间的函数关系式为（） A. y  12 0.5  x B. y  12 0.5  x C. y  10 0.5  x D. y  0.5 x 7. 如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心O 的光线相交于点 P ，点 F 为焦点．若 1 155 , 2 30       ，则 3 的度数为（） A. 45 B. 50 C. 55 D. 60 8. 已知 ( 2, ), a B A  ( 1, ),  (3, ) b C c 都在反比例函数 y  的图象上，则 a、b、c的关系是（ 4 x ）

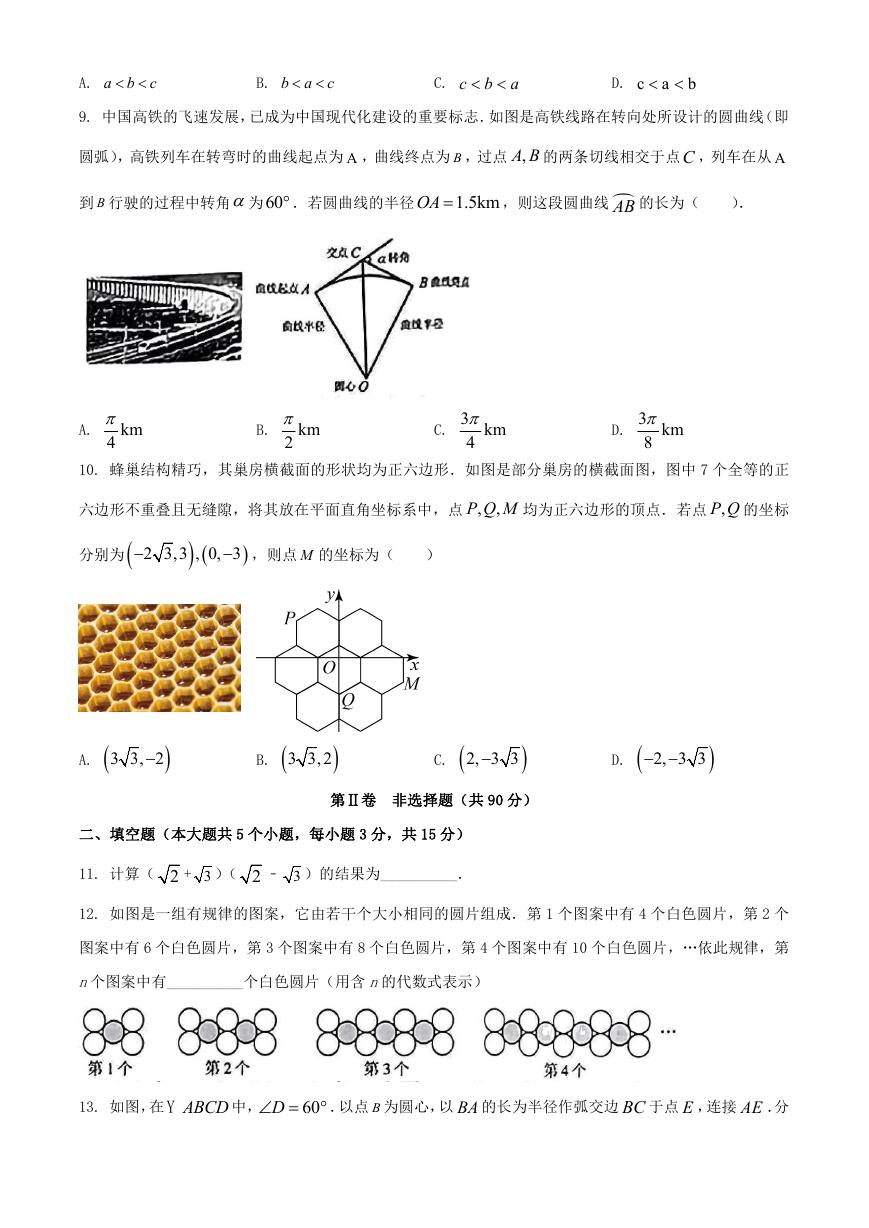
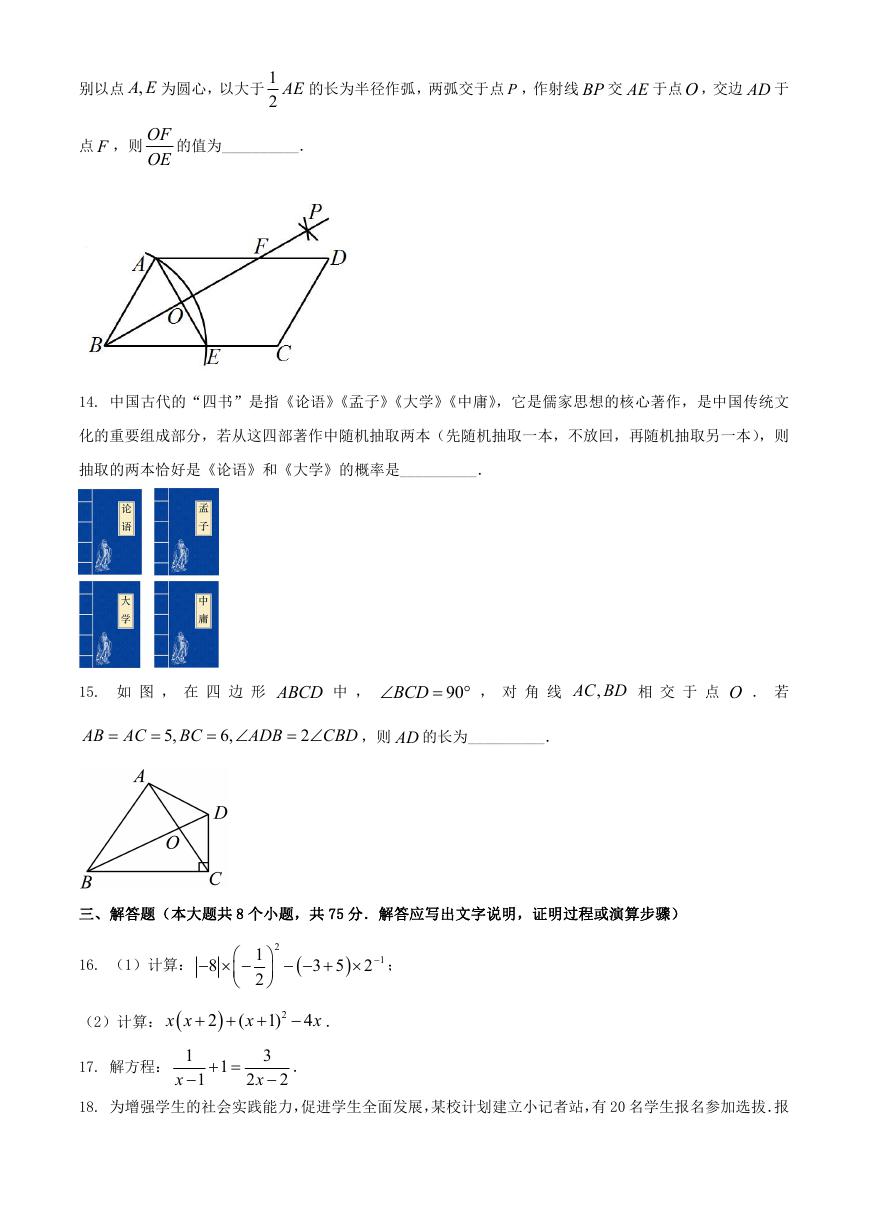
A. a b c   B. b a c   C. c   b a D. c   a b 9. 中国高铁的飞速发展，已成为中国现代化建设的重要标志．如图是高铁线路在转向处所设计的圆曲线（即圆弧），高铁列车在转弯时的曲线起点为 A ，曲线终点为 B ，过点 ,A B 的两条切线相交于点C ，列车在从 A 到 B 行驶的过程中转角为60 ．若圆曲线的半径 OA  1.5km ，则这段圆曲线 AB 的长为（）． A.  4 km B.  2 km C. 3 km  4 D. 3 km  8 10. 蜂巢结构精巧，其巢房横截面的形状均为正六边形．如图是部分巢房的横截面图，图中 7 个全等的正 ,P Q M 均为正六边形的顶点．若点 ,P Q 的坐标六边形不重叠且无缝隙，将其放在平面直角坐标系中，点 , 分别为  ，则点 M 的坐标为（   ）  2 3,3 , 0, 3  A.  3 3, 2  B.  3 3,2  C.  2, 3 3   D.  2, 3 3    第Ⅱ卷非选择题（共 90 分）二、填空题（本大题共 5 个小题，每小题 3 分，共 15 分） 11. 计算（ 2 + 3 ）（ 2 ﹣ 3 ）的结果为__________． 12. 如图是一组有规律的图案，它由若干个大小相同的圆片组成．第 1 个图案中有 4 个白色圆片，第 2 个图案中有 6 个白色圆片，第 3 个图案中有 8 个白色圆片，第 4 个图案中有 10 个白色圆片，…依此规律，第 n个图案中有__________个白色圆片（用含 n的代数式表示） 13. 如图，在 ABCD Y 中， D  60  ．以点 B 为圆心，以 BA 的长为半径作弧交边 BC 于点 E ，连接 AE ．分

别以点 ,A E 为圆心，以大于 1 2 AE 的长为半径作弧，两弧交于点 P ，作射线 BP 交 AE 于点O ，交边 AD 于点 F ，则 OF OE 的值为__________． 14. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》，它是儒家思想的核心著作，是中国传统文化的重要组成部分，若从这四部著作中随机抽取两本（先随机抽取一本，不放回，再随机抽取另一本），则抽取的两本恰好是《论语》和《大学》的概率是__________． 15. 如图，在四边形 ABCD 中， BCD  90  ，对角线 ,AC BD 相交于点 O ．若 AB AC   5, BC   6, ADB   2 CBD ，则 AD 的长为__________．三、解答题（本大题共 8 个小题，共 75 分．解答应写出文字说明，证明过程或演算步骤） 16. （1）计算： 8       2 1 2     3 5      2 1  ；（2）计算：  x x 1  17. 解方程： x 1   1 2  2   ( x 2  ． 4 x  1) 3 x  2 ． 18. 为增强学生的社会实践能力，促进学生全面发展，某校计划建立小记者站，有 20 名学生报名参加选拔．报

名的学生需参加采访、写作、摄影三项测试，每项测试均由七位评委打分（满分 100 分），取平均分作为该项的测试成绩，再将采访、写作、摄影三项的测试成绩按 4 4 2∶ ∶ 的比例计算出每人的总评成绩．小悦、小涵的三项测试成绩和总评成绩如下表，这 20 名学生的总评成绩频数直方图（每组含最小值，不含最大值）如下图测试成绩/分选手总评成绩/分采访写作摄影小悦 83 小涵 86 72 84 80 ▲ 78 ▲ （1）在摄影测试中，七位评委给小涵打出的分数如下：67，72，68，69，74，69，71．这组数据的中位数是__________分，众数是__________分，平均数是__________分；（2）请你计算小涵的总评成绩；（3）学校决定根据总评成绩择优选拔 12 名小记者．试分析小悦、小涵能否入选，并说明理由． 19. 风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞．该大桥限重标志牌显示，载重后总质量超过 30 吨的车辆禁止通行．现有一辆自重 8 吨的卡车，要运输若干套某种设备，每套设备由 1 个 A部件和 3 个 B部件组成，这种设备必须成套运输．已知 1 个 A部件和 2 个 B部件的总质量为 2.8 吨，2 个 A部件和 3 个 B部件的质量相等．

（1）求 1 个 A部件和 1 个 B部件的质量各是多少；（2）卡车一次最多可运输多少套这种设备通过此大桥？ 20. 2023 年 3 月，水利部印发《母亲河复苏行动河湖名单（2022－2025 年）》，我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选．在推进实施母亲河复苏行动中，需要砌筑洛种驳岸（也叫护坡）．某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动，利用课余时间完成了实践调查，并形成了如下活动报告．请根据活动报告计算 BC 和 AB 的长度（结果精确到 0.1m ．参考数据： 3 1.73  ， 2  1.41 ）．母亲河驳岸的调研与计算资料查阅、水利部门走访、实地查看了解课题调查方式功能驳岸是用来保护河岸，阻止河岸崩塌或冲刷的构筑物相关数据及说明，图中，点 A，B，C，D，E在同一竖直平面内， AE 与 CD 均与地面平行，岸墙 AB BCD EDC  ，  ，  60 AE 6m  135 3.5m CD  于点 A， ED  ， AE  1.5m ，驳岸剖面图计算

结果交流展示 21. 阅读与思考：下面是一位同学的数学学习笔记，请仔细阅读并完成相应任务．瓦里尼翁平行四边形我们知道，如图 1，在四边形 ABCD 中，点 , E F G H 分别是边 , AB BC CD ， DA 的中点，顺次连接 , , , , E F G H ，得到的四边形 EFGH 是平行四边形． , , 我查阅了许多资料，得知这个平行四边形 EFGH 被称为瓦里尼翁平行四边形．瓦里尼翁  Varingnon Pierre，－是法国数学家、力学家．瓦里尼翁平行四边形与原四边形关系密切． 1654 1722  ①当原四边形的对角线满足一定关系时，瓦里尼翁平行四边形可能是菱形、矩形或正方形． ②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系． ③瓦里尼翁平行四边形的面积等于原四边形面积的一半．此结论可借助图 1 证明如下：证明：如图 2，连接 AC ，分别交 ,EH FG 于点 ,P Q ，过点 D 作 DM AC 于点 M ，交 HG于点 N ． ∵ ,H G 分别为 ,AD CD 的中点，∴ HG AC HG ∥ ,  1 2 AC ．（依据 1）

∴ DN DG NM GC  ．∵ DG GC ，∴ DN NM   1 2 DM ． ∵四边形 EFGH 是瓦里尼翁平行四边形，∴ HE GF∥ ，即 HP GQ∥ ． ∵ HG AC∥ ，即 HG PQ∥ ， ∴四边形 HPQG 是平行四边形．（依据 2）∴ S  ∵ S △ ADC  1 2 任务： AC DM HG DM    ，∴ S  HPQG  HG MN   1 2 HG DM  ． △ ．同理，… ADC HPQG 1 2 S （1）填空：材料中的依据 1 是指：_____________．依据 2 是指：_____________．（2）请用刻度尺、三角板等工具，画一个四边形 ABCD 及它的瓦里尼翁平行四边形 EFGH ，使得四边形 EFGH 为矩形；（要求同时画出四边形 ABCD 的对角线）（3）在图 1 中，分别连接 ,AC BD 得到图 3，请猜想瓦里尼翁平行四边形 EFGH 的周长与对角线 ,AC BD 长度的关系，并证明你的结论． 22. 问题情境：“综合与实践”课上，老师提出如下问题：将图 1 中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为 ABC 和 DFE△ ，其中  ACB   DEF  90 ,     ．将 ABC D A 和按图 2 所示方式摆放，其中点 B 与点 F 重合（标记为点 B ）．当 ABE DFE△ 点G ．试判断四边形 BCGE 的形状，并说明理由．    时，延长 DE 交 AC 于 A

资料库

2023年山西长治中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料