2022年青海果洛中考数学真题及答案.doc-资料库

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

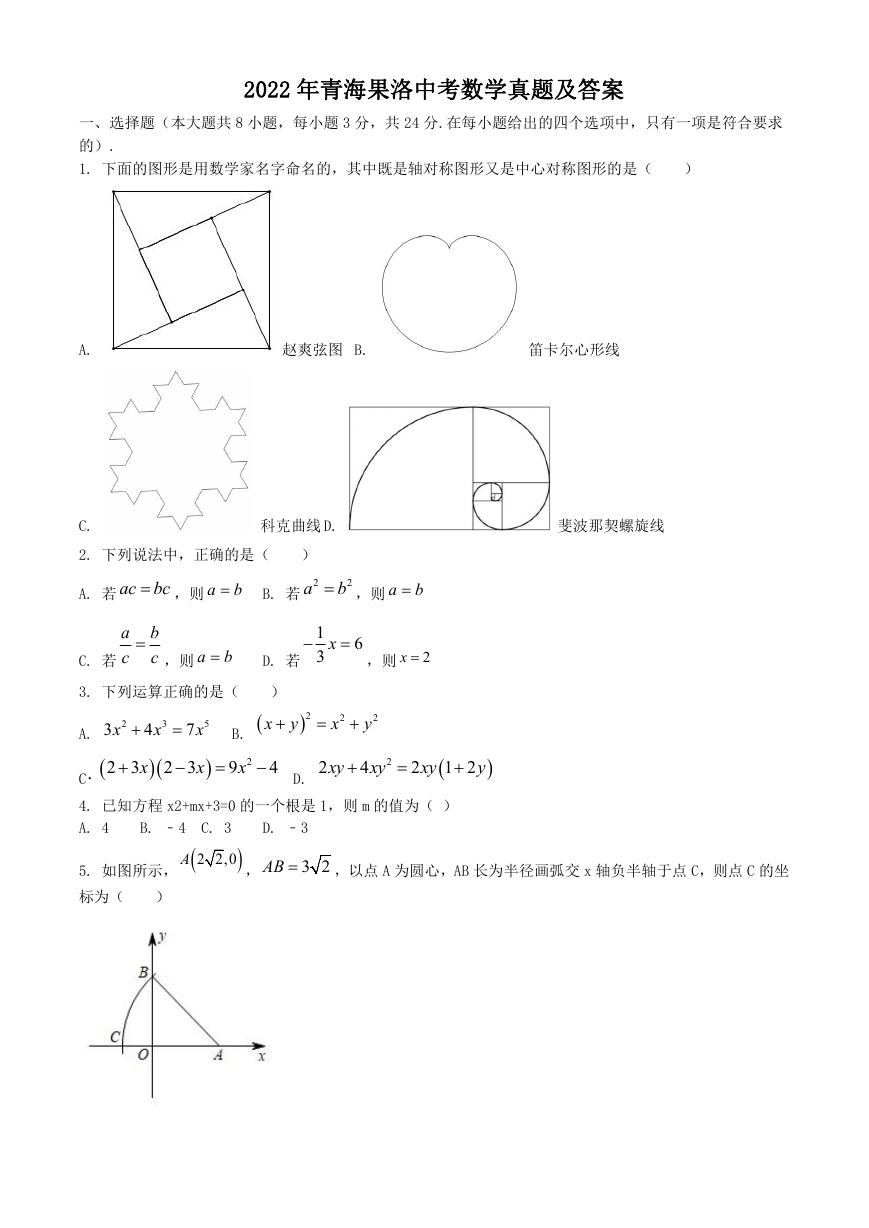
2022 年青海果洛中考数学真题及答案一、选择题（本大题共 8 小题，每小题 3 分，共 24 分.在每小题给出的四个选项中，只有一项是符合要求的）. 1. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（） A. C. 赵爽弦图 B. 笛卡尔心形线科克曲线 D. 斐波那契螺旋线 2. 下列说法中，正确的是（） A. 若 ac bc ，则 a b B. 若 2 a 2 b ，则 a b a c  b c C. 若，则 a b D. 若 1 x 3  6 ，则 2 x  3. 下列运算正确的是（） A. 3 C.  4 x  B.  9 x  2 2 x  3  5 7 x x  y 2  2 x  2 y 2 3  x 2 3  x   4 D. 2 xy  2 4 xy  2 xy  1 2  y  4. 已知方程 x2+mx+3=0 的一个根是 1，则 m 的值为（） A. 4 B. ﹣4 D. ﹣3 C. 3 5. 如图所示，  A 2 2,0  AB  3 2 ，标为（），以点 A 为圆心，AB 长为半径画弧交 x 轴负半轴于点 C，则点 C 的坐

A.  3 2,0  B.  2,0 C.   2,0 D.   3 2,0  6. 数学课上老师用双手形象的表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）.从左至右依次表示（） A. 同旁内角、同位角、内错角 B. 同位角、内错角、对顶角 C. 对顶角、同位角、同旁内角 D. 同位角、内错角、同旁内角 7. 如图，在 Rt ABC△ 中， ACB  90  ，D 是 AB 的中点，延长 CB 至点 E，使 BE BC ，连接 DE，F 为 DE 中点，连接 BF.若 AC  ， 16 BC  ，则 BF 的长为（ 12 ） C. 6 B. 4 A. 5 8. 2022 年 2 月 5 日，电影《长津湖》在青海剧场首映，小李一家开车去观看.最初以某一速度匀速行驶，中途停车加油耽误了十几分钟，为了按时到达剧场，小李在不违反交通规则的前提下加快了速度，仍保持匀速行驶.在此行驶过程中，汽车离剧场的距离 y（千米）与行驶时间 t（小时）的函数关系的大致图象是（ D. 8 ） A. C. B. D. 二、填空题（本大题共 12 小题，每小题 2 分，共 24 分）. 9. －2022 的相反数是______．

1 1x  有意义，则实数 x 的取值范围是______. 10. 若式子 11. 习近平总书记指出“善于学习，就是善于进步”.“学习强国”平台上线的某天，全国大约有 124600000 人在平台上学习，将这个数据用科学记数法表示为______. x 2 4 0       3 6 x  12. 不等式组的所有整数解的和为______. 13. 由若干个相同的小正方体构成的几何体的三视图如图所示，那么构成这个几何体的小正方体的个数是 ______. 14. 如图，一块砖的 A，B，C 三个面的面积之比是 5：3：1，如果 A，B，C 三个面分别向下在地上，地面所受压强分别为 1P ， 2P ， 3P ，压强的计算公式为 FP  S ，其中 P 是压强，F 是压力，S 是受力面积，则 1P ， 2P ， 3P 的大小关系为______（用小于号连接）. 15. 如图，在 Rt ABC 中，∠B=90°，ED 是 AC 的垂直平分线，交 AC 于点 D，交 BC 于点 E．已知∠BAE=10°，则∠C 的度数为_____________°． 16. 如图矩形 ABCD的对角线 AC 和 BD 相交于点 O，过点 O 的直线分别交 AD 和 BC 于点 E，F，AB＝3，BC＝4，则图中阴影部分的面积为_____． 17. 如图是一个隧道的横截面，它的形状是以点 O 为圆心的圆的一部分，如果 C 是 O 中弦 AB 的中点，CD 经过圆心 O 交 O 于点 D，并且 AB  4m ， CD  ，则 O 的半径长为______m． 6m

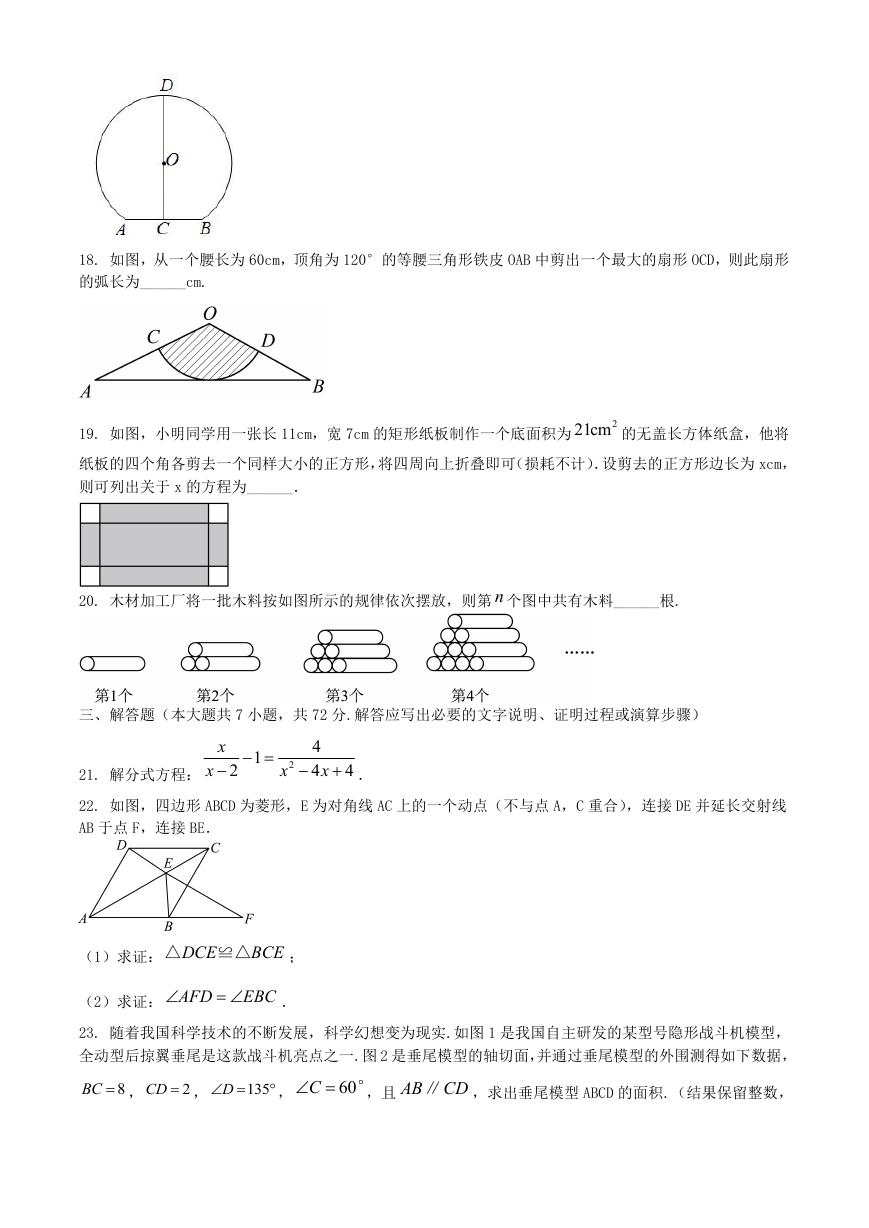
18. 如图，从一个腰长为 60cm，顶角为 120°的等腰三角形铁皮 OAB 中剪出一个最大的扇形 OCD，则此扇形的弧长为______cm. 19. 如图，小明同学用一张长 11cm，宽 7cm 的矩形纸板制作一个底面积为 21cm 的无盖长方体纸盒，他将 2 纸板的四个角各剪去一个同样大小的正方形，将四周向上折叠即可（损耗不计）．设剪去的正方形边长为 xcm，则可列出关于 x 的方程为______． 20. 木材加工厂将一批木料按如图所示的规律依次摆放，则第 n 个图中共有木料______根. 三、解答题（本大题共 7 小题，共 72 分.解答应写出必要的文字说明、证明过程或演算步骤） 21. 解分式方程： x  x 2 1   4 4 2 x  x  ． 4 22. 如图，四边形 ABCD 为菱形，E 为对角线 AC 上的一个动点（不与点 A，C 重合），连接 DE 并延长交射线 AB 于点 F，连接 BE．（1）求证： DCE △ ≌△ BCE ；（2）求证： AFD    EBC ． 23. 随着我国科学技术的不断发展，科学幻想变为现实.如图 1 是我国自主研发的某型号隐形战斗机模型，全动型后掠翼垂尾是这款战斗机亮点之一.图 2 是垂尾模型的轴切面，并通过垂尾模型的外围测得如下数据， C  °，且 AB CD∥ ，求出垂尾模型 ABCD 的面积.（结果保留整数， BC  ， D  CD  ， 2 8 135  ， 60

参考数据： 2  1.414 ， 3 1.732  ） 24. 如图，AB 是 O 的直径，AC 是 O 的弦，AD 平分∠CAB 交 O 于点 D，过点 D 作 O 的切线 EF，交 AB 的延长线于点 E，交 AC 的延长线于点 F．（1）求证： AF EF ；（2）若 CF  ， 1 AC  ， 2 AB  ，求 BE 的长． 4 25. 为迎接党的二十大胜利召开，某校对七、八年级的学生进行了党史学习宣传教育，其中七、八年级的学生各有 500 人.为了解该校七、八年级学生对党史知识的掌握情况，从七、八年级学生中各随机抽取 15 人进行党史知识测试，统计这部分学生的测试成绩（成绩均为整数，满分 10 分，8 分及 8 分以上为优秀），相关数据统计、整理如下：七年级抽取学生的成绩：6，6，6，8，8，8，8，8，8，8，9，9，9，9，10. 八年级抽取学生的测试成绩条形统计图七、八年级抽取学生的测试成绩统计表年级平均数七年级 8 八年级 8

众数中位数优秀率 a 8 80% （1）填空： a ______，b  ______； 7 b 60% （2）根据以上数据，你认为该校七、八年级中，哪个年级的学生党史知识掌握得较好？请说明理由（写出一条即可）；（3）请估计七、八年级学生对党史知识掌握能够达到优秀的总人数；（4）现从七、八年级获得 10 分的 4 名学生中随机抽取 2 人参加党史知识竞赛，请用列表法或画树状图法，求出被选中的 2 人恰好是七、八年级各 1 人的概率. 26. 两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等的三角形，把具有这个规律的图形称为“手拉手”图形. （1）问题发现：如图 1，若 ABC 是顶角相等的等腰三角形，BC，DE 分别是底边.求证： BD CE ；和 ADE  图 1 （2）解决问题：如图 2，若 ACB△ 和 DCE  均为等腰直角三角形，  ACB   DCE  90  ，点 A，D，E 在同一条直线上，CM 为 DCE  中 DE 边上的高，连接 BE，请判断∠AEB 的度数及线段 CM，AE，BE 之间的数量关系并说明理由. 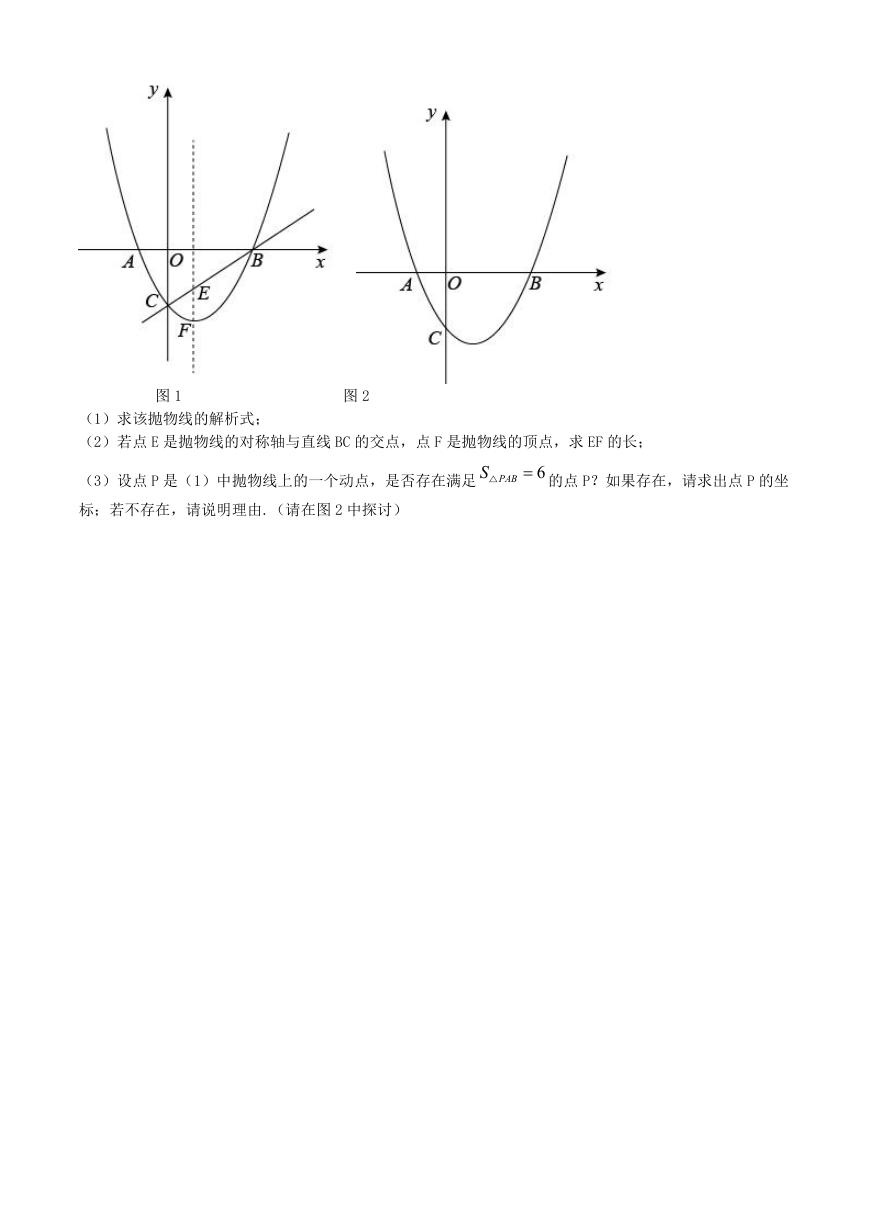图 2 27. 如图 1，抛物线 y  2 x  bx  与 x 轴交于  A  c 1,0 ，  B 3,0 两点，与 y 轴交于点 C.

图 1 图 2 （1）求该抛物线的解析式；（2）若点 E 是抛物线的对称轴与直线 BC 的交点，点 F 是抛物线的顶点，求 EF 的长；（3）设点 P 是（1）中抛物线上的一个动点，是否存在满足 S △ PAB  6 的点 P？如果存在，请求出点 P 的坐标；若不存在，请说明理由.（请在图 2 中探讨）

3.D 4.B 5.C 6.D 7.A 8.B 11. 1x  10 3 ## 13 3 12.0 8 1.246 10 18. 20 19.  13.5  x 11 2  7 2  14.  x  P P 1 2   21 20. P 3  n n  2 15.40  1 参考答案一、选择题 1.A 2.C 二、填空题 9.2022 10. 17. 16.6 三、解答题 21. x=4 25. （1） 22. （1）见解析 8a  ； 8b  （2）见解析 23.24 24. （1）见解析（2）2 （2）见解析  ； DCE 90  （3）700 人  AE AD DE BE   1 2 （4） 2 CM  26. （1）见解析 2 2  27（1）  y x （2） 3  x （2）2 （3）当点 P 的坐标分别为  1 0, 3 P   ，  2 2, 3 P   S △ PAB  6 时，，  3 1 P  7,3  ，  4 1 P  7,3 

资料库

2022年青海果洛中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料