logo资料库

K均值聚类算法PPT.pptx

发布时间：2022-06-19 发布人：admin 分类：说明书 资料大小：0.67M 资料格式：pptx 举报 版权申诉
第1页 / 共26页
第2页 / 共26页
第3页 / 共26页
第4页 / 共26页
第5页 / 共26页
第6页 / 共26页
第7页 / 共26页
第8页 / 共26页
资料共26页，剩余部分请下载后查看
    算 法 分 享 K-means聚类算法 xx 2017.8.15
    聚 类 所谓聚类问题，就是给定一个元素集合 D，其中每个元素具有n个可观察属性，使用 某种算法将D划分成k个子集，要求每个子集 内部的元素之间相异度尽可能低，而不同子集 的元素相异度尽可能高。其中每个子集叫做一 个簇。
    目录 CATALOG 算法原理 算法流程 实例讲解 应用场景 算法总结 改进算法
    01 基本原理
    01 0 2 0 3 0 4 05 标量 标量也就是无方向意义的数字，也叫 标度变量 二元变量 二元变量是只能取0和1两种值变量， 通常用来标识是或不是这种二值属性 分类变量 分类变量是二元变量的推广，类似于 程序中的枚举变量 序数变量 序数变量是具有序数意义的分类变量， 通常可以按照一定顺序意义排列 向量 有大小而且有方向
    欧几里 得距离 曼哈顿 距离 闵可夫 斯基距 离 在m维空间中两个点之间的真实距离，或者向量的自然长度（即该 点到原点的距离）。例：X1（3，4，5）与X2（7，4，8）的距 离为 5 在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的 投影的距离总和。例： X1（3，4，5）与X2（7，4，8）的距 离为 7 闵可夫斯基距离是欧几里得距离和曼哈顿距离的推广。例：p=1时 为欧几里得距离，p=2时为曼哈顿距离 归一化： 例：一组点 X 到种子点 （1，1）的最大距离为 11，最小距离为1，其中 X1(5,4)到到种子点距离 为5，归一化后为0.5.
    取值不同的同位属性数/单 个元素的属性位数 设有X={1,0,0,0,1,0,1,1}， Y={0,0,0,1,1,1,1,1}，可以看到， 两个元素第2、3、5、7和8个属 性取值相同，而第1、4和6个取 值不同，那么相异度可以标识为 3/8=0.375。 取值不同的同位属性数/(单个 元素的属性位数-同取0的位数) 设有X={1,0,0,0,1,0,1,1}， Y={0,0,0,1,1,1,1,1}，可以看到，两 个元素第2、3、5、7和8个属性取 值相同，而第1、4和6个取值不同， 第2、3个属性取值相同，那么相 异度可以标识为3/(8-2)=0.5。这 也叫做非对称二元相异度
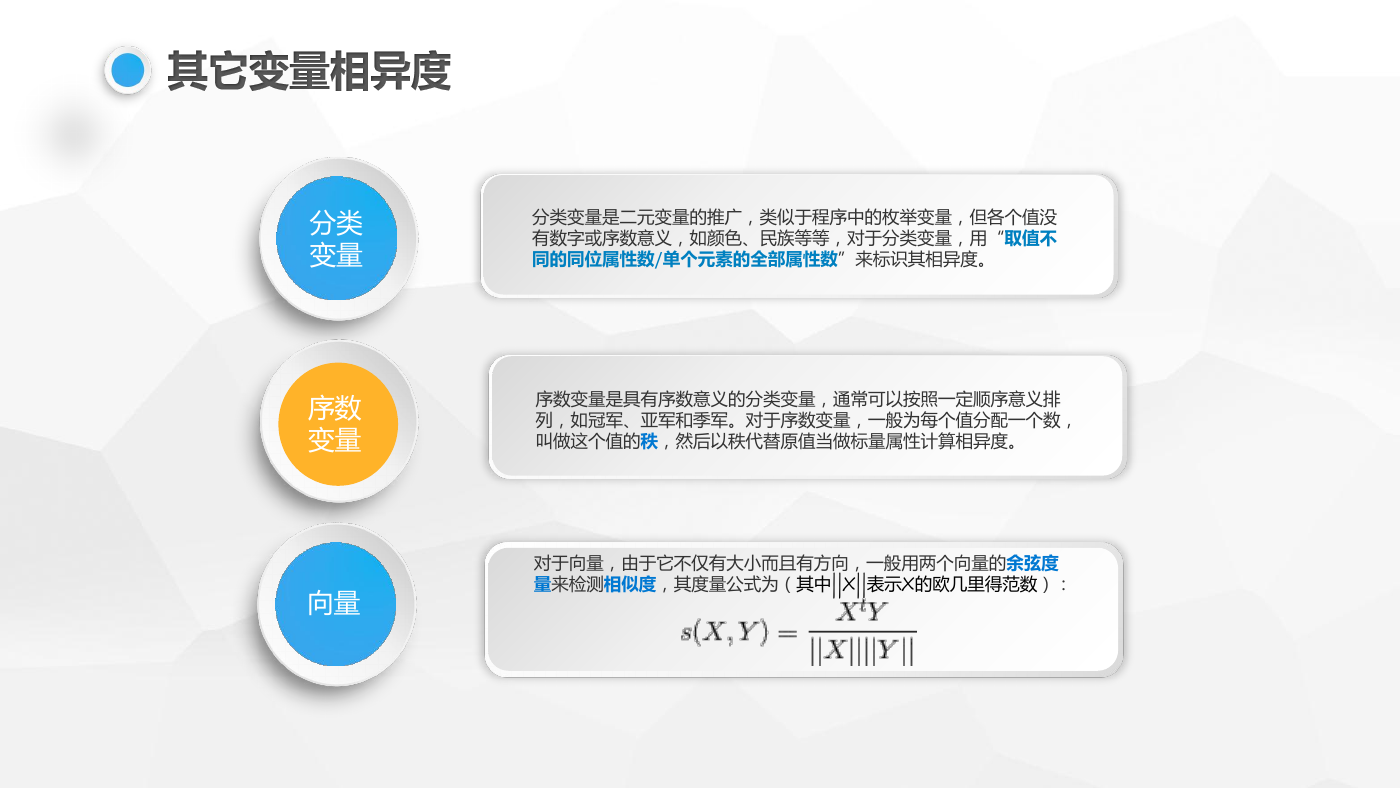
    分类 变量 序数 变量 向量 分类变量是二元变量的推广，类似于程序中的枚举变量，但各个值没 有数字或序数意义，如颜色、民族等等，对于分类变量，用“取值不 同的同位属性数/单个元素的全部属性数”来标识其相异度。 序数变量是具有序数意义的分类变量，通常可以按照一定顺序意义排 列，如冠军、亚军和季军。对于序数变量，一般为每个值分配一个数， 叫做这个值的秩，然后以秩代替原值当做标量属性计算相异度。 对于向量，由于它不仅有大小而且有方向，一般用两个向量的余弦度 量来检测相似度，其度量公式为（其中||X||表示X的欧几里得范数）：
    分享到：
    赞 收藏

    相关推荐

    资料库

    人工智能

    共收录2047份资料，累计62个分类，关注成员有19位，主要包括：GNSS,Pico-SIM868-GSM,GPRS,NB-IoT,GPRSHAT,SIM7070GCat-M,GNSSHAT,GSM,NB-IoTHAT,SIM7080GCat-M,R800CGSM,SIM800CGSM,UPSPowerModule(B),UPSPowerModule,Pico-SIM7020C-NB-IoT,SIM7028NB-IoTHAT,SIM7020CNB-IoTHAT,SIM7000XNB-IoTHAT,A7670CCat-1HAT,A7600C1Cat-1,SIM7600X4G&LTECat-1HAT,SIM7600X4GDONGLE用户手册,RM520N-GL5GHAT,RM500Q-GL5GHAT,RM500U-CN5GHAT,SIM820X-M25GforJetsonNano,AudioCardforJetsonNano,SIM7600G-H4GforJetsonNano,OpenNCC-Lite-4G8M,IMX219-77Camera,13.3inche-PaperHAT,10.3inche-PaperHAT(D),10.3inche-PaperHAT,9.7inche-PaperHAT,7.8inche-PaperHAT,6inchHDTouche-PaperHAT,6inchHDe-PaperHAT,6inche-PaperHAT,5.83inche-PaperHAT(C),LCD-Clock-A,0.95inchRGBOLED(A),0.96inchRGBOLEDModule,0.96inchOLEDModule,0.96inchOLED(A),1.27inchRGBOLEDModule,1.3inchOLEDModule(C),1.3inchOLED(A),1.32inchOLEDModule,1.5inchRGBOLEDModule,1.5inchOLEDModule,JETSONORINNX,自然语言处理,搜索引擎,VR,计算广告,深度学习,机器学习

    热门标签

    GNSS Pico-SIM868-GSM GPRS NB-IoT GPRSHAT SIM7070GCat-M GNSSHAT GSM NB-IoTHAT SIM7080GCat-M R800CGSM SIM800CGSM UPSPowerModule(B) UPSPowerModule Pico-SIM7020C-NB-IoT SIM7028NB-IoTHAT SIM7020CNB-IoTHAT SIM7000XNB-IoTHAT A7670CCat-1HAT A7600C1Cat-1 SIM7600X4G&LTECat-1HAT SIM7600X4GDONGLE用户手册 RM520N-GL5GHAT RM500Q-GL5GHAT RM500U-CN5GHAT SIM820X-M25GforJetsonNano AudioCardforJetsonNano SIM7600G-H4GforJetsonNano OpenNCC-Lite-4G8M IMX219-77Camera 13.3inche-PaperHAT 10.3inche-PaperHAT(D) 10.3inche-PaperHAT 9.7inche-PaperHAT 7.8inche-PaperHAT 6inchHDTouche-PaperHAT 6inchHDe-PaperHAT 6inche-PaperHAT 5.83inche-PaperHAT(C) LCD-Clock-A 0.95inchRGBOLED(A) 0.96inchRGBOLEDModule 0.96inchOLEDModule 0.96inchOLED(A) 1.27inchRGBOLEDModule 1.3inchOLEDModule(C) 1.3inchOLED(A) 1.32inchOLEDModule 1.5inchRGBOLEDModule 1.5inchOLEDModule JETSONORINNX 自然语言处理 搜索引擎 VR 计算广告 深度学习 机器学习

    最新资料