演化计算-用于全局优化多峰函数的综合学习粒子群优化算法.docx-资料库

a1742326479-10542151-4744302543364381596.docx.pdf-第1页.png

第1页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第2页.png

第2页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第3页.png

第3页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第4页.png

第4页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第5页.png

第5页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第6页.png

第6页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第7页.png

第7页 / 共22页

a1742326479-10542151-4744302543364381596.docx.pdf-第8页.png

第8页 / 共22页

自然计算与应用课程演化计算报告院系：电子科学与技术系学号： SC17023133 姓名：陈文卿

用于全局优化多模式函数的综合学习粒子群优化算法作者：J. J. Liang, A. K. Qin, Student Member, IEEE, Ponnuthurai Nagaratnam Suganthan, Senior Member, IEEE, and S. Baskar Abstract—This paper presents a variant of particle swarm optimizers (PSOs) that we call the comprehensive learning particle swarm optimizer (CLPSO), which uses a novel learning strategy whereby all other particles’ historical best information is used to update a particle’s velocity. This strategy enables the diversity of the swarm to be preserved to discourage premature convergence. Experiments were conducted on multimodal test functions such as Rosenbrock, Griewank, Rastrigin, Ackley,and Schwefel and composition functions both with and without coordinate rotation. The results demonstrate good performance of the CLPSO in solving multimodal problems when compared with eight other recent variants of the PSO.Index Terms—Composition benchmark functions, comprehensive learning particle swarm optimizer (CLPSO), global numerical optimization, particle swarm optimizer (PSO). 摘要本文介绍了粒子群优化器（PSO）的一种变体，我们将其称为综合学习粒子群优化器（CLPSO），它使用一种新颖的学习策略，其中所有其他粒子的历史最佳信息用于更新粒子的速度。该策略使得能够保持群的多样性以防止过早收敛。在多模式测试函数上进行了实验，例如 Rosenbrock，Griewank，Rastrigin，Ackley 和 Schwefel 以及有和没有坐标旋转的组合函数。结果表明，与 PSO 的其他八个变体相比，CLPSO 在解决多模式问题方面具有良好的性能。关键词：组合基准函数，综合学习粒子群优化器（CLPSO），全局数值优化，粒子群优化器（PSO）。一、预备知识无约束优化问题可以表述为一个 D 维的最小化问题，如下所示： PSO 模仿昆虫、动物、鸟类和鱼类学校的群体行为，这些群体以协作的方式寻找食物。群中的每个成员通过学习自己的经验和其他成员的经历来调整其搜索模式。人们研究了这些现象并构建了数学模型。 1、传统 PSO

(1) 为第 d 维的第 i 个粒子的速度，为第 d 维的第 i 个粒子的位置。 pbesti 是当前第 i 个粒子中，拥有最好的适度应值的位置。 gbest 是群体中的最佳位置 c1 和 c2 分别是将每个粒子导向 pbest 和 gbest 位置的随机加速常数。和是两个在【0,1】之间的随机数。有的学者用以下公式：（2）公式 1 有更大的搜索空间，因为独立地更新每个维度。公式 2 的搜索空间小些，因为相同的随机数被所有维度共用。二、PSO 的变形其中一种变形引进了一种叫做惯性的参数 w：参数 w 是用来平衡全局和局部参数。大的 w 适合全局参数，相反适合局部参数。三、综合学习 PSO 虽然有很多 PSO 的变形，但是过早收敛的问题仍然未解决。在原始 PSO 中，每个粒子都同时从 pbest 和 gbest 学习。将向社会学习方面限制其只与 gbest 有关使得原始 PSO 快速收敛。然而，因为群中的所有粒子都从中学习，即使当前 gbest 远离全局最优值，如果搜索环境由许多局部解混合构成，则粒子可能很容易被吸引到该区域并陷入局部最优。接下来有三种使用综合学习 PSO 方法并且显著提升效果的方法。新方法中我们采用如下的速度更新公式：定义了粒子 i 应该采用哪个粒子的 pbest, 可以是任何粒子的 pbest 所对应的维度,由概率 Pc 决定，也被叫做学习概率。对于粒子 i 的任何一个维度，都随机生成一个随机数.如果这个数字大于 Pc，相应的维度就会从自身的 pbest 学习。否则，将会从其他的粒子的 pbest 学习。当从其他粒子中学习时，我们使用以下的锦标赛删选步骤。（1）我们先从 population 中随机选择两个速度没有被更新的粒子（2）比较这两个粒子的适应度并选择更好的那个。在本算法（CLPSO）中，我

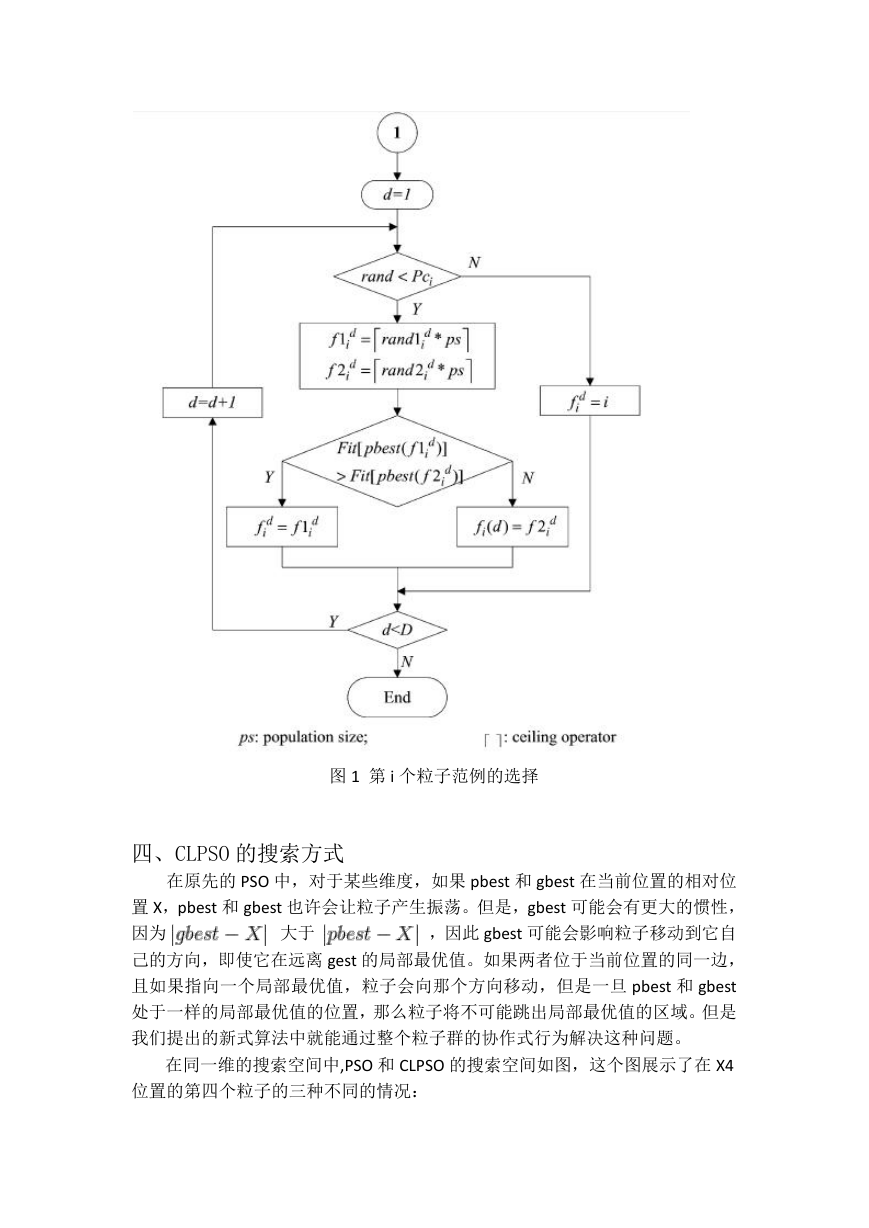
们定义适应度越大越好，这意味着当我们解决最小化问题的时候，我们会使用负函数的值作为适应度函数的值。（3）对于该维，我们使用胜者的 pbest 作为范例去学习。如果一个粒子的所有范例都是它自己的 pbest，我们会随机选择其中的一维去学习另一个粒子的对应该维的 pbest。求 fi 的细节如图。所有的都可以在搜索空间中利用从不同粒子的历史最佳位置中提取信息以生成新的位置，为了保证粒子从好的范例中学习并且最小化浪费在不好的方向的时间，我们让粒子从范例中学习直到增加至某些代，我们称之为更新代差 m，才停止更新。（1）所有的粒子 pbest 都能被作为导航粒子飞行方向的范例，而不是利用粒子自身的 pbests 和 gbests 作为范例。（2）总体中的每个粒子都可以从不同维的不同 pbests 中学习一些代，而不是所有维都从一样的范例粒子中学习。换句话说，一个粒子的每一维都会不同粒子的 pbest 中相应维中学习。（3）粒子中的每一维只从一个粒子中学习一些代。

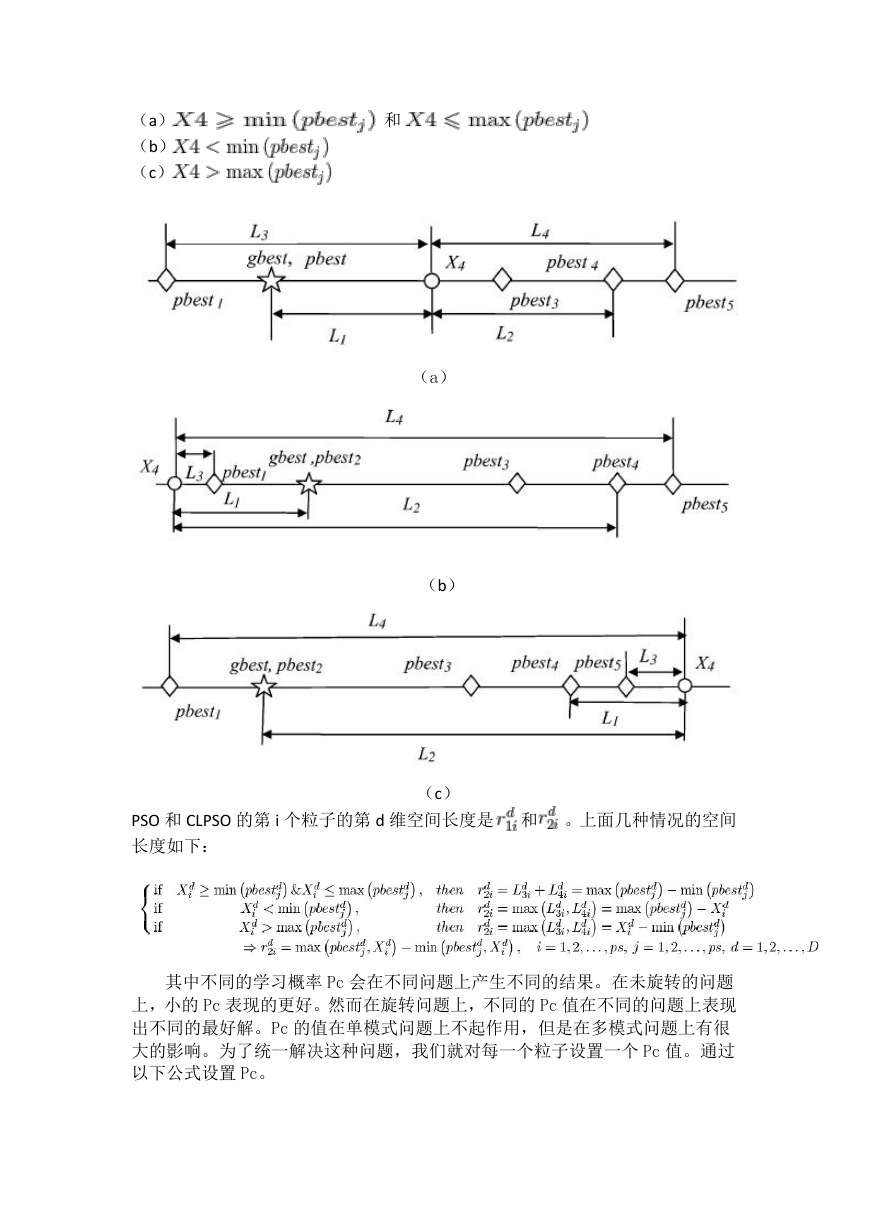
图 1 第 i 个粒子范例的选择四、CLPSO 的搜索方式在原先的 PSO 中，对于某些维度，如果 pbest 和 gbest 在当前位置的相对位置 X，pbest 和 gbest 也许会让粒子产生振荡。但是，gbest 可能会有更大的惯性，，因此 gbest 可能会影响粒子移动到它自因为己的方向，即使它在远离 gest 的局部最优值。如果两者位于当前位置的同一边，且如果指向一个局部最优值，粒子会向那个方向移动，但是一旦 pbest 和 gbest 处于一样的局部最优值的位置，那么粒子将不可能跳出局部最优值的区域。但是大于我们提出的新式算法中就能通过整个粒子群的协作式行为解决这种问题。在同一维的搜索空间中,PSO 和 CLPSO 的搜索空间如图，这个图展示了在 X4 位置的第四个粒子的三种不同的情况：

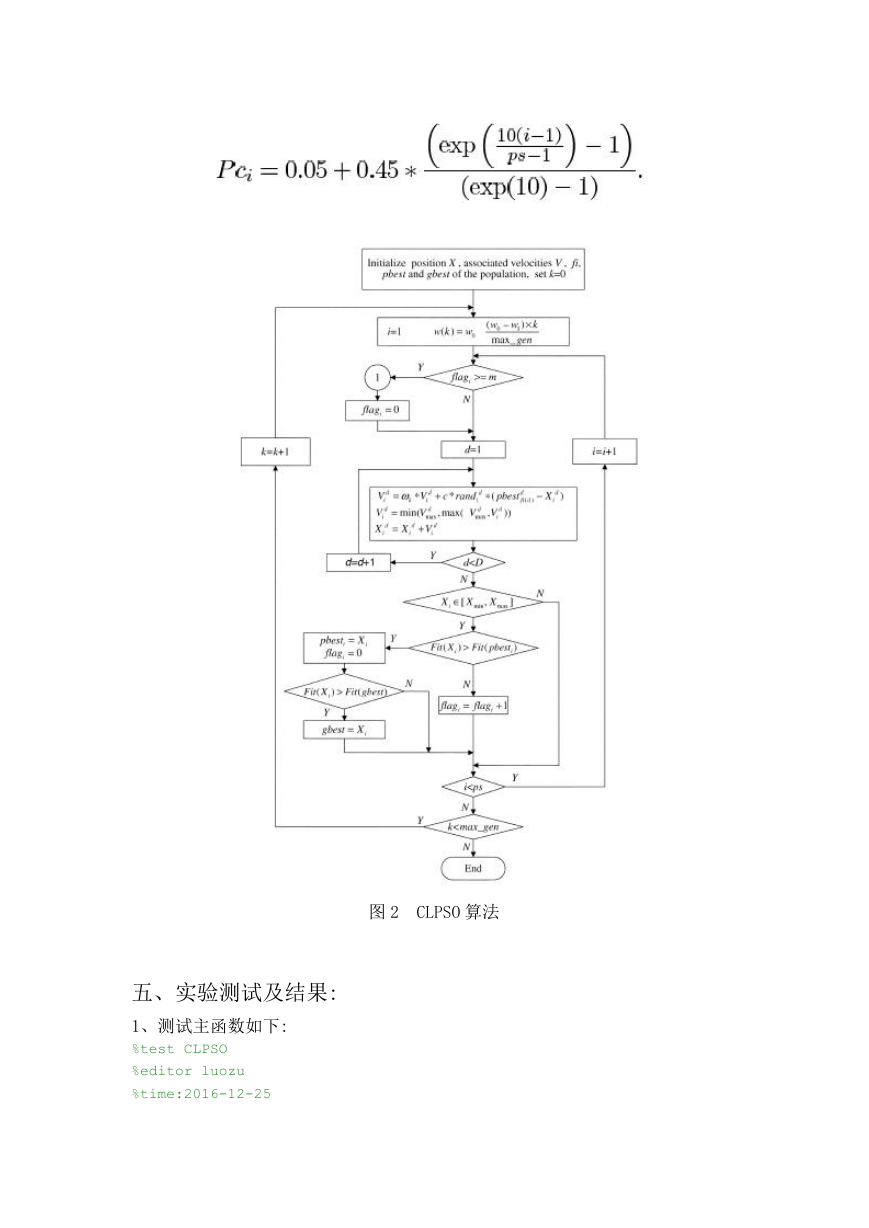
（a）（b）（c）和（a）（b）（c） PSO 和 CLPSO 的第 i 个粒子的第 d 维空间长度是和。上面几种情况的空间长度如下：其中不同的学习概率 Pc 会在不同问题上产生不同的结果。在未旋转的问题上，小的 Pc 表现的更好。然而在旋转问题上，不同的 Pc 值在不同的问题上表现出不同的最好解。Pc 的值在单模式问题上不起作用，但是在多模式问题上有很大的影响。为了统一解决这种问题，我们就对每一个粒子设置一个 Pc 值。通过以下公式设置 Pc。

图 2 CLPSO 算法五、实验测试及结果: 1、测试主函数如下: %test CLPSO %editor luozu %time:2016-12-25

%% %参数设置：w=0.9-0.4,c=1.49445,flag>=7(refreshing gap) clear all; clc; check_vel1=[]; position=[]; value=[]; real_iteration=[]; gbest_temp_val=[]; iteration=[]; num_FES=[]; gbest_val=[]; error_FES=[]; error_k=[]; fitness=[]; a=[];%画图 load Bounds; S=1;F=5;R=1; for i=S:F% problem for j=1:R fprintf('\nProblem =\t %d\n',i);%输出 % for j=1:30 % runs 每个benchmark函数运行30次 fprintf('run =\t %d\n',j) num_particle=40;range=Bounds(i,:);dimension=30;max_iteration=7500;max _FES=300000;func_num=i; [check_vel1,position(i,j,:),gbest_val(i,j,:),gbest_k_val(i,j,:),real_ iteration(i,j),iteration(i,j),num_FES(i,j),fitness(i,j,:),error_FES(i, j,:),error_k(i,j,:)]=CLPSO3(num_particle,range,dimension,max_iteratio n,max_FES,func_num); % figure(i),plot(error_log);xlabel('iteration','fontsize',12);ylabel('l og(Error)','fontsize',12); end file_name= [ 'CLPSO_PS_40_',num2str(i),'_30D_30runs.mat']; save (file_name); end %% error_k_log=log(error_k);%变成以e为底的数 error_FES_log=log(error_FES); for i=S:F%画图

资料库

演化计算-用于全局优化多峰函数的综合学习粒子群优化算法.docx

相关推荐

人工智能

热门标签

最新资料