logo资料库

数据集分析报告.docx

发布时间：2022-05-31 发布人：admin 分类：说明书 资料大小：0.91M 资料格式：docx 举报 版权申诉
第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
资料共19页，剩余部分请下载后查看
    机器学习中的算法实验性能以及算法优缺点分析
    一．Bagging与Boosting
    Bagging [1](bootstrap aggregating)是并行集成学习方法最著名的代表。
    Bagging，Boosting二者之间的区别：
    二．数据集分析
    三．实验：
    四．算法分析:
    五．三种模型的对比：
    六．参考文献
    机器学习中的算法实验性能以及算法优缺点分析 目录 一． Bagging 与 Boosting.....................................................................................................................................2 二． 数据集分析...................................................................................................................................................4 三． 实验：.........................................................................................................................................................12 四． 算法分析:...................................................................................................................................................14 五． 三种模型的对比：.....................................................................................................................................17 六． 参考文献.....................................................................................................................................................20
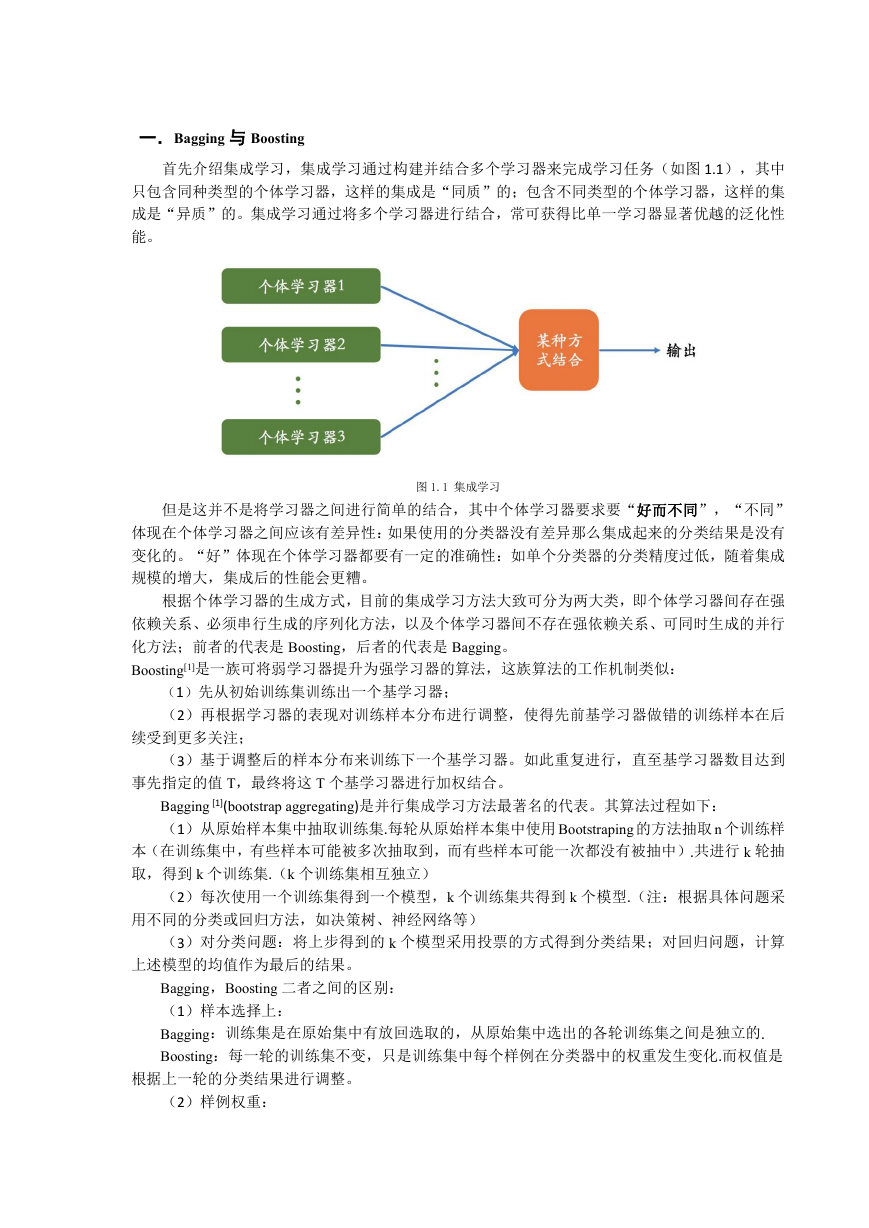
    一．Bagging 与 Boosting 首先介绍集成学习，集成学习通过构建并结合多个学习器来完成学习任务（如图 1.1），其中 只包含同种类型的个体学习器，这样的集成是“同质”的；包含不同类型的个体学习器，这样的集 成是“异质”的。集成学习通过将多个学习器进行结合，常可获得比单一学习器显著优越的泛化性 能。 图 1.1 集成学习 但是这并不是将学习器之间进行简单的结合，其中个体学习器要求要“好而不同”，“不同” 体现在个体学习器之间应该有差异性：如果使用的分类器没有差异那么集成起来的分类结果是没有 变化的。“好”体现在个体学习器都要有一定的准确性：如单个分类器的分类精度过低，随着集成 规模的增大，集成后的性能会更糟。 根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类，即个体学习器间存在强 依赖关系、必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系、可同时生成的并行 化方法；前者的代表是 Boosting，后者的代表是 Bagging。 Boosting[1]是一族可将弱学习器提升为强学习器的算法，这族算法的工作机制类似： （1）先从初始训练集训练出一个基学习器； （2）再根据学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后 续受到更多关注； （3）基于调整后的样本分布来训练下一个基学习器。如此重复进行，直至基学习器数目达到 事先指定的值 T，最终将这 T 个基学习器进行加权结合。 Bagging [1](bootstrap aggregating)是并行集成学习方法最著名的代表。其算法过程如下： （1）从原始样本集中抽取训练集.每轮从原始样本集中使用 Bootstraping 的方法抽取 n 个训练样 本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）.共进行 k 轮抽 取，得到 k 个训练集.（k 个训练集相互独立） （2）每次使用一个训练集得到一个模型，k 个训练集共得到 k 个模型.（注：根据具体问题采 用不同的分类或回归方法，如决策树、神经网络等） （3）对分类问题：将上步得到的 k 个模型采用投票的方式得到分类结果；对回归问题，计算 上述模型的均值作为最后的结果。 Bagging，Boosting 二者之间的区别： （1）样本选择上： Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的. Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化.而权值是 根据上一轮的分类结果进行调整。 （2）样例权重：
    Bagging：使用均匀取样，每个样例的权重相等。 Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。 （3）预测函数： Bagging：所有预测函数的权重相等。 Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。 （4）并行计算： Bagging：各个预测函数可以并行生成 Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果. （5）偏差和方差： bagging 是减少 variance，而 boosting 是减少 bias， bias 度量模型预测结果和真实结果的偏离程度，刻画模型算法本身的拟合能力， variance 度量同样大小的训练集的变动导致的学习能力的变化，刻画数据的分布情况造成影响。 二．数据集分析 2.1 所用数据集 进 行 分 析 的 数 据 集 分 别 是 pima-indians-diabetes 、 Breast-cancer-wisconsin 、 Lung_Cancer 、 Risk_factors_cervical_Risk、Statlog（Heart）[2]。 2.2 使用方法 相关性分析使用方法：相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系 的统计分析方法。例如，人的身高和体重之间；空气中的相对湿度与降雨量之间的相关关系都是相 关分析研究的问题。它是描述客观事物相互间关系的密切程度并用适当的统计指标表示出来的过 程。本论文中使用斯皮尔曼相关性系数方法计算每个数据集中任两列的相关程度并使用相关矩阵图 进行展示，颜色从红色渐变为蓝色。两变量之间得到的取值越大蓝色越深代表相关性越大。 缺失性分析使用方法：对每个数据集的数据缺失情况进行描述并使用柱状图进行展示，其中每 列的黑色柱体代表该列无缺失情况，其中白色部分代表该列的缺失情况，横轴是从 0 开始的数据集 的列数，竖轴代表缺失情况从 0 到 1。每列上的数字代表代表当前列无缺失的个数。针对数据集的 缺失情况,在进行实验时会进行初始填补. 噪点发现使用方法：噪声(noise)是被测量的变量的随机误差或方差。我们可以使用基本的数据 统计描述技术(例如，盒图或者散点图)和数据可视化方法来识别可能代表噪声的离群点，本论文中 使用散点图对数据集进行展示的时候，由于部分数据集维度过高，所以采用 PCA 统一降维至二维， 可能会对数据的结构性造成破坏，也由于 PCA 方法对空值敏感，所以先对数据集进行初始填补， 填补方法是众数填补即取缺失数据所在列出现最多次数的值填补缺失值，再进行降维。将降维得到 的数据使用 KMeans 聚类得到多个聚类再使用散点图在二维平面展示，查看数据的分布状况来发现 噪声数据的存在。 2.3 pima-indians-diabetes 数据集： 该数据集最初来自美国国家糖尿病、消化和肾脏疾病研究所。该数据集的目的是基于数据集中 包含的某些诊断测量值，诊断性地预测患者是否患有糖尿病。这些数据集总共有 768 条患者记录和 9 个属性，其中条件属性包括患者怀孕次数、体重指数、胰岛素水平、年龄等 8 个属性，最后一个 属性为决策属性为患者是否患有糖尿病。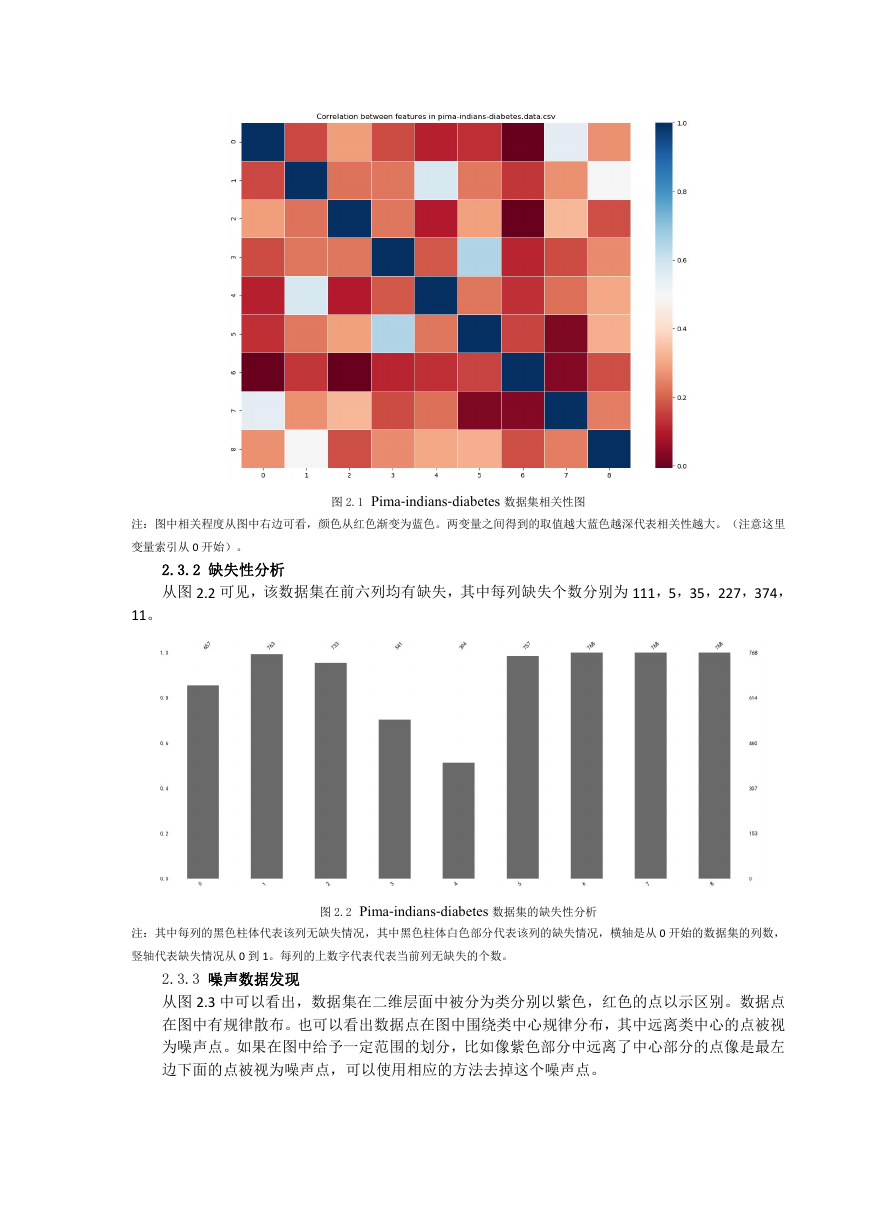 2.3.1 相关性分析 该数据集的相关性分析如下图（图 2.1）所示，可以从图中看出其中第 5 列和第 3 列，第 4 列 和第 1 列，第 7 列和第 0 列颜色偏蓝色，代表他们之间有较强的相关性。但是整体上看，该数据集 各个属性之间相关性不强。
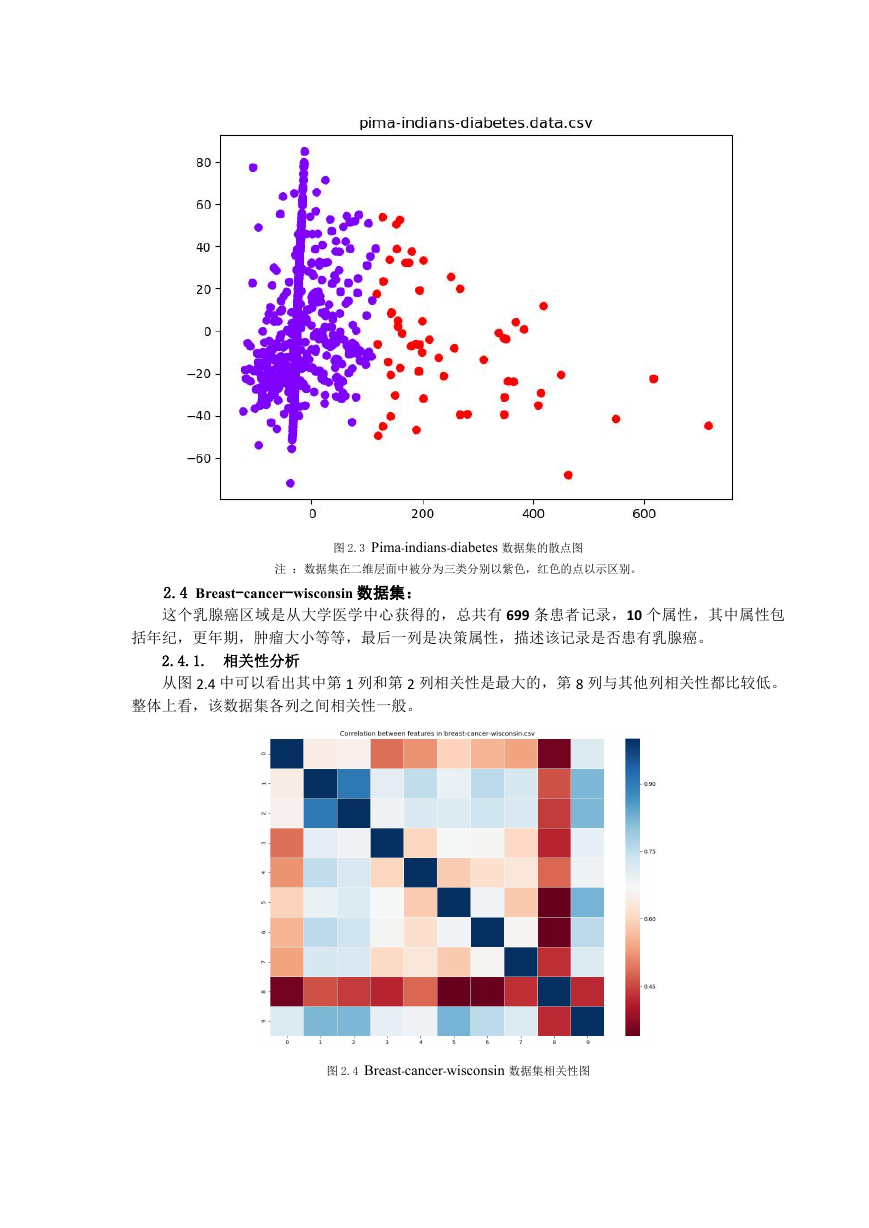
    注：图中相关程度从图中右边可看，颜色从红色渐变为蓝色。两变量之间得到的取值越大蓝色越深代表相关性越大。（注意这里 图 2.1 Pima-indians-diabetes 数据集相关性图 变量索引从 0 开始）。 2.3.2 缺失性分析 从图 2.2 可见，该数据集在前六列均有缺失，其中每列缺失个数分别为 111，5，35，227，374， 11。 图 2.2 Pima-indians-diabetes 数据集的缺失性分析 注：其中每列的黑色柱体代表该列无缺失情况，其中黑色柱体白色部分代表该列的缺失情况，横轴是从 0 开始的数据集的列数， 竖轴代表缺失情况从 0 到 1。每列的上数字代表代表当前列无缺失的个数。 2.3.3 噪声数据发现 从图 2.3 中可以看出，数据集在二维层面中被分为类分别以紫色，红色的点以示区别。数据点 在图中有规律散布。也可以看出数据点在图中围绕类中心规律分布，其中远离类中心的点被视 为噪声点。如果在图中给予一定范围的划分，比如像紫色部分中远离了中心部分的点像是最左 边下面的点被视为噪声点，可以使用相应的方法去掉这个噪声点。
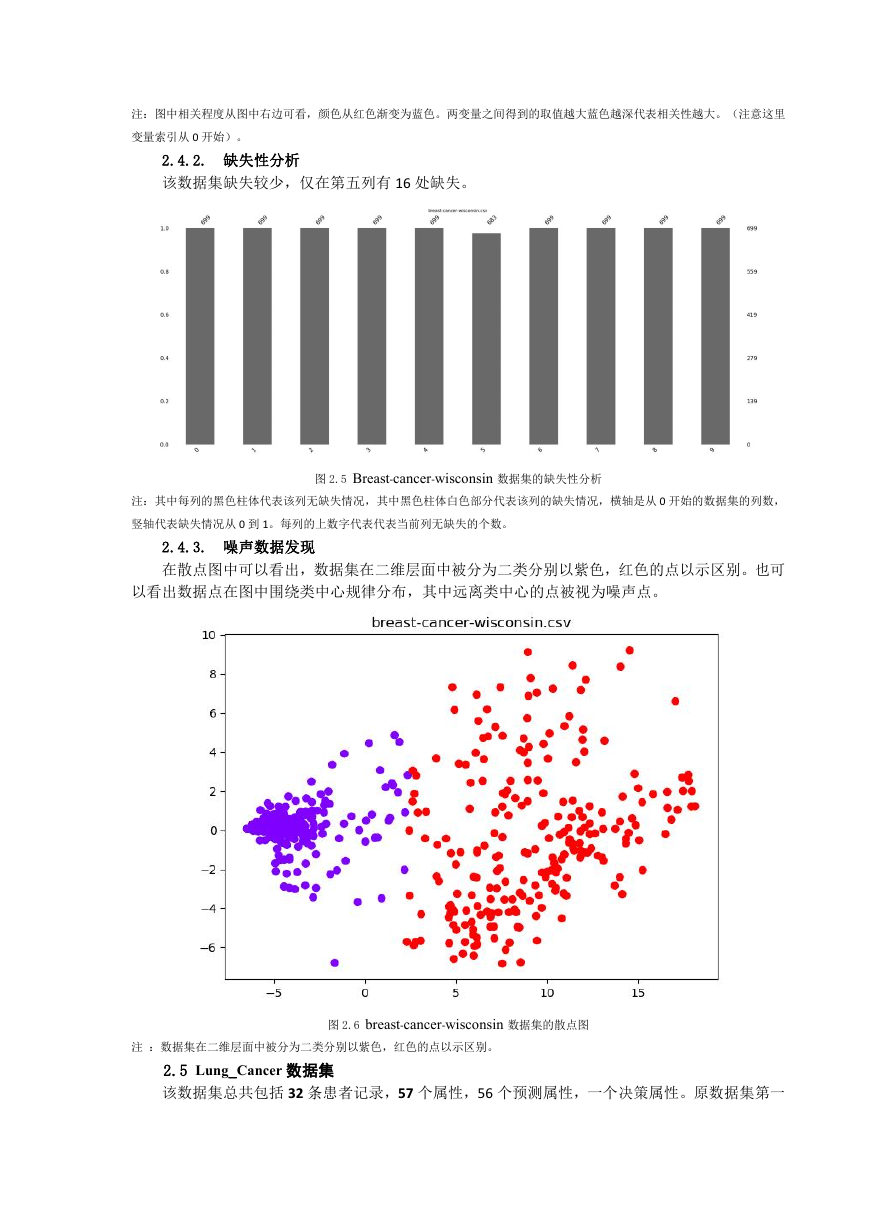
    图 2.3 Pima-indians-diabetes 数据集的散点图 注 ：数据集在二维层面中被分为三类分别以紫色，红色的点以示区别。 2.4 Breast-cancer-wisconsin 数据集： 这个乳腺癌区域是从大学医学中心获得的，总共有 699 条患者记录，10 个属性，其中属性包 括年纪，更年期，肿瘤大小等等，最后一列是决策属性，描述该记录是否患有乳腺癌。 2.4.1. 相关性分析 从图 2.4 中可以看出其中第 1 列和第 2 列相关性是最大的，第 8 列与其他列相关性都比较低。 整体上看，该数据集各列之间相关性一般。 图 2.4 Breast-cancer-wisconsin 数据集相关性图
    注：图中相关程度从图中右边可看，颜色从红色渐变为蓝色。两变量之间得到的取值越大蓝色越深代表相关性越大。（注意这里 变量索引从 0 开始）。 2.4.2. 缺失性分析 该数据集缺失较少，仅在第五列有 16 处缺失。 图 2.5 Breast-cancer-wisconsin 数据集的缺失性分析 注：其中每列的黑色柱体代表该列无缺失情况，其中黑色柱体白色部分代表该列的缺失情况，横轴是从 0 开始的数据集的列数， 竖轴代表缺失情况从 0 到 1。每列的上数字代表代表当前列无缺失的个数。 2.4.3. 噪声数据发现 在散点图中可以看出，数据集在二维层面中被分为二类分别以紫色，红色的点以示区别。也可 以看出数据点在图中围绕类中心规律分布，其中远离类中心的点被视为噪声点。 注 ：数据集在二维层面中被分为二类分别以紫色，红色的点以示区别。 图 2.6 breast-cancer-wisconsin 数据集的散点图 2.5 Lung_Cancer 数据集 该数据集总共包括 32 条患者记录，57 个属性，56 个预测属性，一个决策属性。原数据集第一
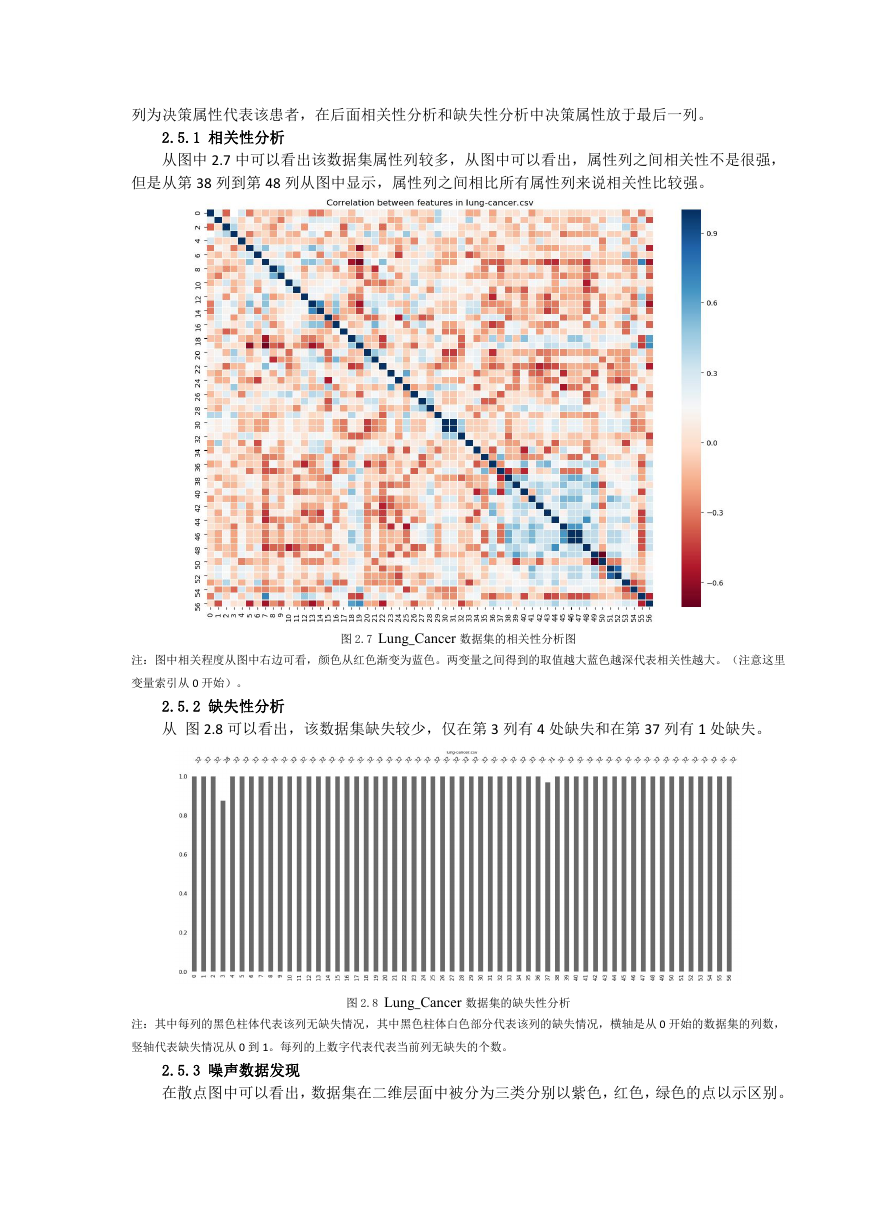
    列为决策属性代表该患者，在后面相关性分析和缺失性分析中决策属性放于最后一列。 2.5.1 相关性分析 从图中 2.7 中可以看出该数据集属性列较多，从图中可以看出，属性列之间相关性不是很强， 但是从第 38 列到第 48 列从图中显示，属性列之间相比所有属性列来说相关性比较强。 注：图中相关程度从图中右边可看，颜色从红色渐变为蓝色。两变量之间得到的取值越大蓝色越深代表相关性越大。（注意这里 图 2.7 Lung_Cancer 数据集的相关性分析图 变量索引从 0 开始）。 2.5.2 缺失性分析 从 图 2.8 可以看出，该数据集缺失较少，仅在第 3 列有 4 处缺失和在第 37 列有 1 处缺失。 图 2.8 Lung_Cancer 数据集的缺失性分析 注：其中每列的黑色柱体代表该列无缺失情况，其中黑色柱体白色部分代表该列的缺失情况，横轴是从 0 开始的数据集的列数， 竖轴代表缺失情况从 0 到 1。每列的上数字代表代表当前列无缺失的个数。 2.5.3 噪声数据发现 在散点图中可以看出，数据集在二维层面中被分为三类分别以紫色，红色，绿色的点以示区别。
    也可以看出数据点在图中围绕类中心规律分布，其中远离类中心的点被视为噪声点。 图 2.9 Lung_Cancer 数据集的散点图 注 ：数据集在二维层面中被分为三类分别以紫色，红色，绿色的点以示区别。 2.6 Risk_factors_cervical_Risk 数据集 数据集是在委内瑞拉加拉加斯的“加拉加斯大学医院”收集的。数据集包括 858 名患者的人口 统计信息、习惯和历史医疗记录。一些病人因为隐私问题(价值观缺失)而决定不回答其中的一些问 题。该数据集包括 858 条记录，36 个属性，35 个条件属性包括年纪，性伴侣个数，怀孕次数，吸 烟年龄等等，最后一列为决策属性代表该患者是否患有宫颈癌。 2.6.1 相关性分析： 从图中可以看出，该数据集属性列之间相关性不高，其中第 11 列，12 列，13 列之间相关性比 较高，整体上看该数据集属性之间相关性较低。
    分享到：
    赞 收藏

    相关推荐

    资料库

    人工智能

    共收录2047份资料，累计62个分类，关注成员有19位，主要包括：GNSS,Pico-SIM868-GSM,GPRS,NB-IoT,GPRSHAT,SIM7070GCat-M,GNSSHAT,GSM,NB-IoTHAT,SIM7080GCat-M,R800CGSM,SIM800CGSM,UPSPowerModule(B),UPSPowerModule,Pico-SIM7020C-NB-IoT,SIM7028NB-IoTHAT,SIM7020CNB-IoTHAT,SIM7000XNB-IoTHAT,A7670CCat-1HAT,A7600C1Cat-1,SIM7600X4G&LTECat-1HAT,SIM7600X4GDONGLE用户手册,RM520N-GL5GHAT,RM500Q-GL5GHAT,RM500U-CN5GHAT,SIM820X-M25GforJetsonNano,AudioCardforJetsonNano,SIM7600G-H4GforJetsonNano,OpenNCC-Lite-4G8M,IMX219-77Camera,13.3inche-PaperHAT,10.3inche-PaperHAT(D),10.3inche-PaperHAT,9.7inche-PaperHAT,7.8inche-PaperHAT,6inchHDTouche-PaperHAT,6inchHDe-PaperHAT,6inche-PaperHAT,5.83inche-PaperHAT(C),LCD-Clock-A,0.95inchRGBOLED(A),0.96inchRGBOLEDModule,0.96inchOLEDModule,0.96inchOLED(A),1.27inchRGBOLEDModule,1.3inchOLEDModule(C),1.3inchOLED(A),1.32inchOLEDModule,1.5inchRGBOLEDModule,1.5inchOLEDModule,JETSONORINNX,自然语言处理,搜索引擎,VR,计算广告,深度学习,机器学习

    热门标签

    GNSS Pico-SIM868-GSM GPRS NB-IoT GPRSHAT SIM7070GCat-M GNSSHAT GSM NB-IoTHAT SIM7080GCat-M R800CGSM SIM800CGSM UPSPowerModule(B) UPSPowerModule Pico-SIM7020C-NB-IoT SIM7028NB-IoTHAT SIM7020CNB-IoTHAT SIM7000XNB-IoTHAT A7670CCat-1HAT A7600C1Cat-1 SIM7600X4G&LTECat-1HAT SIM7600X4GDONGLE用户手册 RM520N-GL5GHAT RM500Q-GL5GHAT RM500U-CN5GHAT SIM820X-M25GforJetsonNano AudioCardforJetsonNano SIM7600G-H4GforJetsonNano OpenNCC-Lite-4G8M IMX219-77Camera 13.3inche-PaperHAT 10.3inche-PaperHAT(D) 10.3inche-PaperHAT 9.7inche-PaperHAT 7.8inche-PaperHAT 6inchHDTouche-PaperHAT 6inchHDe-PaperHAT 6inche-PaperHAT 5.83inche-PaperHAT(C) LCD-Clock-A 0.95inchRGBOLED(A) 0.96inchRGBOLEDModule 0.96inchOLEDModule 0.96inchOLED(A) 1.27inchRGBOLEDModule 1.3inchOLEDModule(C) 1.3inchOLED(A) 1.32inchOLEDModule 1.5inchRGBOLEDModule 1.5inchOLEDModule JETSONORINNX 自然语言处理 搜索引擎 VR 计算广告 深度学习 机器学习

    最新资料