GCN-PPT.pptx

发布时间：2022-06-19 发布人：admin 分类：说明书资料大小：1.28M 资料格式：pptx 举报版权申诉

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第1页.png

第1页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第2页.png

第2页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第3页.png

第3页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第4页.png

第4页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第5页.png

第5页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第6页.png

第6页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第7页.png

第7页 / 共12页

9adee470-fe1f-4a0c-aa7a-d25c5ad333a7.pptx.pdf-第8页.png

第8页 / 共12页

文本预览

GCN介绍与工作汇报汇报人：sendy.lee 2019.12.13

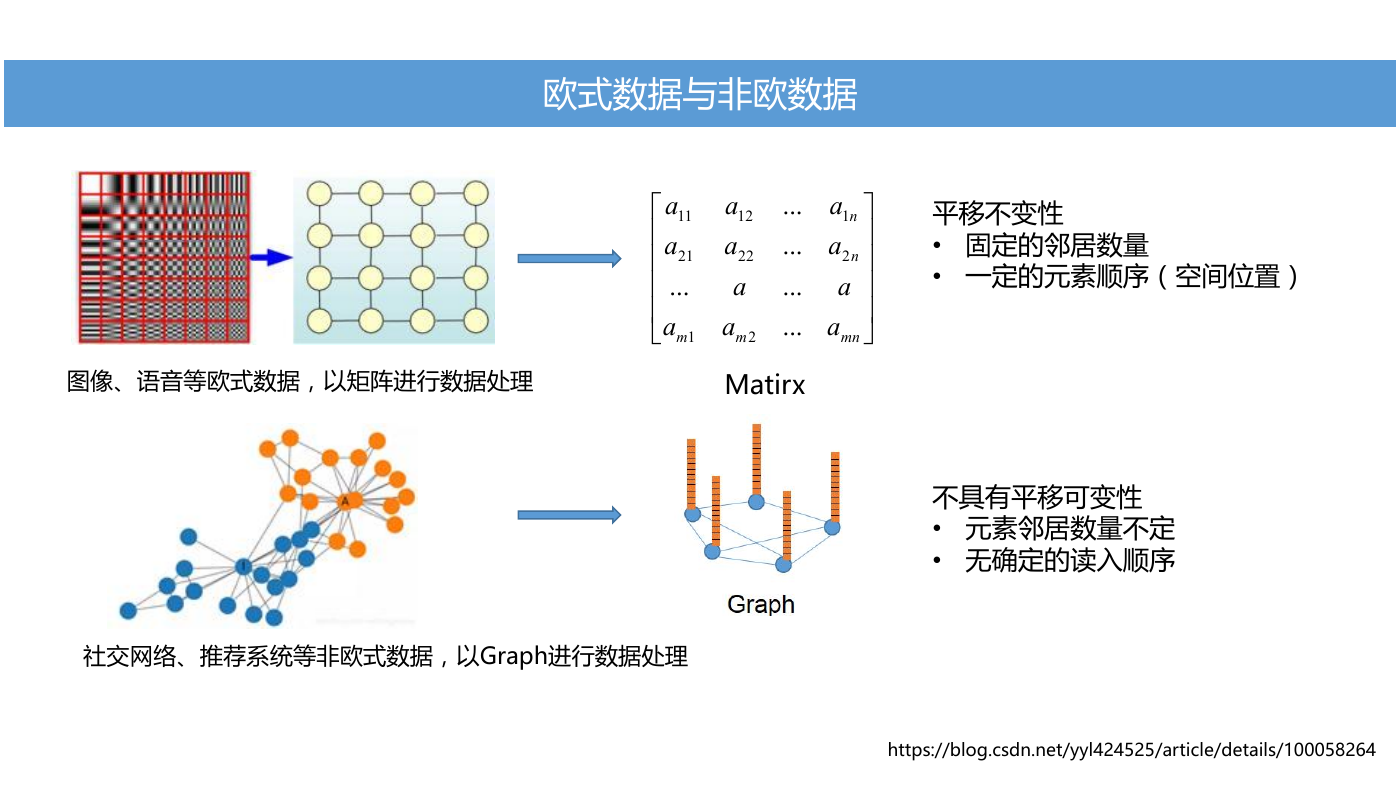
欧式数据与非欧数据 a 11 a 21 ... a 1 m       a 12 a 22 a a m 2 ... ... ... ... a 1 n a 2 n a a mn       平移不变性 • 固定的邻居数量 • 一定的元素顺序（空间位置）图像、语音等欧式数据，以矩阵进行数据处理 Matirx 社交网络、推荐系统等非欧式数据，以Graph进行数据处理不具有平移可变性 • 元素邻居数量不定 • 无确定的读入顺序 https://blog.csdn.net/yyl424525/article/details/100058264

GCN来源 original image和shuffled后的图像，其像素点的像素值并没有发生变化，图中信息（秃鹫/老鹰）却丢失了 • 元素读入顺序含有大量信息但Graph无天然顺序 CNN对欧式数据处理方式：随机初始化一定尺寸的卷积核，进行加权求和，经过BP算法优化，获得最适合任务的“权值” GCN思路与此相同，因此需要设计获得可优化的卷积核参数 https://blog.csdn.net/weixin_43279911/article/details/103496532

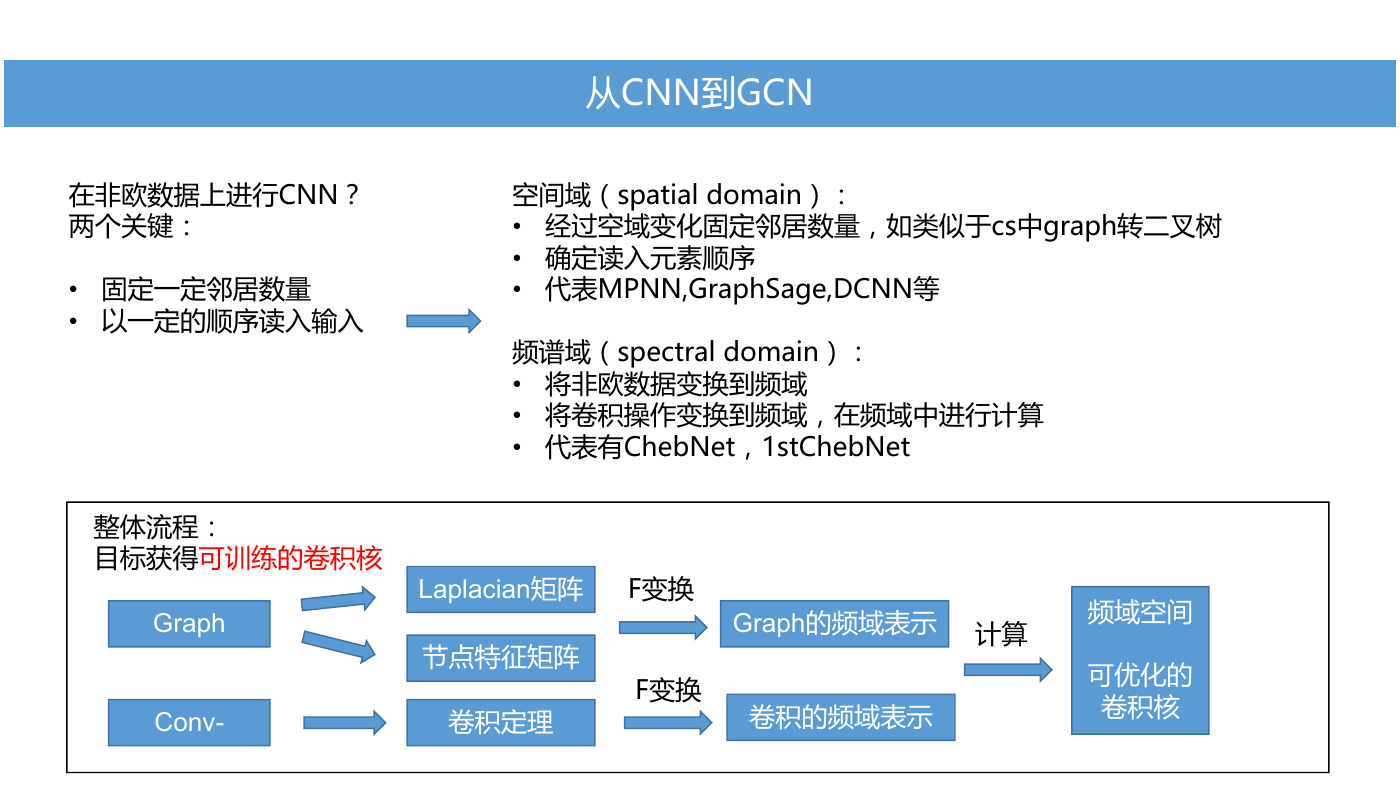
在非欧数据上进行CNN？两个关键： • 固定一定邻居数量 • 以一定的顺序读入输入整体流程：目标获得可训练的卷积核 Graph Conv- 从CNN到GCN 空间域（spatial domain）： • 经过空域变化固定邻居数量，如类似于cs中graph转二叉树 • 确定读入元素顺序 • 代表MPNN,GraphSage,DCNN等频谱域（spectral domain）： • 将非欧数据变换到频域 • 将卷积操作变换到频域，在频域中进行计算 • 代表有ChebNet，1stChebNet Laplacian矩阵 F变换 Graph的频域表示计算节点特征矩阵卷积定理 F变换卷积的频域表示频域空间可优化的卷积核

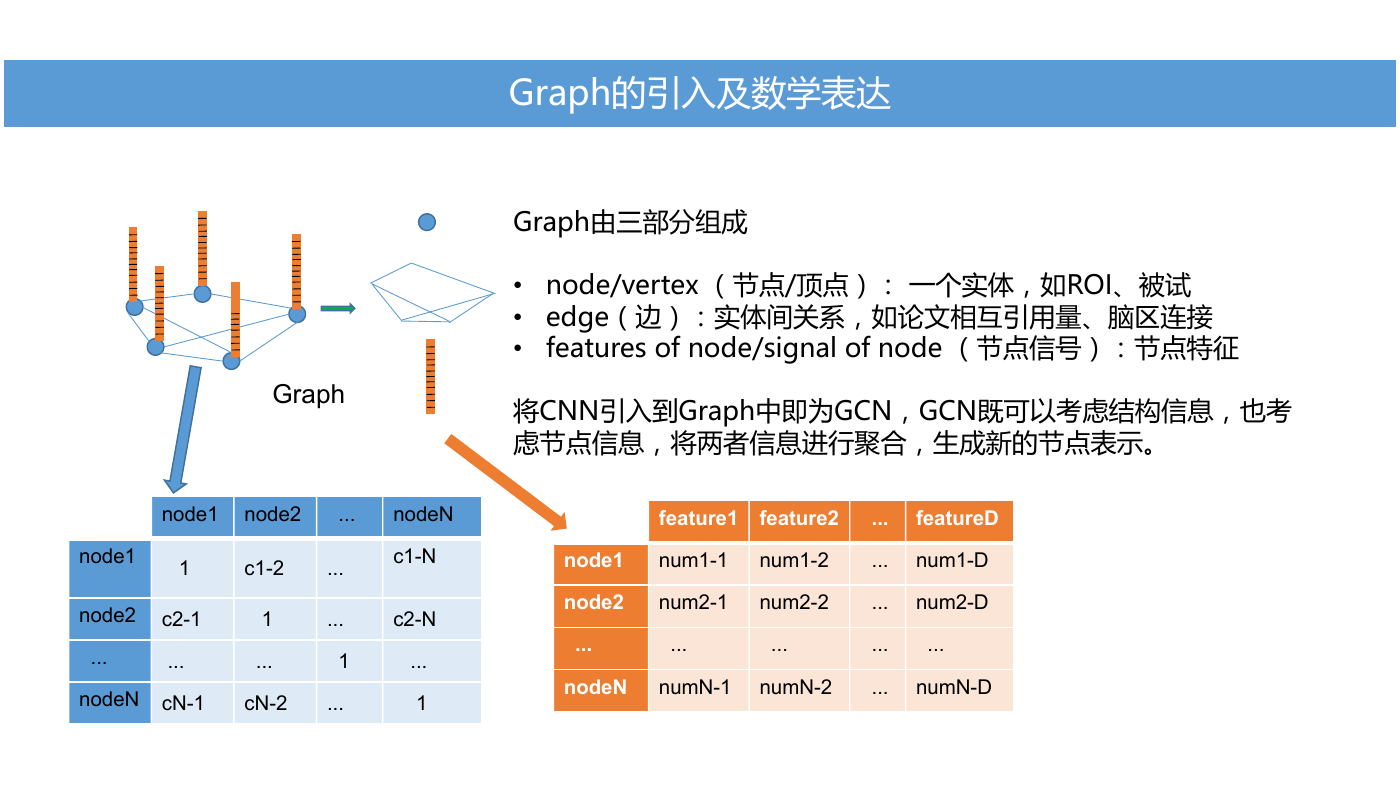
Graph的引入及数学表达 Graph由三部分组成 Graph • node/vertex （节点/顶点）：一个实体，如ROI、被试 • edge（边）：实体间关系，如论文相互引用量、脑区连接 • features of node/signal of node （节点信号）：节点特征将CNN引入到Graph中即为GCN，GCN既可以考虑结构信息，也考虑节点信息，将两者信息进行聚合，生成新的节点表示。 node1 node2 ... nodeN node1 1 c1-2 node2 c2-1 ... ... nodeN cN-1 1 ... cN-2 ... ... 1 ... c1-N c2-N ... 1 feature1 feature2 ... ... num1-1 num1-2 num2-1 num2-2 ... ... numN-1 numN-2 ... ... ... featureD num1-D num2-D ... numN-D node1 node2 ... nodeN

Graph的表示--Laplacian矩阵  AD Laplacian matrix是图论中对图的矩阵形式表示，定义为： ADL  2/1 sys  L （对称归一化的 Laplacian） DI  2/1  LD  D  2/1  2/1  AD 其中A为邻接矩阵，D表示为度矩阵值得注意的是： 1.邻接矩阵A有且仅有k-hop有数值 2.拉普拉斯矩阵中在对角线和k-hop处有值 https://blog.csdn.net/weixin_43279911/article/details/103496532

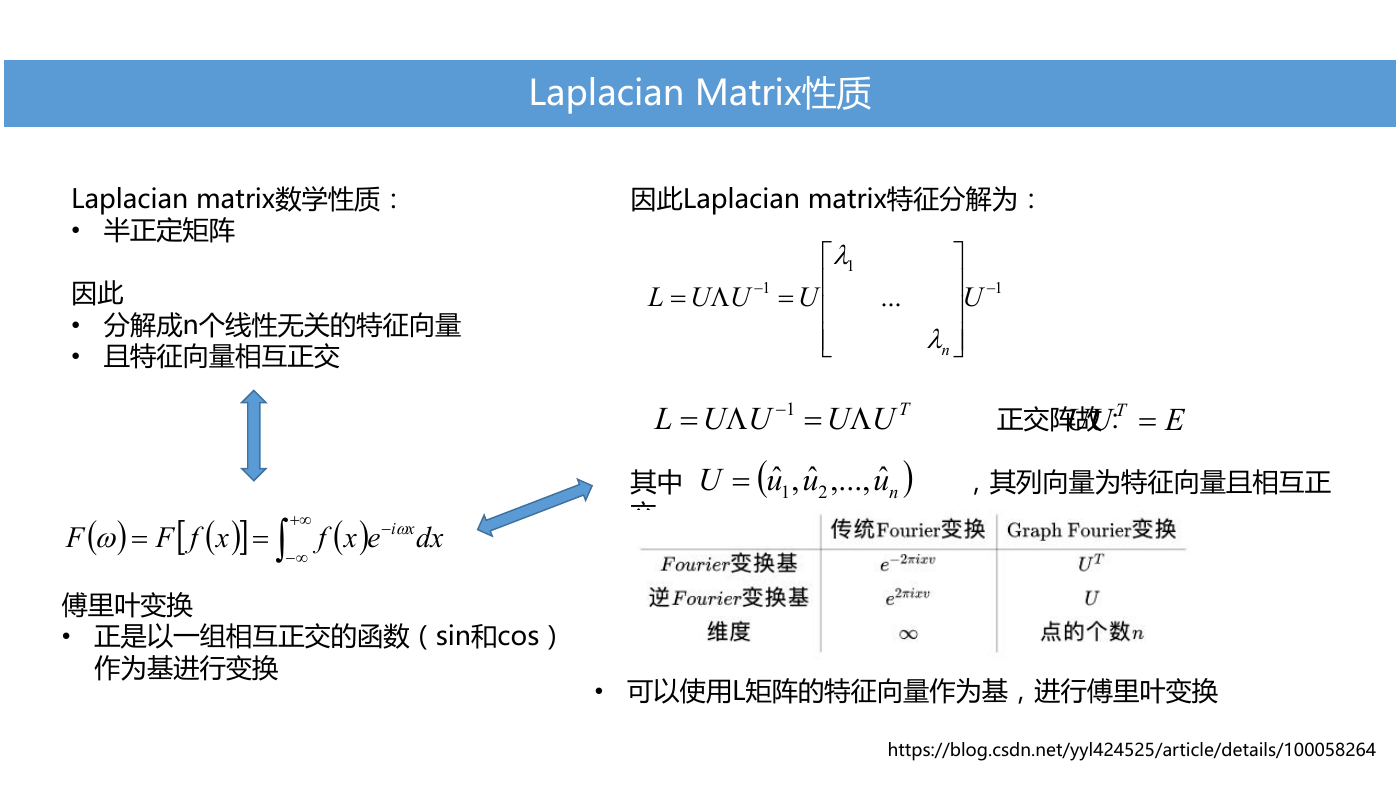
Laplacian Matrix性质 Laplacian matrix数学性质： • 半正定矩阵因此 • 分解成n个线性无关的特征向量 • 且特征向量相互正交因此Laplacian matrix特征分解为： UUL  1   U   1     ... 1    U    n    F      xfF      exf  xi dx 傅里叶变换 • 正是以一组相互正交的函数（sin和cos）作为基进行变换 1 UUL  1  ˆ,ˆ uuU 2 TUU  nu ˆ ,..., 正交阵故： UU T  E 其中，其列向量为特征向量且相互正交 • 可以使用L矩阵的特征向量作为基，进行傅里叶变换 https://blog.csdn.net/yyl424525/article/details/100058264

Graph傅里叶变换得到Graph傅里叶变换及反变换形式 F    l  ˆ    f l  N  i 1      iuif l   if  N  i 1  ˆ      f iu l l • 其中为节点特征 /节点信号，为特征向量分量  if  iul 矩阵形式： ˆ f ˆ f ... ˆ f           1    2   N                u 1 u   1   1 2 ...   1 N u u 1 u   2   2 2 ...   2 u N ... ... ... ...  Nu 1  Nu 2 ...  Nu N      1   2 f f ...  Nf                     1   2 f f ...  Nf                 1 u 1   2 u 1 ...  Nu 1        2 u u   1   2 2 ...  Nu 2  ... ... ... ... N u u   1   2 N ...  Nu N  ˆ f ˆ f ... ˆ f                 1    2   N        https://blog.csdn.net/yyl424525/article/details/100058264

分享到：

赞收藏

资料库

GCN-PPT.pptx

相关推荐

人工智能

热门标签

最新资料